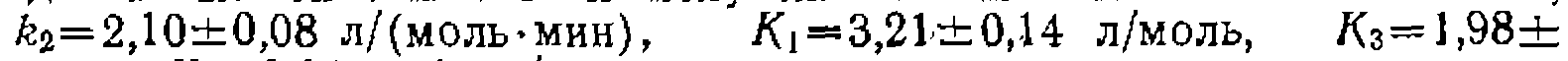|
|
КИНЕТИКА МЕТАЛЛОКОМПЛЕКСНОГО КАТАЛИЗАОсновными отличиями рассмотренных выше схем реакций металлокомплексного катализа от других гомогенно-каталитических реакций являются миогостадийность н большое число комплексов, содержащих металл-каталнзатор. В качестве лигандов такие комплексы включают реагенты, продукты их промежуточных превращений, продукты реакции и присутствующие в реакционной массе комплексообразующие вещества или анионы. В общем случае подробно рассмотренная выше схема нуклеофильного катализа (111-2) дополняется равновесиями комплек- сообразования с перечисленными лигандами в разных сочетаниях. На примере нескольких типичных равновесий, дополняющих схему нуклеофильного катализа, проанализируем вид отвечающих ей кинетических уравнений и рассмотрим методы экспериментального определения параметров этих уравнений и проверки их адекватности. Возьмем за основу схему металлокомплексного катализа реакции A+Y—протекающей через стадии последовательного ввода реагентов А и Y в координационную сферу комплекса металла М, мономолекулярного превращения образовавшегося комплекса
Здесь символом М обозначен комплекс металла с лигандами, которые не диссоциируют и не обмениваются в ходе .реакции, a Xt и Хг — промежуточные комплексы, содержащие в качестве лигандов исходные реагенты или продукты их превращений (например, X] может быть продуктом окислительного присоединения водорода к М и т. п.). Выведем кинетическое уравнение для условий избытка одного из реагентов
Для принятого соотношения концентраций реагентов и катализатора концентрации свободных реагентов и лиганда равны иханалитически определяемым концентрациям
Используя это уравнение н уравнения для констант равновесия, легко выразить концентрацию любого комплекса металла через концентрации реагентов и или
Последнее выражение носит название функции закомплексованности катализатора свободного комплекса
в значительной степени связан в комплексы с разными лигандами. Используя
Подставив ее в (111-46), получим выражение для скорости реакции:
Полученное уравнение легко приводится к стандартному виду, использованному ранее для описания кинетики нуклеофильного катализа
со значениями
В разделе нуклеофильного катализа описаны интегральный и дифференциальные методы проверки адекватности такого уравнения и определения параметров В соответствии с этим в координатах сти уравнения (111-49) эксперименту должна быть получена одна прямая линиядля всех начальных концентраций При варьировании избытка L -по отношению к
рии экспериментов с варьированием избытка С’у,о >по отношению к СА)о получается пучок прямых, пересекающихся в точке с координатами В практике исследования кинетики реакций металлокомплексного катализа все слагаемые знаменателя уравнения (111-48)—функции закомплексованности — относительно редко сравнимы с единицей. Обычно концентрации некоторых комплексов малы, и соответствующими слагаемыми можно пренебречь. В частности, при очень малой степени диссоциации комплекса ML наибольшее значение имеет слагаемое
Кинетические кривые при этом условии описываются уравнением первого порядка, экспериментально определяемая константа скорости пропорциональна Большое значение константы равновесия
При достаточно оольшом изоытке; практически весь катализатор связывается в комплекс Обратное соотношение этих величин знаменателя уравнения (111-48) долю связывания металла в комплекс
Возможны и другие соотношения слагаемых функции закомплексованности, которые приводят к иным частным варианта^ общего кинетического уравнения (111-48). Наличие равновесных реакций, в которых образуются другие комплексы, содержащие металл, наоборот, приводит ,к усложнению уравнения (111-48) и появлению новых членов в функции закомплексованности. В качестве примеров можно привести часто встречающееся ингибирование продуктом реакции, которое проявляется в образовании комплекса .продукта с катализатором в исходной форме М или в форме промежуточного комплекса с исходным реагентом
Возможно также ингибирование исходным реагентом в результате образования неактивного комплекса Ингибирование продуктом реакции до равновесию (а) приводит к появлению в знаменателе уравнения (Ш-48) нового члена
Ингибирование реакции по равновесиям (б) и (в) поиводит к появлению в знаменателе квадратичных членов
уравнение приводится к виду
и зависимость Са от t не линеаризуется описанными выше методами. Для определения параметров уравнения (Ш-51) можно преобразовать его интегральную форму к следующему линейному виду относительно определяемых параметров
или воспользоваться нелинейными методами наименьших квадратов. Приведенный кинетический анализ не исчерпывает всех видов уравнений, встречающихся при металлокомплексном катализе, и касается лишь наиболее распространенных их форм. Более сложные уравнения возможны при многом.аршрутном пути образования конечных продуктов, при сравнимых скоростях образования промежуточных комплексов и их последующих превращений, при необратимых превращениях катализатора в другие формы в ходе реакции и т. п. Изложение этих вопросов выходит, однако, за рамки данного курса. Пример. Реакцию элоксидирования циклогексека гндропероксидом этил- бензола
изучали в растворе этилбензола. В качестве катализатора иснользовали гли- колят молибдена убыли гидроперокеида (А) в избытке циклогексена (Y). В серии опытов при концентрациях концентрациях С’а, о нолучены следующие результаты:
Для построения кинетического уравнения и определения механизма реакции нрименяем предварительный анализ данных по начальным скоростям,, являющийся разновидностью дифференциального метода обработки опытов. Для этого графическим дифференцированием кривых ( ж ' нахо
дим начальные скорости реакции, которые равны соответственно 0,0025,. 0,0042, 0,0048 и 0,0057 моль/(л-мии). Полученная зависимость г0 от СА, о спрямляется в координатах нию и Кинетические опыты нри варьировании С\, 0 и прим.оль/л и
Начальныескорости в опытах № 2, 5 и 6, различающихся только концентрациями 0, 0014 моль/(л-мин). График в координатах
Начальные скорости в опытах № 7, 2 и 8, различающихся только концентрациями катализатора, равны соответственно 0,0020, 0,0042 и 0, 0060 моль/(л-мин). Так же как и в предыдущейсерии экснеримеитов, получается линейная зависимость в координатах
Графическим дифференцированием находим следующие значения начальных скоростей: С целью выяснения влияния продуктов реакции на скорость были нро- ведены две серии онытовс добавками В иZ в исходную смесь реагентов при
Как видно из полученных данных, оба продукта тормозят реакцию [начальная скорость в этих же условиях, ио без добавления продуктов (опыт № 2) составляет тов вместе с опытом № 2 в координатах дает прямые, отсекающие и а оси ор дипат один и тот же отрезок. Полученные результаты свидетельствуют о том, что катализатор образует с гидропероксидом активный промежуточнвш комплекс, а с оксидом и спиртом — неактивные комплексы, тормозящие реакцию. Этому соответствует такой механизм
и следующее кинетическое уравнение:
Для окончательной нроверки адекватности уравнения обрабатываем весь массив данных по временным зависимостям го интегрирования и ноиска констант при помощи нелинейного М.НК. При этом значения констант, найденные в результате предварительной обработки кинетического эксперимента по начальным скоростям, были использованы в качестве начальных нриближений. Уточненные значения нараметров, обеснечи- вающне адекватные описания всех нолученных кинетических зависимостей, равны: 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 в продукт реакции Р и равновесия комплексообразования металла с диссоциирующим лигандом L:
в продукт реакции Р и равновесия комплексообразования металла с диссоциирующим лигандом L: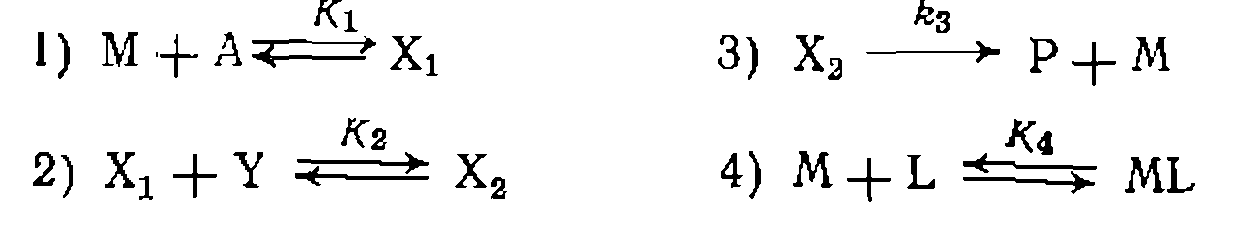
 и низкой суммарной концентрации комплексов металла по сравнению с концентрациями реагентов и лиганда
и низкой суммарной концентрации комплексов металла по сравнению с концентрациями реагентов и лиганда  . Эти условия обычно легко достижимы и существенно упрощают внд кинетического уравнения, а также его последующее использование для обработки экспериментальных данных. Предположим также, что все равновесия устанавливаются быстро, а лимитирующей стадией является превращение
. Эти условия обычно легко достижимы и существенно упрощают внд кинетического уравнения, а также его последующее использование для обработки экспериментальных данных. Предположим также, что все равновесия устанавливаются быстро, а лимитирующей стадией является превращение  . Скорость реакции при этом описывается уравнением
. Скорость реакции при этом описывается уравнением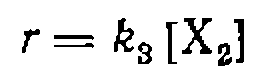 (III-46)
(III-46)
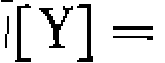

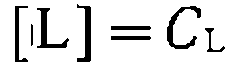 , а исходная концентрация катализатора См представляет собой сумму концентраций всех комплексов, содержащих металл:
, а исходная концентрация катализатора См представляет собой сумму концентраций всех комплексов, содержащих металл: 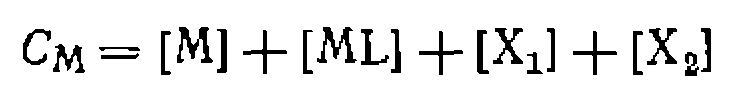
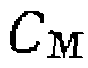
 (III-47)
(III-47) . Каждый член этого выражения представляет собой долю металла, связанного с соответствующим лигандом _ __
. Каждый член этого выражения представляет собой долю металла, связанного с соответствующим лигандом _ __  по отношению к концентрации
по отношению к концентрации . Значение
. Значение 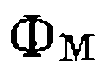 изменяется от единицы, когда концентрации всех комплексов малы по сравнению си
изменяется от единицы, когда концентрации всех комплексов малы по сравнению си  , до сколь угодно большой величины, когда М
, до сколь угодно большой величины, когда М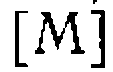
 , легко выразить концентрациюлюбого комплекса через суммарную концентрацию металла
, легко выразить концентрациюлюбого комплекса через суммарную концентрацию металла 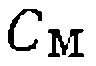 и кон- центрацнн реагентов. В частности, входящая в кинетическое уравнение (III-46) концентрация
и кон- центрацнн реагентов. В частности, входящая в кинетическое уравнение (III-46) концентрация  равна:
равна: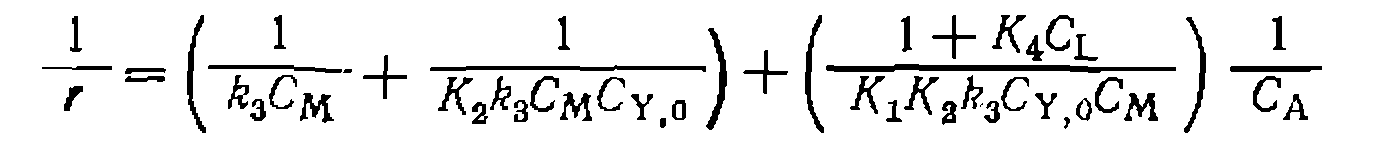
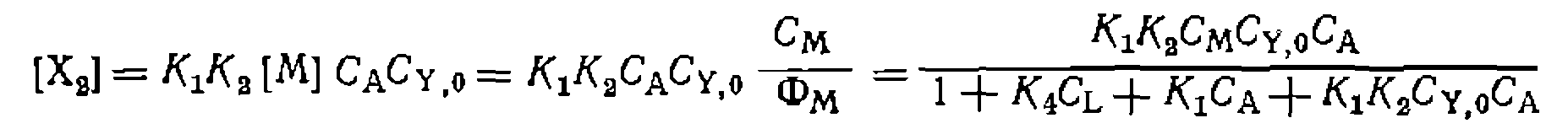
 (111-48)
(111-48) (111-49)
(111-49) и
и 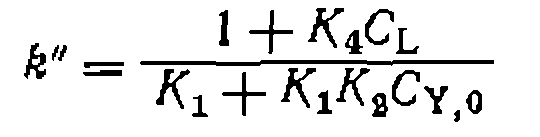
 и
и  из кинетических зависимостей
из кинетических зависимостей  от t. Серии кинетических экспериментов с варьируемыми значениями
от t. Серии кинетических экспериментов с варьируемыми значениями  и
и  позволяют определить также и всевходящие в
позволяют определить также и всевходящие в  и
и 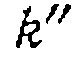 значения констант равновесия
значения констант равновесия 
 и
и  и константы скорости
и константы скорости  , В частности, преобразование уравнения (111-49) в координатах Лайнуивера — Берка при дифференциальном методе обработки кинетических кривых дает:
, В частности, преобразование уравнения (111-49) в координатах Лайнуивера — Берка при дифференциальном методе обработки кинетических кривых дает: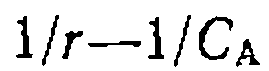 при адекватно
при адекватно при постоянстве
при постоянстве 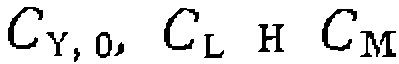
 и при постоянстве всех других начальных концентраций получается пучок прямых, пересекающих ось ординат в точке
и при постоянстве всех других начальных концентраций получается пучок прямых, пересекающих ось ординат в точке 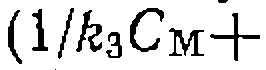
 и имеющих тангенс угла наклона, линейно гюл- растающий с концентр ап ней L
и имеющих тангенс угла наклона, линейно гюл- растающий с концентр ап ней L 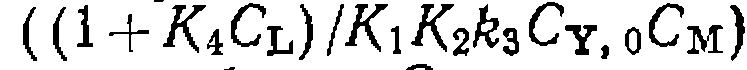 .В се
.В се Тангенс угла наклона этих прямых и отрезки, отсекаемые на оси ординат,, обратно пропорциональны
Тангенс угла наклона этих прямых и отрезки, отсекаемые на оси ординат,, обратно пропорциональны 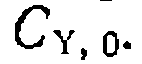
 При этом практически весь катализатор находится в форме ML
При этом практически весь катализатор находится в форме ML  , и уравнение (111-48) приобретает вид:
, и уравнение (111-48) приобретает вид: (III-50)
(III-50) и
и  и обратно пропорциональна
и обратно пропорциональна  , а кинетический эксперимент позволяет определить только комбинацию констант скорости н равновесия
, а кинетический эксперимент позволяет определить только комбинацию констант скорости н равновесия  Уравнение (111-48) можно привести к этому виду н путем выбора условий эксперимента, обеспечив достаточно большой избыток
Уравнение (111-48) можно привести к этому виду н путем выбора условий эксперимента, обеспечив достаточно большой избыток  при относительно невысоких концентрациях
при относительно невысоких концентрациях  и
и 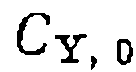
 по сравнению с
по сравнению с и
и  приводит к преимущественному образованию комплекса Xi
приводит к преимущественному образованию комплекса Xi  При этом условии кинетическое уравнение (III-48) переходит в уравнение нулевого порядка по А:
При этом условии кинетическое уравнение (III-48) переходит в уравнение нулевого порядка по А: (ГП-51)
(ГП-51) f
f  велика или
велика или 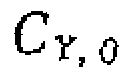 в
в и скорость реакции не зависит от концентраций обоих реагентов, а определяется только концентрацией катализатора
и скорость реакции не зависит от концентраций обоих реагентов, а определяется только концентрацией катализатора 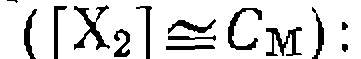
 (111-52)
(111-52)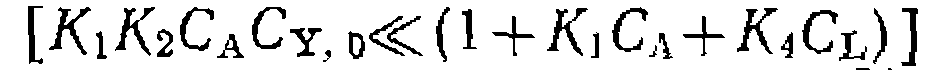 озн алает очень малую
озн алает очень малую или отсутствие равновесной стадии его образования и прямую реакцию Хн-Y—+ +М. Кинетическое уравнение в этом случае имеет вид:
или отсутствие равновесной стадии его образования и прямую реакцию Хн-Y—+ +М. Кинетическое уравнение в этом случае имеет вид: (111-53)
(111-53)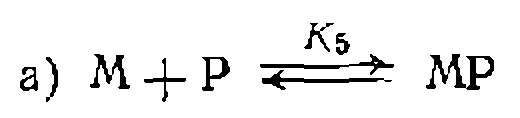
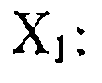
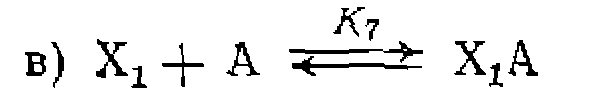
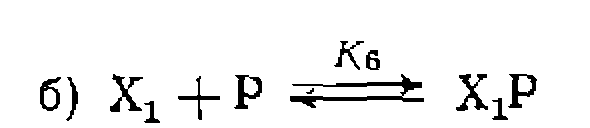
 с А:
с А: , что не меняет, однако, общего вида зависимости СА от t, которая описывается уравнениями
, что не меняет, однако, общего вида зависимости СА от t, которая описывается уравнениями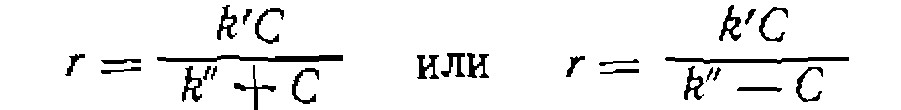
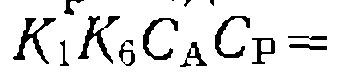
 В этих случаях кинетическое
В этих случаях кинетическое (III-64)
(III-64)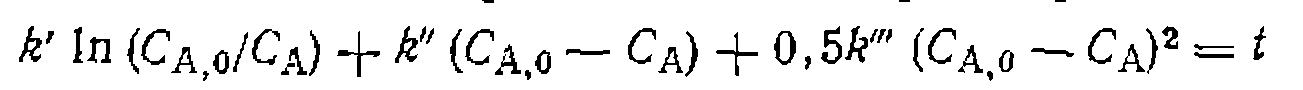

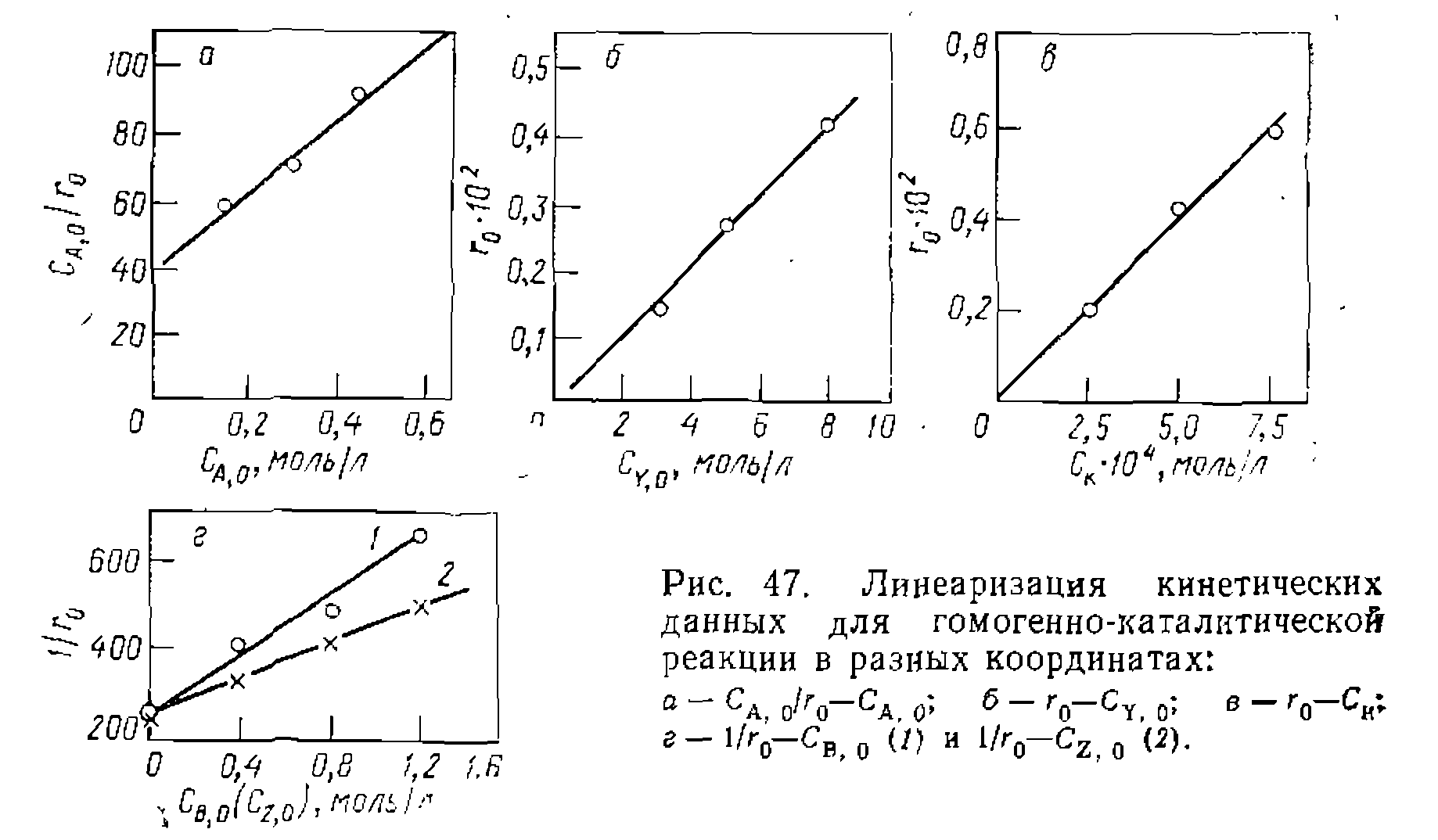
 За скоростью реакции следили по
За скоростью реакции следили по моль/л и различных начальных
моль/л и различных начальных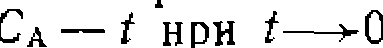
 (Рис- 47, еЛ. что отвечает уравне
(Рис- 47, еЛ. что отвечает уравне со значениями констант
со значениями констант 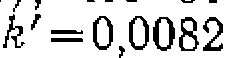 моль/(л-мин)
моль/(л-мин)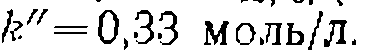
 моль/л дали следующие результаты:
моль/л дали следующие результаты: 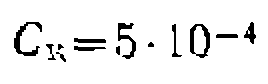
 (8, 5 и 3 моль/л соответственно), равны 0,0042, 0,0027 и
(8, 5 и 3 моль/л соответственно), равны 0,0042, 0,0027 и (рис. 47,6) дает прямую, выходящую из начала координат, что свидетельствует о первом порядке реакции по реагенту Y и отсутствии Су в функции закомплексованности. Серия кинетических опытов при разных концентрациях катализатора, = 8 моль/л и
(рис. 47,6) дает прямую, выходящую из начала координат, что свидетельствует о первом порядке реакции по реагенту Y и отсутствии Су в функции закомплексованности. Серия кинетических опытов при разных концентрациях катализатора, = 8 моль/л и  =0,3 моль/л, дала следующие результаты:
=0,3 моль/л, дала следующие результаты: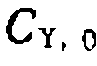
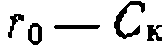 , свидетельствующая о первом порядке по катализатору (рис. 47, б).
, свидетельствующая о первом порядке по катализатору (рис. 47, б).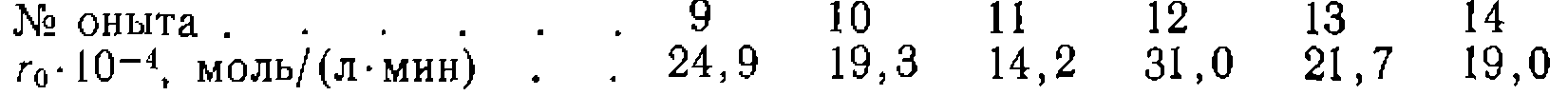
 =5-10-^ моль/л,
=5-10-^ моль/л,  =0,3 моль/л и
=0,3 моль/л и  =8,0 моль/л:
=8,0 моль/л: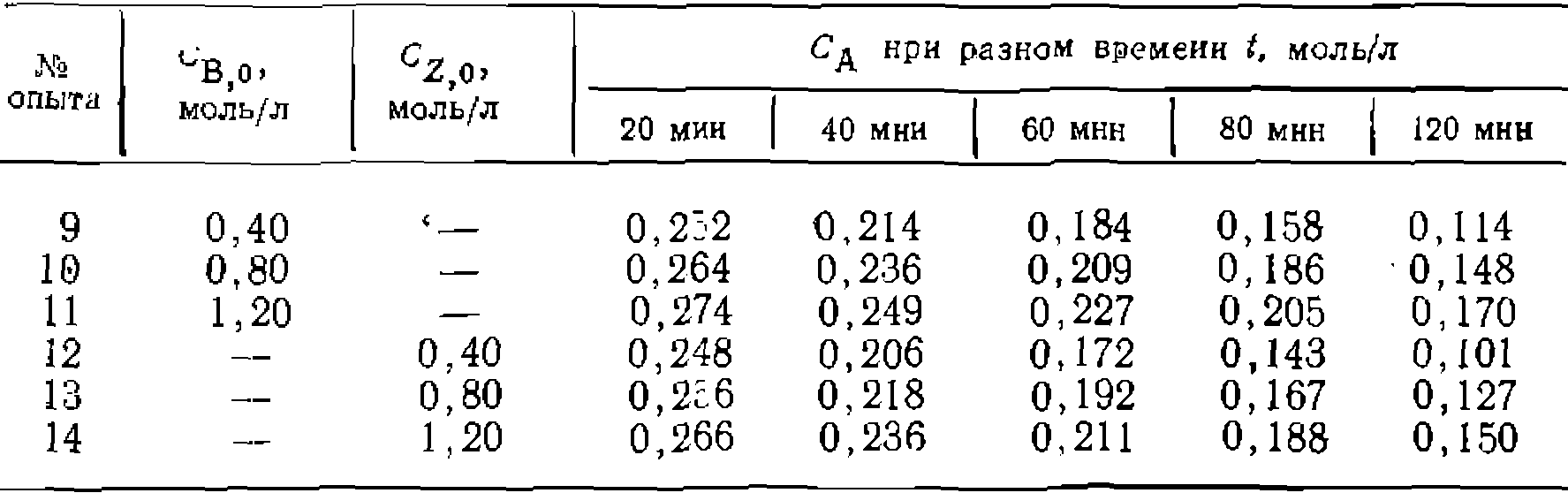
 моль/(л-мии)]. Обработка последней серии эксперимен
моль/(л-мии)]. Обработка последней серии эксперимен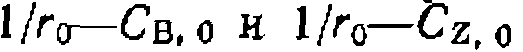 (рис. 47, г)
(рис. 47, г)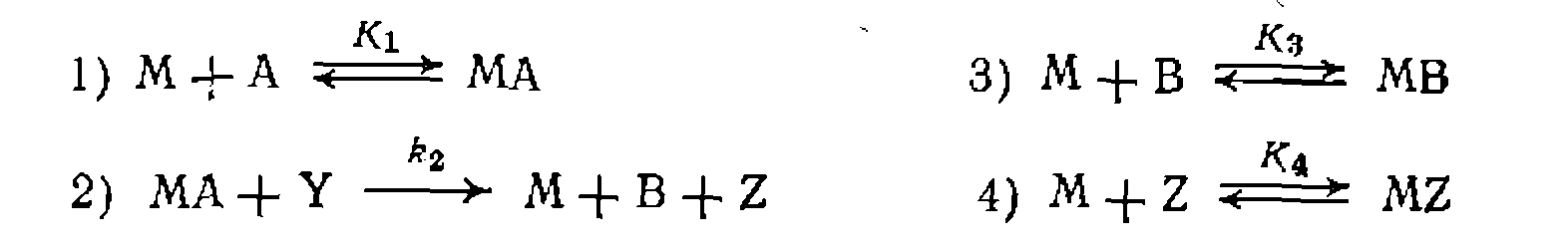
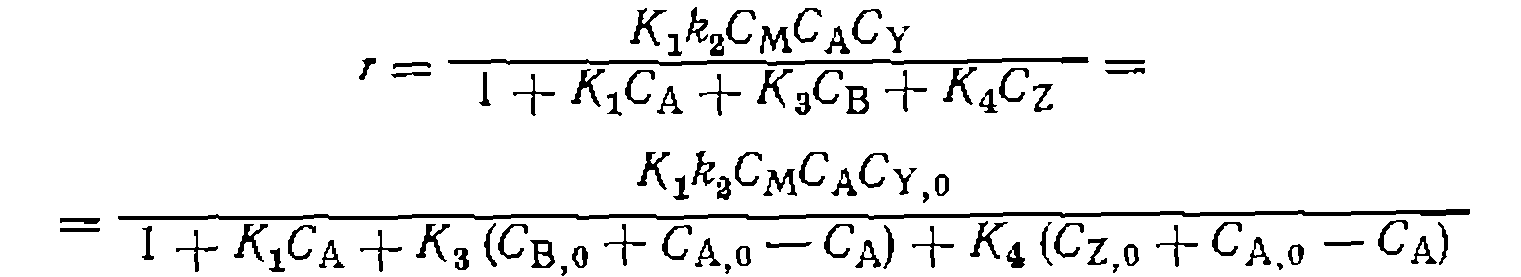
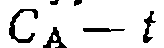 на ЭВМ нутем численно
на ЭВМ нутем численно