
|
|
Дисперсия воспроизводимости в этой функции будет равна
-Это меньше его табличного значения—19,38, что свидетельствует об адекватности уравнения опыту. Находим среднюю квадратичную ошибку в константе:
-Это меньше его табличного значения—19,38, что свидетельствует об адекватности уравнения опыту. Находим среднюю квадратичную ошибку в константе:
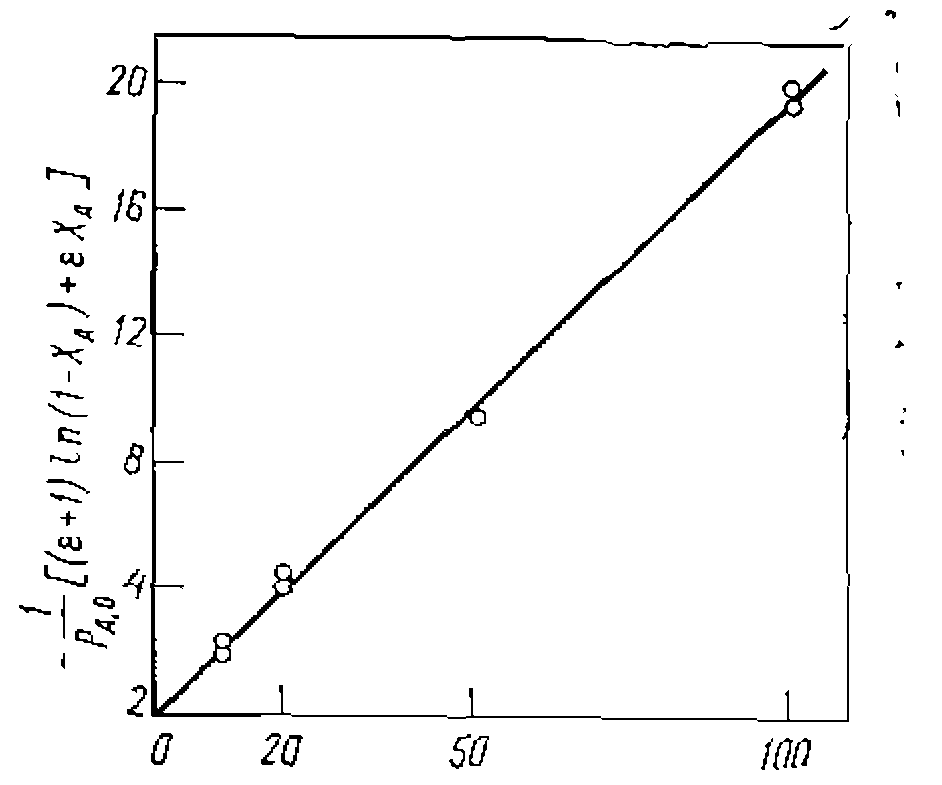
Рис. 17. Линеаризация опытов при интегральной обработке кинетических данных для реакции первого порядка, изучаемой в периодических условиях. Ее доверительный интервал . Отбрасывая лишние значащие цифры в найденной величине, приходим к кинетическому уравнению:
При игпппмпвяи™ пелипейного МНК также строим графическую зависимость
Ее доверительный интервал . Отбрасывая лишние значащие цифры в найденной величине, приходим к кинетическому уравнению: При игпппмпвяи™ пелипейного МНК также строим графическую зависимость и предварительно убеждаемся в вероятности принятой гипотезы. После этого по тангенсу угла наклона прямой на рис. 17 приблизительно оцениваем величину константы скорости. Положим, что оиа получилась равной 0,046. Преобразуем интегральный вид уравнения в форму,. разрешенную относительно , и рассчитываем на цифровой ЭВМ для каждой экспериментальной точки значения н
Оказывается, что минимум суммы квадратов отклонений находится при
г. е. раметром равна дисперсии адекватности, умноженной на обратную величину вторых производных минимизируемой функции по этому параметру
Оказывается, что минимум суммы квадратов отклонений находится при , составляя 1,8-10-4. Дисперсия адекватности . что дает критерий Фишера, равный I, г. е. . Дисперсия константы для уравнения с одним неизвестным па раметром равна дисперсии адекватности, умноженной на обратную величину вторых производных минимизируемой функции по этому параметру . В данном, случае получим
и доверительный интервал константы равен:
В результате получаем кинетическое уравнение:
В результате получаем кинетическое уравнение:
Значение константы получилось немного иное, чем- при линейном- МНК> который дал смещенную оценку ее величины: Необратимые простые реакции в условиях идеального вытеснения (в потоке). Поскольку этот метод исследования кинетики применяют преимущественно для газофазных реакций, часто идущих с изменением объема, то независимой переменной наиболее удобно выбрать степень конверсии основного реагента Ха, а для учета изменения объема — коэффициент его изменения е. Тогда кинетическое уравнение для необратимой простой реакции будет выглядеть так: Значение константы получилось немного иное, чем- при линейном- МНК> который дал смещенную оценку ее величины: Необратимые простые реакции в условиях идеального вытеснения (в потоке). Поскольку этот метод исследования кинетики применяют преимущественно для газофазных реакций, часто идущих с изменением объема, то независимой переменной наиболее удобно выбрать степень конверсии основного реагента Ха, а для учета изменения объема — коэффициент его изменения е. Тогда кинетическое уравнение для необратимой простой реакции будет выглядеть так:
где
Рис. 18. Линеаризация опытов при интегральной обработке кинетических данных для газофазной реакции первого порядка, изучаемой в условиях идеального вытеснения. Рис. 18. Линеаризация опытов при интегральной обработке кинетических данных для газофазной реакции первого порядка, изучаемой в условиях идеального вытеснения. Этот общий вид уравнения и его интегральное решение часто упрощаются при , и в других частных случаях. Некоторые из наиболее распространенных примеров решений приведены в табл. 10. Здесь предварительная npoi опытом также проводится путе: левой части уравнения против . Поиск KOIH проводят по минимуму суммы конверсии
Этот общий вид уравнения и его интегральное решение часто упрощаются при верка соответствия уравнения с м линеаризации в координатах условного времени контакта гстанты по нелинейному МНК квадратов отклонений в степени Здесь предварительная проверка соответствия уравнения с опытом также проводится путем линеаризации в координатах левой части уравнения против условного времени контакта Пример. Газофазную необратимую реакцию пиролиза хлорпроизводного Пример. Газофазную необратимув о реакцию пиролиза хлорпроизводного
изучали в змеевиковом реакторе, близком к модели идеального вытеснения, прн r=const и общем давлении 0,1 МПа. Одиу серию опытов проводили без разбавителя, а другую — с разбавлением инертным газом в соотношении 1:1, Получены следующие результаты:
Найти кинетическое уравнение, константу скорости и ее доверительный интервал, используя линейный и нелинейный МНК, установить адекватность уравнения опыту, имея в виду, что спеднее отклонение в Ха в четырех па* раллельных опытах составило , а дисперсия воспроизводимости рав на Из литературных данных известно, что пиролиз хлорнроизводных обыч> «о протекает по реакции первого порядка. Проверяем эту гипотезу, обрабатывая опыты по уравнению 2 из табл. 10. где для первой серии опытов н для второй . Рассчитываем для каждого Найти кинетическое уравнение, константу скорости и ее доверительный интервал, используя линейный и нелинейный МНК, установить адекватность уравнения опыту, имея в виду, что спеднее отклонение в Ха в четырех па* раллельных опытах составило на Из литературных данных известно, что пиролиз хлорнроизводных обыч> «о протекает по реакции первого порядка. Проверяем эту гипотезу, обрабатывая опыты по уравнению 2 из табл. 10. где для первой серии опытов и откладываем ее против опыта функцию опыта функцию (рис. 18). Соответствие их прямой свидетельствует о вероятной адекватности упавнения зкг.певименту. Поиск константы ведем по уравнению , тем же способом, как в предыдущем примере. Находим значение . После этого аналогичным образом находим дисперсию адекватности, которая получилась равной 0,0100, Для оценки адекватности уравнения требуется найти среднее отклонение й функции
дисперсию адекватности, которая получилась равной 0,0100, Для оценки адекватности уравнения требуется найти среднее отклонение й функции
При средних значениях находим
что меньше табличного значения дисперсию константы, ее среднюю квадратичную* ошибку и доверительный интервал:
С учетом последнего устраняем лишние значащие цифры в константе скоро.* сти и получаем кинетическое уравнение:
L. применением нелинеииогоМНК поиск константы проводили на цифровой ЭВМ по mhhhmvmv
Обратимые реакции в интегральных условиях. Ранее быж> показано, что кинетические уравнения обратимых реакций при определенных условиях и известной константе равновесия могут иметь только одну неизвестную константу
где до достаточно высоких степеней конверсий, по иц'геГральйЫй формам уравнений (II-70) и (II-71). В последнем из них, как й раньше, распространенных способов решения состоит в преобразовании кинетического уравнения как функции «движущих сил»обрати-- мой реакции, т. е. равновесные концентрации, степени конверсии или полнота реакций Подобно этому для обратимых реакций, имеющих первый и второй или вторые порядки в обоих направлениях, получают такие выражения скорости:
С другой стороны, из выражения для константы равновесия
вый порядок в обоих направлениях, получим: где из-выражения для константы равновесия соответственно через Решения некоторых интегралов для периодических условий и реакций, в которых порядки совпадают со стехиометрически- ми коэффициентами, приведены в табл. 11. Аналогичные уравнения можно вывести и для газофазных реакций в условиях идеального вытеснения. Для реакций 1, 5, б и 8 они будут совпадать с приведенными в табл. 11 решениями, но с заменой концентраций на парциальные давления, а времени t — на Если представлять экспериментальные данные в координатах уравнений из табл. II, при правильности исходной гипотезы получим прямые, по которым предварительно проверяем адекватность уравнения опыту. Обработка эксперимента, как и раньше, проводится линейным или нелинейным МНК с нахождением приведенных выше констант или их комбинаций. Из них, зная константу равновесия, легко рассчитать Обосновать механизм, кинетическое уравнение, определить константы прямой и обратной реакции, а также их доверительные интервалы, если нри четырех паоаллельных опытах среднее отклонение измерений составляло
Для такого кинетического уравнения обработку опытов ведем по формуле 5 из табл. 11. Из выражения для константы равновесия находим
Далее рассчитываем для каждой точки левую часть формулы 5 и откладываем нолученные данные против времени (рис. 19), что указывает на вероятную адекватность уравнения экснерименту. Путем линейного МНК по уравнению сию воспроизводимости в функции у находим по среднему отклонению в параллельных опытах: 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
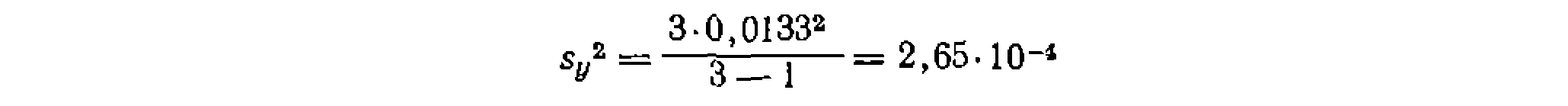
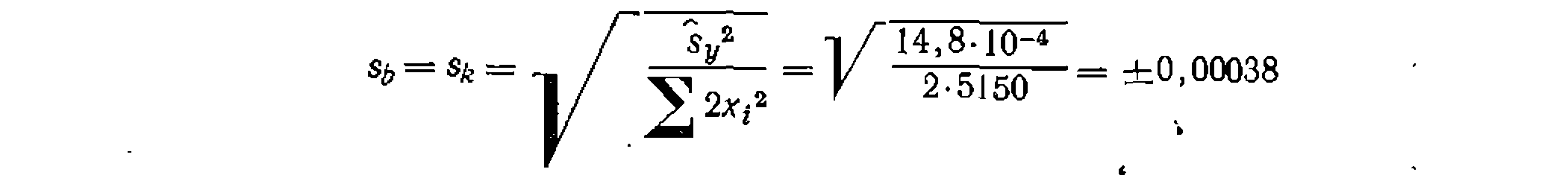
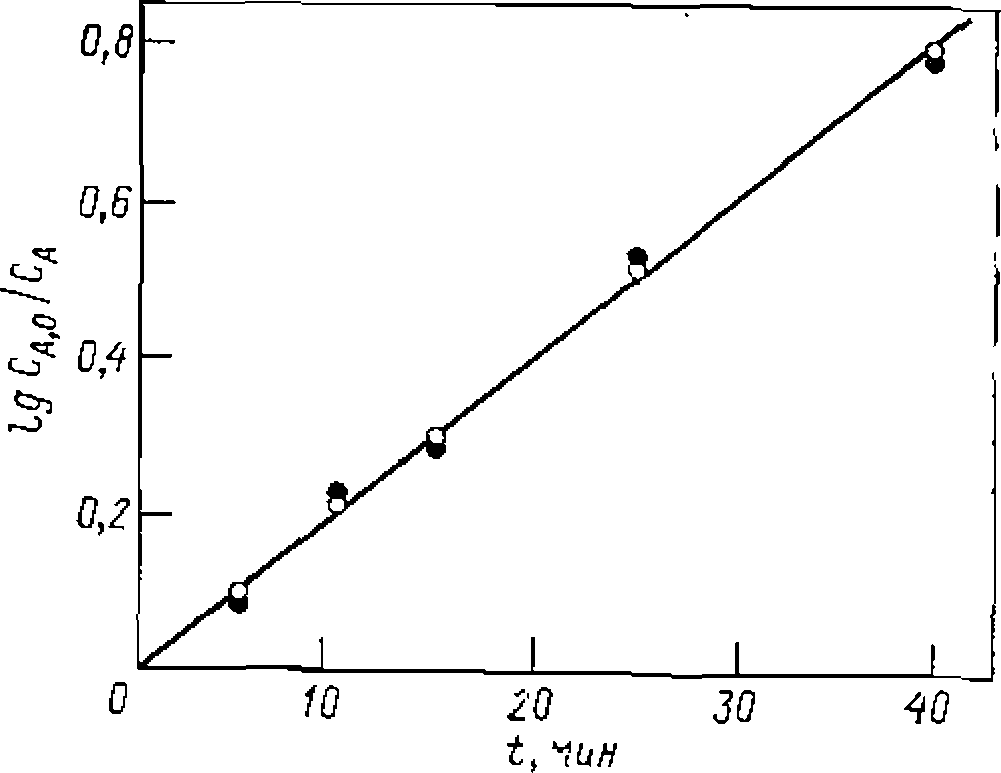
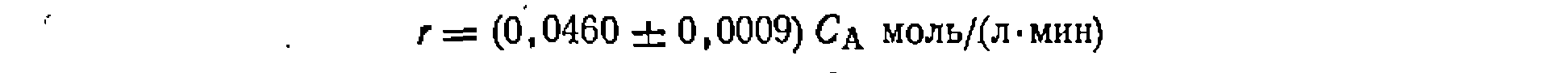
 и предварительно убеждаемся в вероятности принятой гипотезы. После этого по тангенсу угла наклона прямой на рис. 17 приблизительно оцениваем величину константы скорости. Положим, что оиа получилась равной 0,046. Преобразуем интегральный вид уравнения в форму, разрешенную относительно
и предварительно убеждаемся в вероятности принятой гипотезы. После этого по тангенсу угла наклона прямой на рис. 17 приблизительно оцениваем величину константы скорости. Положим, что оиа получилась равной 0,046. Преобразуем интегральный вид уравнения в форму, разрешенную относительно  , и рассчитываем нацифровой ЭВМ для каждой экспериментальной точки значения
, и рассчитываем нацифровой ЭВМ для каждой экспериментальной точки значения  н
н 

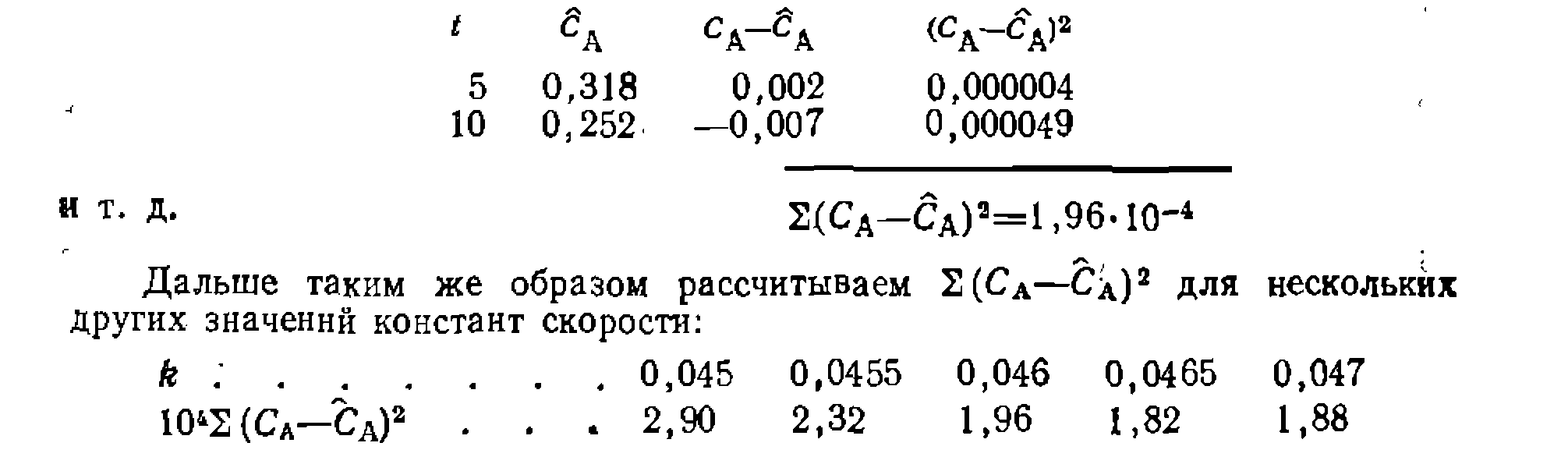
 , составляя 1,8-10-4, Дисперсия адекватности
, составляя 1,8-10-4, Дисперсия адекватности 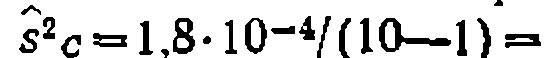
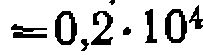 .что дает критерий Фишера, равный
.что дает критерий Фишера, равный 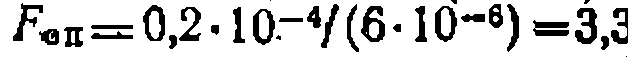 I,
I, . Дисперсия константы для уравнения с одним неизвестным па
. Дисперсия константы для уравнения с одним неизвестным па . В данном, случае получим
. В данном, случае получим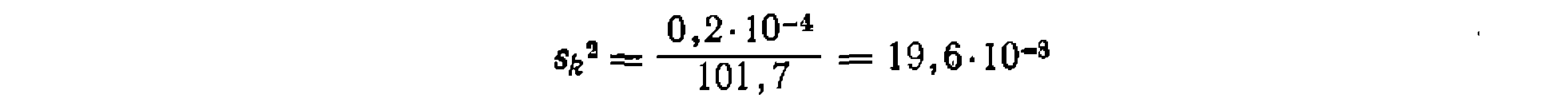
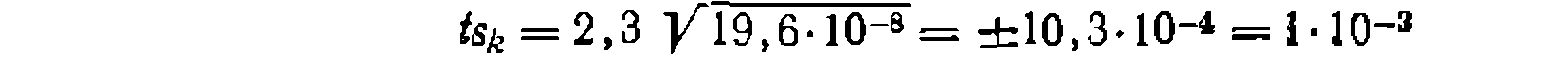
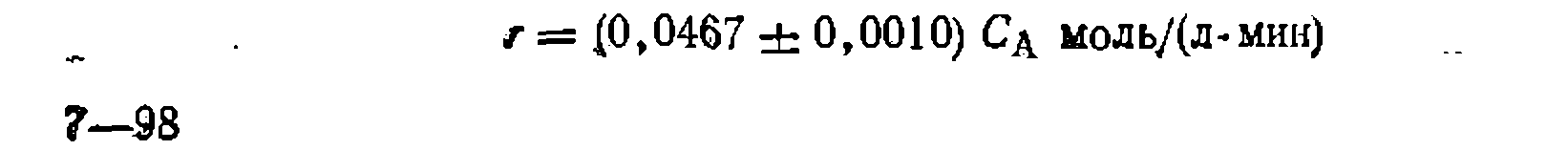
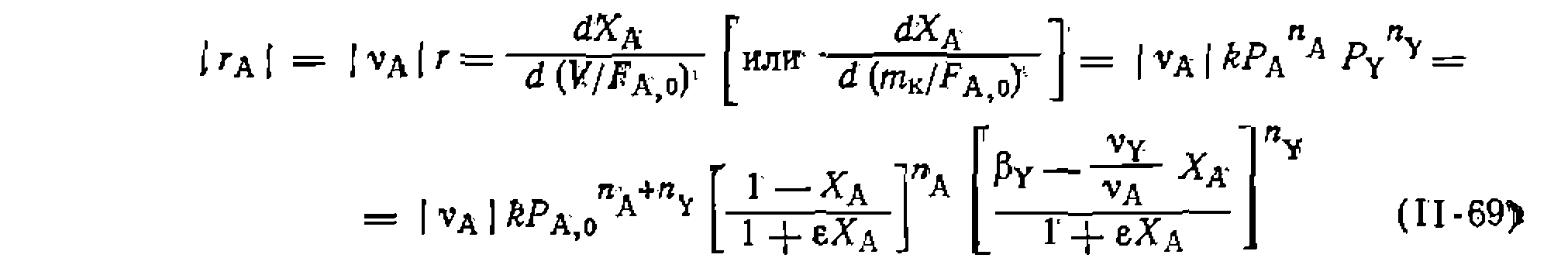
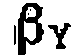 — мольное (объемное) соотношение- реагентов Y и А в исходной емеси.
— мольное (объемное) соотношение- реагентов Y и А в исходной емеси.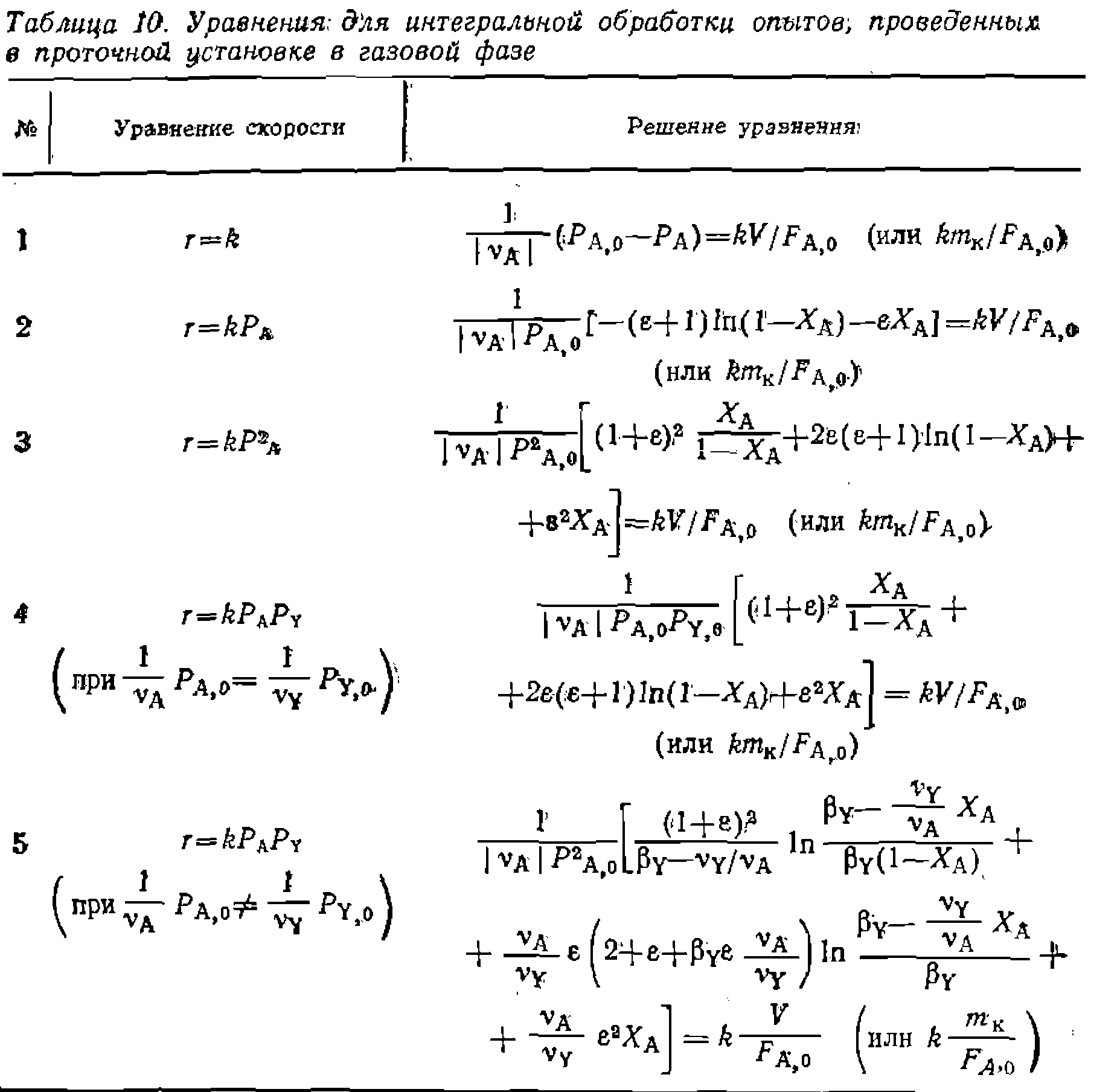
 ,
,  и в других частных случаях. Некоторые из наиболее распространенных примеров решений приведены в табл. 10.
и в других частных случаях. Некоторые из наиболее распространенных примеров решений приведены в табл. 10.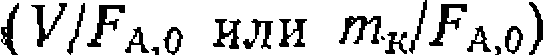 . Поиск константы по нелинейному МНК проводят по минимуму суммы квадратов отклонений в степени конверсии
. Поиск константы по нелинейному МНК проводят по минимуму суммы квадратов отклонений в степени конверсии 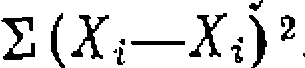
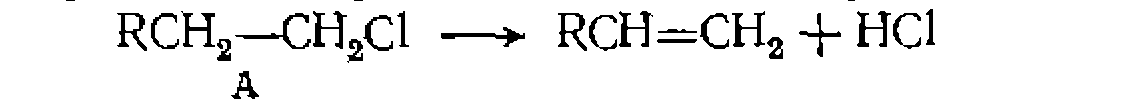

 , а дисперсия воспроизводимости рав
, а дисперсия воспроизводимости рав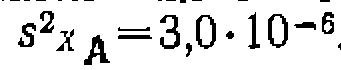
 и для второй
и для второй  . Рассчитываем для каждого
. Рассчитываем для каждого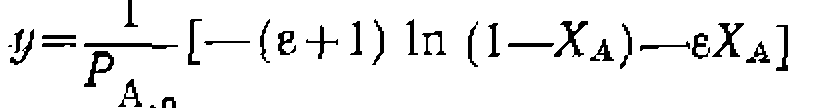 и откладываем ее против
и откладываем ее против (рис. 18). Соответствие их прямой свидетельствует о вероятной адекватности упавнения зкг.певименту. Поиск константы ведем по уравнению
(рис. 18). Соответствие их прямой свидетельствует о вероятной адекватности упавнения зкг.певименту. Поиск константы ведем по уравнению , тем же способом, как в предыдущем примере. Находим значение
, тем же способом, как в предыдущем примере. Находим значение  . После этого аналогичным образом находим
. После этого аналогичным образом находим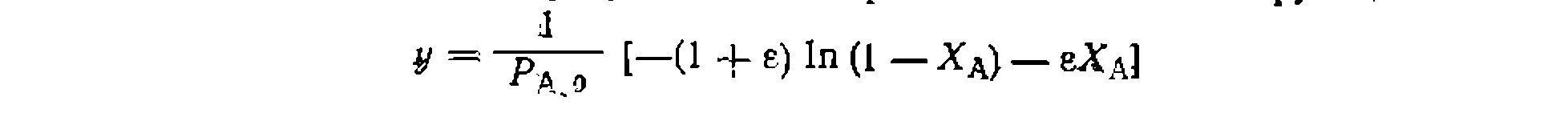
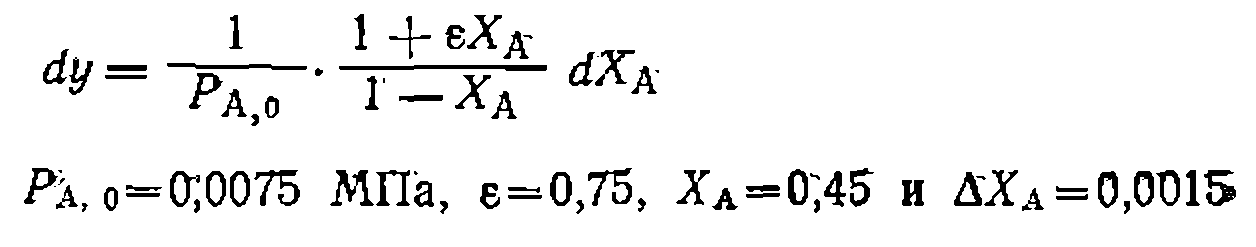
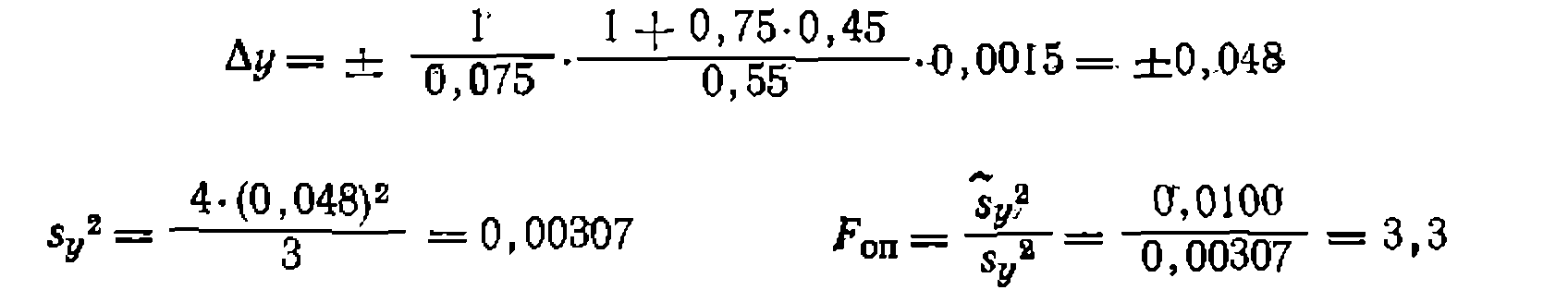
 . Прежним- способом находим
. Прежним- способом находим
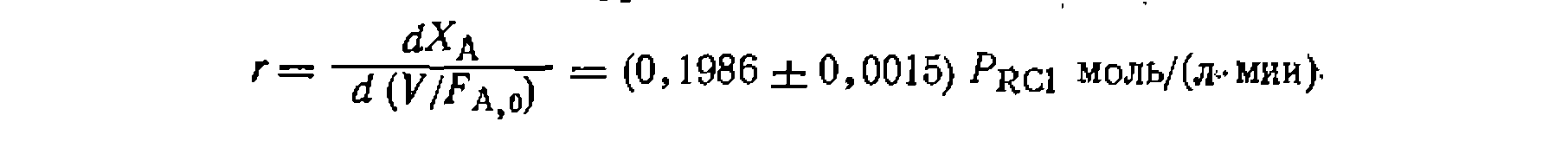
 . В -пез^ьтате пол\чаем: /£=0.19887..
. В -пез^ьтате пол\чаем: /£=0.19887..
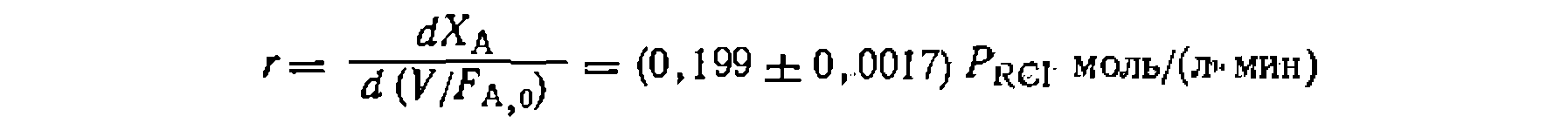
 (элементарную или эффективную), причем из-з?а термодинамического соответствия кинетики прямой и обратной реакций эти кинетические уравнения имеют следующий вид:
(элементарную или эффективную), причем из-з?а термодинамического соответствия кинетики прямой и обратной реакций эти кинетические уравнения имеют следующий вид: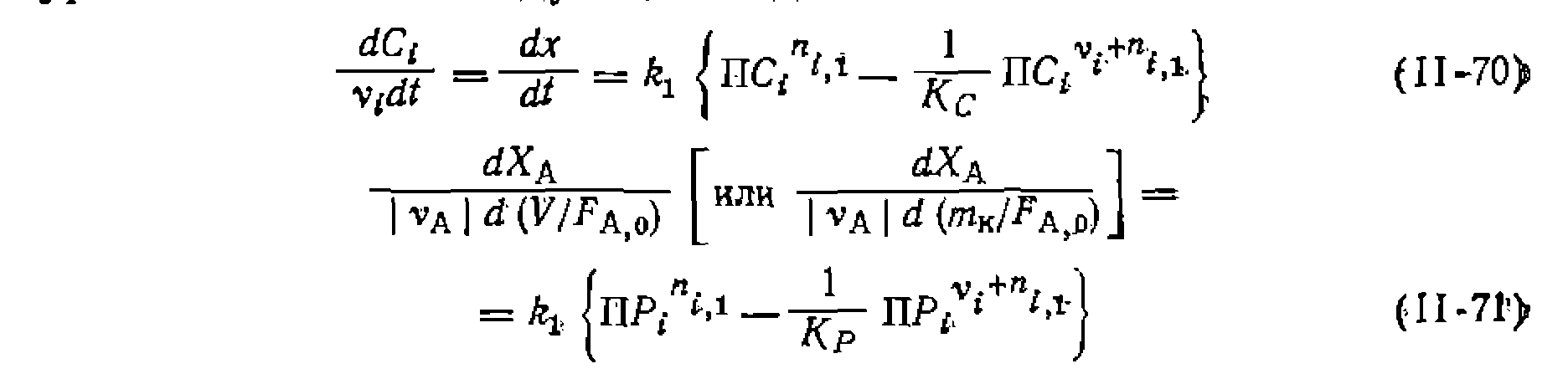
 —порядки прямой реакции,., а
—порядки прямой реакции,., а  —стехи о метрические коэффициенты с соответствующим знаком.. Поэтому кинетику обратимых реакций нередко изучают методом изолирования» т. е. по начальным скоростям илн в* условиях,, далеких от равновесия, когда можно пренебречь скоростью обратной реакции. Определив из проведенных опытов
—стехи о метрические коэффициенты с соответствующим знаком.. Поэтому кинетику обратимых реакций нередко изучают методом изолирования» т. е. по начальным скоростям илн в* условиях,, далеких от равновесия, когда можно пренебречь скоростью обратной реакции. Определив из проведенных опытов  и
и  и зная Кт легко лучить общее кинетическое уравнение реакции. Более общее н достоверное решение состоит в обработке опытов., проведенных
и зная Кт легко лучить общее кинетическое уравнение реакции. Более общее н достоверное решение состоит в обработке опытов., проведенных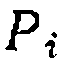 обычно заменяют через
обычно заменяют через  . Один из
. Один из или
или  , где
, где  —
— Так, для реакции А^В, имеющей пер
Так, для реакции А^В, имеющей пер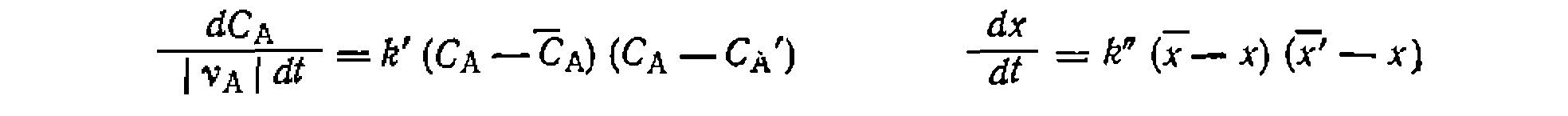
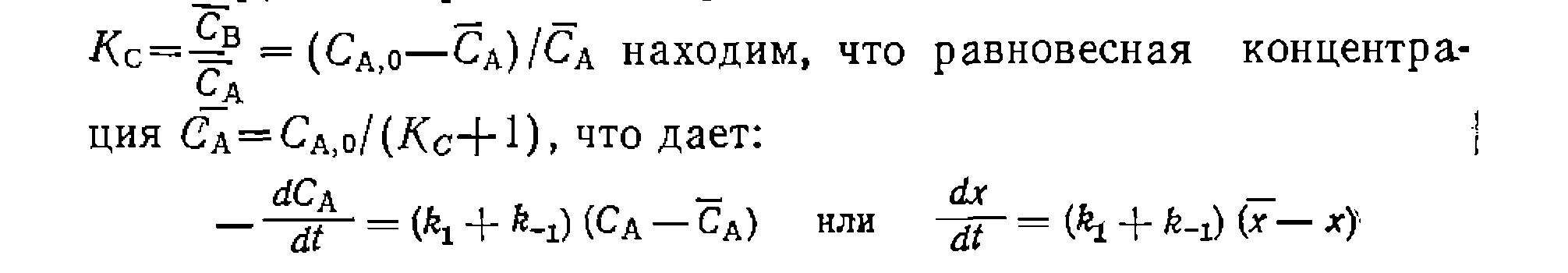
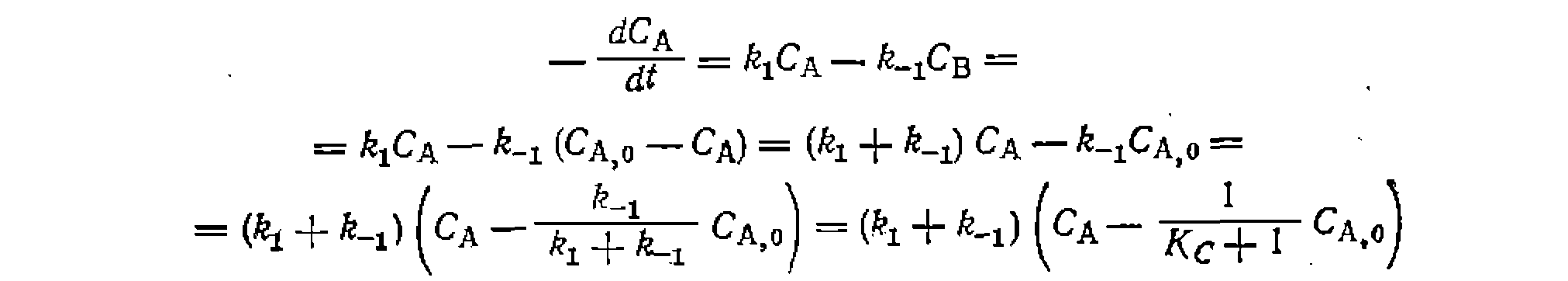
 —корни квадратного уравнения, получаемого
—корни квадратного уравнения, получаемого — константа или некоторая функция констант прямой и обратной реакций.
— константа или некоторая функция констант прямой и обратной реакций. или
или  .В других случаях необходимо учитывать изменение объема во время реакции.
.В других случаях необходимо учитывать изменение объема во время реакции. и
и 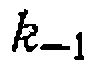
 и дисперсия воспроизводимости была равна
и дисперсия воспроизводимости была равна  Из литературы известно, что для реакций этерификации и гидролиза сложных эфиров наиболее распространен механизм, согласно которому кинетическое уравнение имеет второй порядок в обоих направлениях, т. е.
Из литературы известно, что для реакций этерификации и гидролиза сложных эфиров наиболее распространен механизм, согласно которому кинетическое уравнение имеет второй порядок в обоих направлениях, т. е.

 , где
, где  и
и 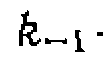 — эффективные константы, включающие концентрацию катализатора.
— эффективные константы, включающие концентрацию катализатора. и
и 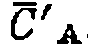
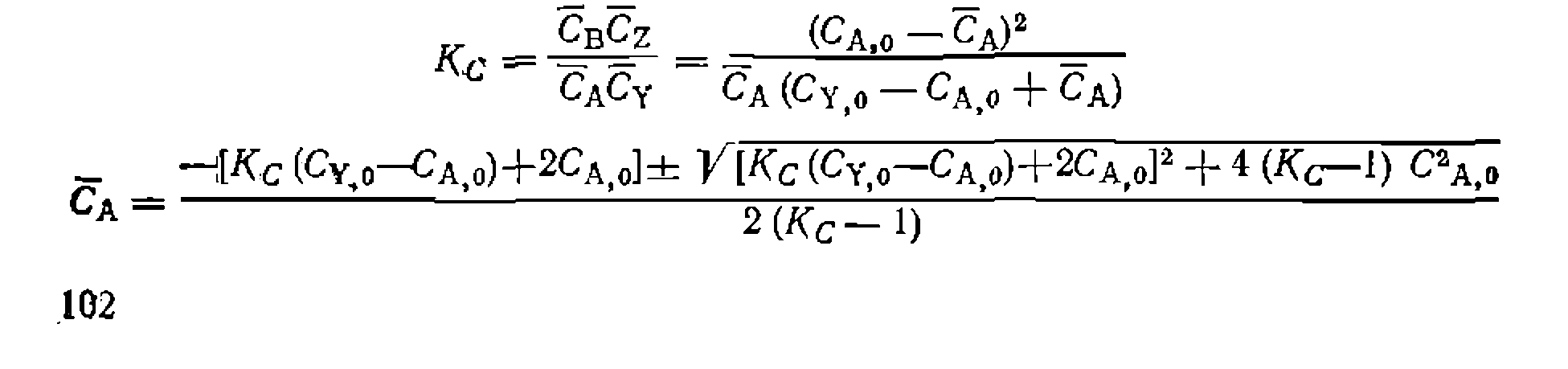
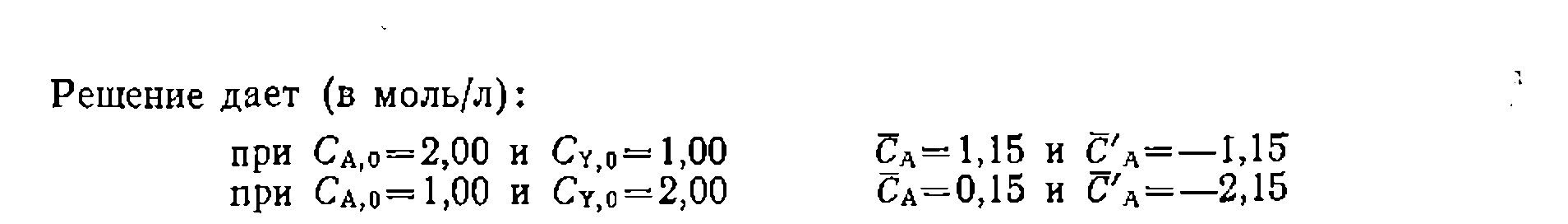
 иаходим
иаходим  л/(моль-мин) и
л/(моль-мин) и 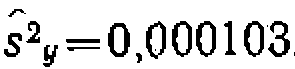 . Диспер
. Диспер . Для этого дифференцируем функцию у
. Для этого дифференцируем функцию у