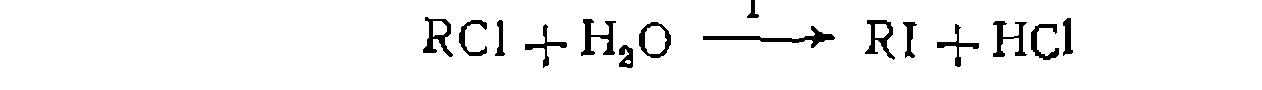|
|
Кинетическая модель будет состоять из трех дифференциальных уравпеннй скорости для ключевых веществ
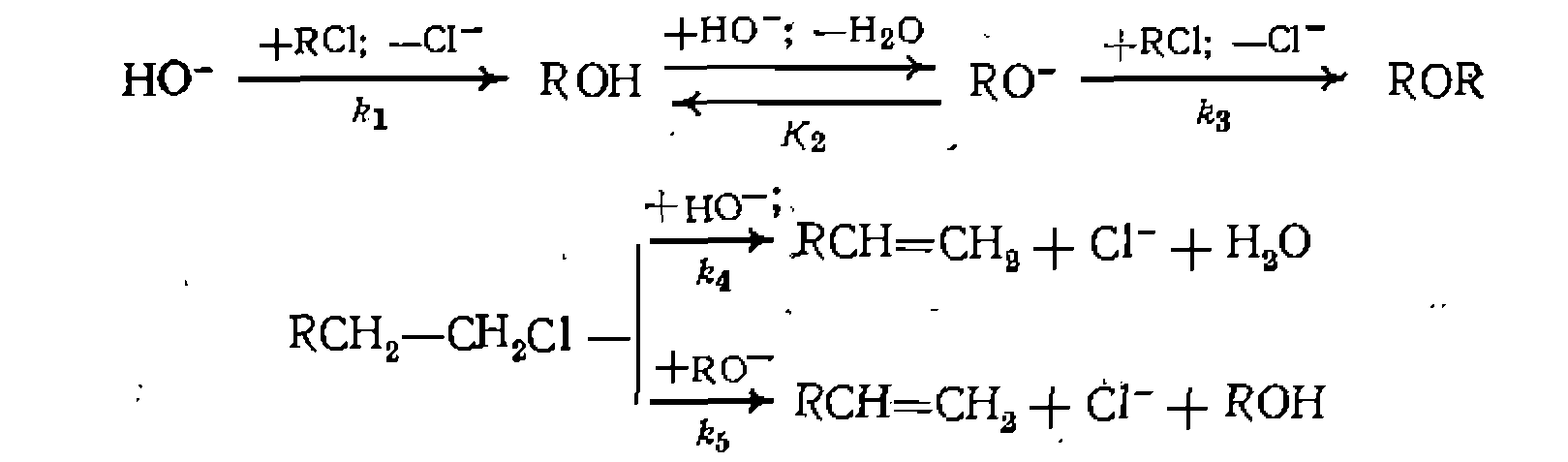
ния имеем такую схему превращений, учитывающую существование основания в двух формах (НО~ и RO~):
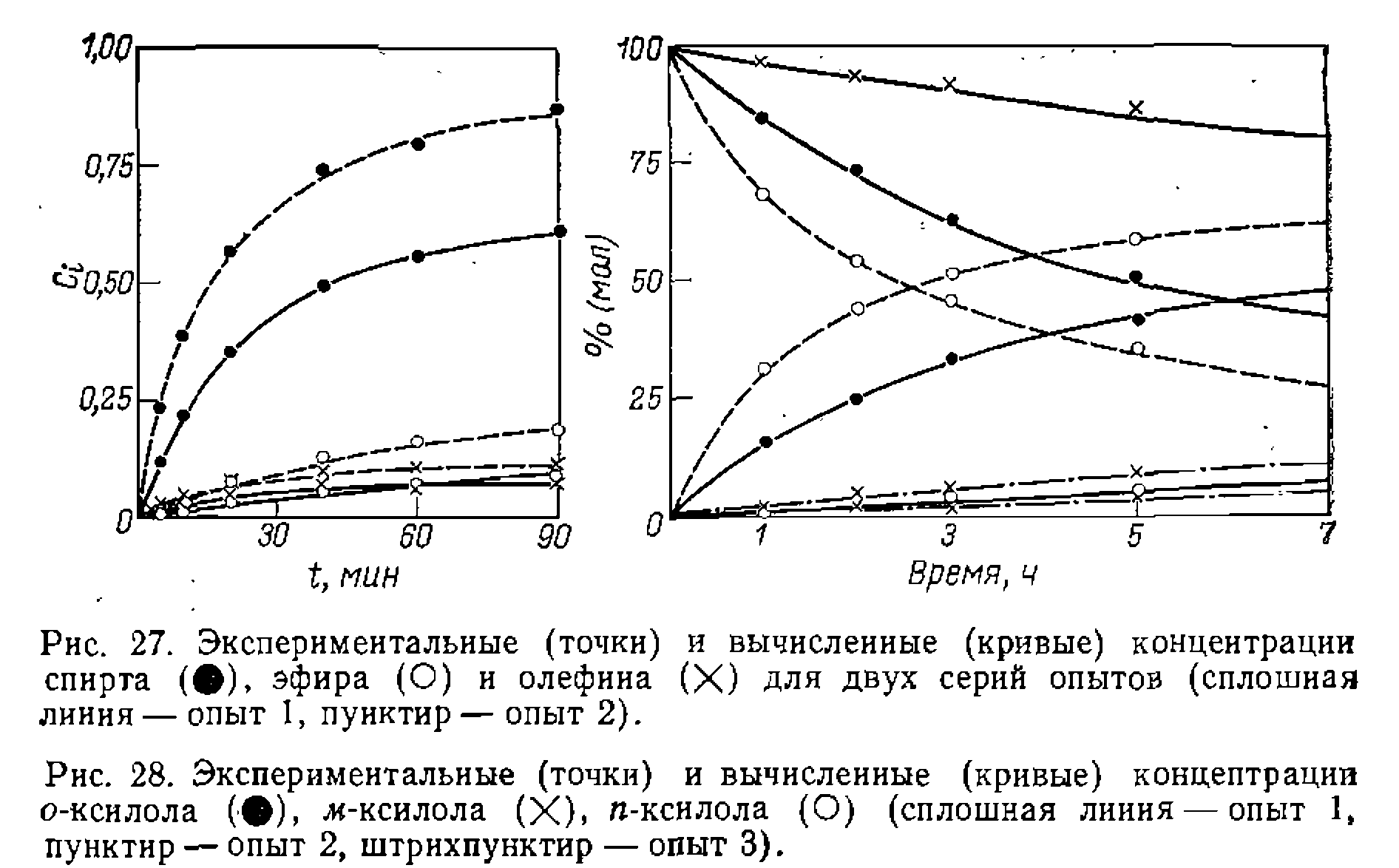
Опытные и вычисленные данные сопоставлены на рис. 2^7.
В результате получаем: По этим уравнениям поиск констант проводим на ЭВМ по минимуму взвешенной суммы квадратов отклонений в концентрациях спирта, эфира н олефина, т. е. Так как
Известно, что реакции изомеризации мономолекулярны, и система описывается следующими дифференциальными уравнениями:
В уравнениях содержится пять неизвестных, так как одна коистапта равновесия равна произведению двух других (для дальнейших вычислений исключим константу всех коистант таким образом, чтобы достигалея минимум остаточной суммы квадратов по концентрациям всех веществ. В результате получаем: При проведении этого процесса в присутствии хлорида алюминия как катализатора в растворе толуола в периодических условиях получены такие результаты при общей концентрации ксилолов 0,800 моль/л:
Пример 2. Известно, что изомеризация ксилолов обратима, нричем возможна следующая схема превращений:
Естественно, что при таком расчете можно было бы не подходить к системе как к полностью неизвестной, а учесть имеющиеся в литературе дай-
ные по равновесию и результаты предварнтельпого анализа экспсримепта* показывающие, что при t—>-0 скорости образования пара-изомера из о-кси- лола, а носледнего— из ДИФФЕРЕНЦИАЛЬНЫЙ МЕТОД ОБРАБОТКИ КИНЕТИЧЕСКИХ ДАННЫХ ДЛЯ СЛОЖНЫХ РЕАКЦИЙ Этот метод уже рассматривался в приложении к простым и обратимым реакциям, а для сложных систем он имеет особенные преимущества. Они состоят не только в значительном упрощении уравнений, по которым обрабатывают кинетические данные, но и в более простом анализе схемы превращений и состава образующихся продуктов, определении соотношений отдельных констант. Кроме того, нередко появляется возможность обработки данных для каждой из исследу|^шх реакций в отдельности. По этим причинам сложные системы реакций, даже изучаемые в интегральных условиях, нередко обрабатывают дифференциальным методом, находя их скорости дифференцированием кинетических кривых. Соотношение констант скорости,для параллельных реакций находят из выражения, полученного делением кинетических уравнений с сокращением временных характеристик процесса:
При этом разности порядков реакциивытекают из гипо тезы о механизме реакций.
Для последовательных реакций первого порядка и для последовательно-параллельных превращений
имеем одинаковое уравнение-
по которому легко найти Наконец, при установлении неизвестной схемы превращений, что рассматривали раньше на примере дегидрирования этилбензола, можно подтвердить пути образования бензола и толуола линеаризацией более простых уравнений:
Возможность обработки кинетических данных для любой из исследуемых реакций в отдельности появляется для систем, в которых каждое из ключевых веществ образуется только по одной простой или обратимой реакции, например:
Здесь для скорости образования каждого из трех конечных продуктов С, D и Е можно записать уравнения
а скорость первой реакции выразить так:
При этом скорости превращения веществ ляют для каждой экспериментальной точки по соответствую-
а скорости реакций видно, что в таком варианте обработка данных сводится к ранее рассмотренной задаче поиска констант для простых н обратимых реакций.
были получены следующие результаты:
Требуется найти константы скорости, проверить адекватность модели и определить доверительные интервалы констант, если в четырех параллельных опытах среднее отклонение Для скорости второй реакции можно заннсать выражение
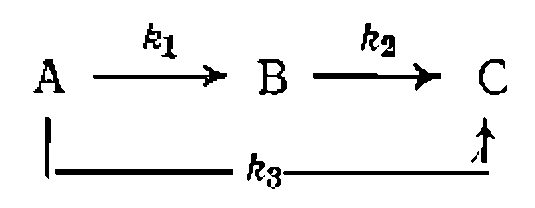
Пример. При изучении в проточно-циркуляционной установке системы газофазных реакций предполагаемого нервого порядка из которого следует, что помощью линейного МНК поуравнению
которое преобразуем в линейную форму:
Для первой (обратимой) реакции записываем уравнение
что соответствует
Среднее отклонение в функции у равно
Для других сложных реакций, включающих два или более пути образования продуктов, изложенный способ обработки данных не годится. Тогда поиск констант ведут по системам кинетических уравнений, добиваясь минимизации взвешенной суммы квадратов отклонений (или при равенстве дисперсий воспроизводимости— простой суммы квадратов отклонений) для всех ключевых веществ. Пример. При изучении в периодических условиях системы реакций, имеющих предноложительно первые порядки В результате получаем:
кнпетические кривые были продифференцированы в ряде точек, что дало такие результаты (время в мин): /. J.
с .Требуется найти констапты скорости, их доверительные интервалы и проверить адекватность уравнений опыту, если концентрации Св и Сс имели в четырех параллельных опытах одинаковое среднее отклонение ±0,002 моль/л, а скорости находили с ошибкой ±5%. Критерий Фишера
мнпнмизнруя суммы квадратов отклонений в концентрациях В и С, по которым проводили анализ реакционпых смесей. В результате расчета на ЭВМ получаем (в мип-1):
Для поиска констапт используем два уравнения скорости ИССЛЕДОВАНИЕ ВЛИЯНИЯ ТЕМПЕРАТУРЫ Влияние температуры на состав продуктов, селективность и скорость реакций проявляется через зависимость От нее параметров реакций, т. е. констант скоростей, равновесия, адсорбционных коэффициентов, коэффициентов диффузии и др.:
Здесь
Для полной характеристики процесса при его исследовании необходимо найти лредэкспоненты, энергию активации или энтальпии всех параметров, входящих в кинетическую модель. Классический и наиболее распространенный способ состоит в том, что вначале описанными выше методами при некой температуре находят концентрационные зависимости скорости реакций, кинетическую модель процесса и ее константы. Считая, что модель сохраняет свой вид н при других температурах, проводят опыты при 2—4 других температурах, определяя соответствующие параметры. Число дополнительных опытов можно сократить по сравнению с первоначальной серией, но оно должно быть достаточным для нахождения всех констант. Это означает, что при наличии в уравнении только одной константы можно даже не изменять условия дополнительных опытов, но при увеличении числа неизвестных параметров такое варьирование необходимо, хотя и в ограниченных пределах, определяемом типом модели. После нахождения констант при нескольких температурах находят активационные параметры или энтальпию процесса по линеаризованной форме, приведенных выше уравнений типа уравнения Аррениуса:
В координатах висимость с тангенсомугла наклона, равным
помощи линейного МНК по минимуму суммы квадратов отклонений в найденных и рассчитанных значениях
отклонений мых величин находят обычным образом, устраняя в них лишние значащие цифры. Из предэкспоненциального множителя в уравнении Аррениуса можно затем найти энтропию активации.
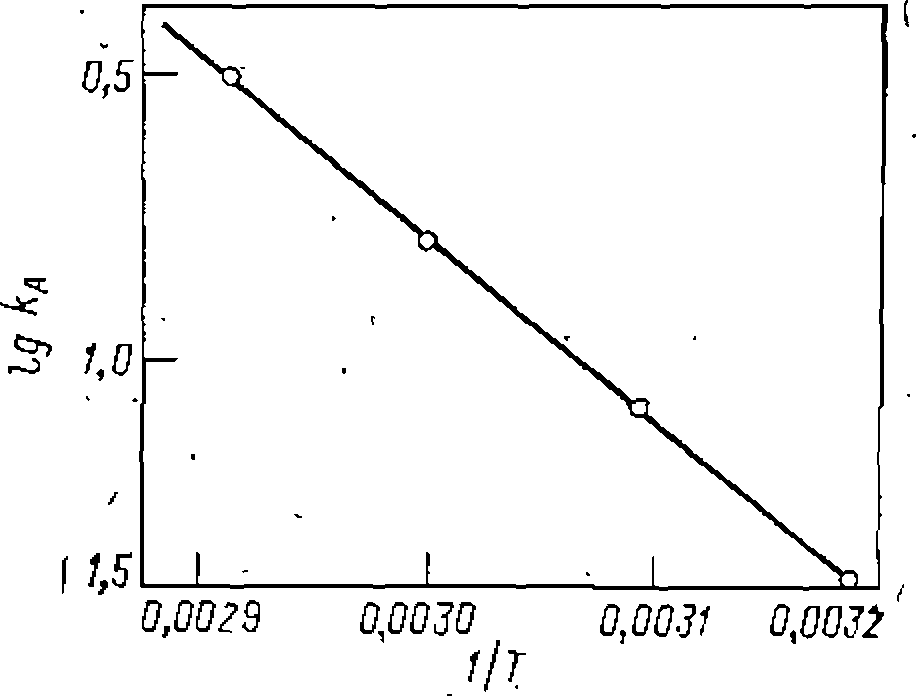
Рис. 29. Линеаризация уравнения Арреннуеа,- в первой серии опытов прн323 К были найдены уравнение скорости ведены опыты еще прн трех темнературах и при давшие следующие результаты:
Из этих опытов путем линейного МНК по уравнению
Исходя нз значения предэкспоненциального множителя рассчитываем энтропию активации:
После расчета доверительных интервалов окончательно имеем: Она получилась отрицательной, как и следовало ожидать для элементарной реакции Е2-отщепления. Кроме рассмотренного способа все чаще применяют другой, при котором параметры для- каждой температуры специально не рассчитывают, а в кинетическое уравнение или модель заранее включают температурную зависимость этих параметров:
При этом для нахождения активационных параметров используют весь массив экспериментальных данных, что снижает ошибки и степень закоррелированности констант. Отметим, что для газофазных реакций активационные параметры правильнее находить по уравнениям, выраженным через концентрации, а не через парциальные давления. Это объясняется тем, что закон действия масс относится к концентрациям веществ, которые при постоянном действии зависят от температуры в соответствии с уравнением Пример. Реакцию термического хлорирования в газовой фазе изучали в проточно-циркуляционной установке при большом избытке углеводорода и общем давлепии 0,1 МПа. Получены следующие результаты: Показатели При! 683 К При 603 К При 623 К
Требуется определить кнпетическое уравнение, активащюшш.е параметры и их доверительные интервалы, еслн среднее отклонение значенийпри трех параллельных опытах составило ±0,03. Для реакций термического хлорирования в газовой фазе ранее был найден оял кинетических уравнений, нз которых наиболее вероятное
Вопросы и упражнения
При помощи линейного МНК находим:
И легко преобразуется в линеаризованную форму путем логарифмирования:
1.Суммируйте все преимущества и недостатки линейного и нелинейного МНК при обработке результатов опытов. 2.Перечислите все признаки неадекватности кинетических уравнений или моделей эксперименту. 3.При изучении некоторой реакции при четырех параллельных опытах были найдены такие значения Са: 0,363, 0,359, 0,362 и 0,364. Прн обработке опытов с помощью нелнпейного МНК получены следующие опытные и рассчитанные значепия концелтрацйй:
Определите адекватность уравнения опыту, если 1. 4.Обоатнмая реакция A+Y^±B описывается кинетическим уравнением
найдите решение этого уравнения, по которому будет проводиться интегральная обработка данных в периодических условиях. * 5.Реакции А—>-В соответствует кинетическое уравнение
получены в периодиче-
б. При параллельных реакциях гких условиях такие количества продуктов:
Покажнте, что реакции имеют одинаковые порядки, н определите соотношение копстант скорости и его доверительный интервал.
а также выведите урав 7.Выведите интегральное уравнение для расчета соотношения констант скорости параллельных реакций нения для выхода н селективности по продукту В. 8.Для последовательных реакций первого порядка А—»-В—>-С найдите общее решение для максимума выхода (мольной доли) первого промежуточного нродукта в периодических условиях. Проанализируйте полученное решение с точки зрения влияния соотношения k^k\ на максимум выхода этого
одуктов: 9. При последовательно-параллельной реакции ских условиях получены следующие составы прод в периодиче-
нродукта. Постройте графики зависимостей и найдите соотношение 10. Прн газофазном превращ по суммарным реакциям А—»-В, са в проточио-циркуляциоиной у<
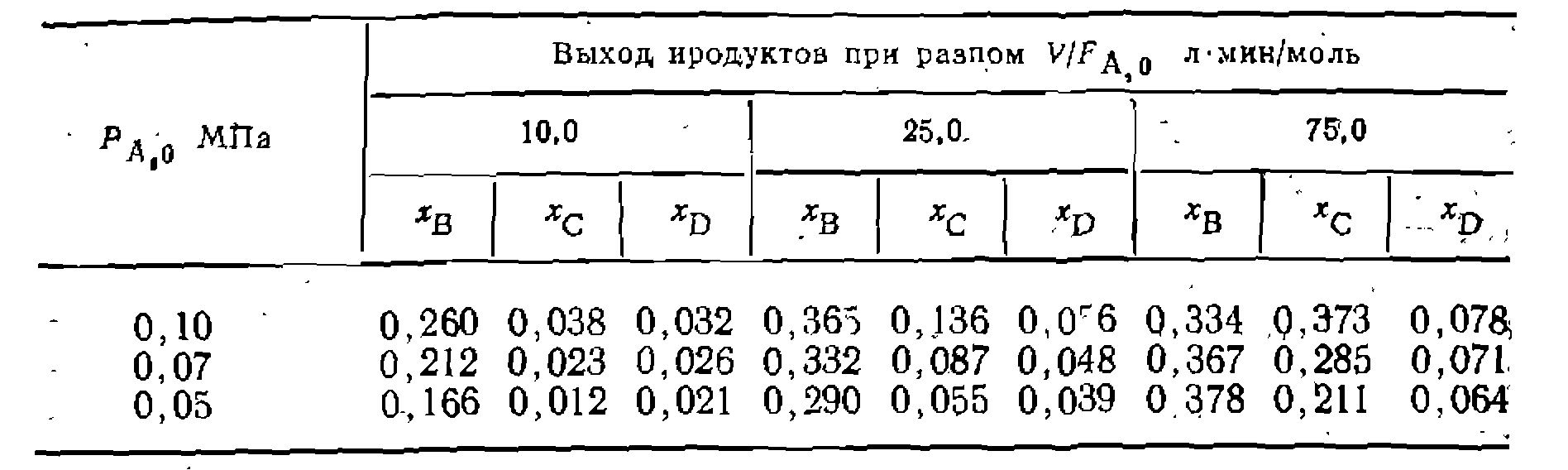
1еиии реагента А образуются три продукта А—и А—»-D. При исследовании процес-' становке были получены такие результаты:
Определите схему превращений, 'найдите соотношения констаит скорости, константы скорости и их доверительные интервалы, если дисперсия врспроизво- дпмости прн четырех- параллельных онытах была одинаковой, для асех продуктов неравной 0,00001. ■ - М. Выведите для безградиентных условий реакции зависимость выхода (мольной доли) первого промежуточного нродукта последовательных реакций первого порядка по каждому из реагентов как фупкцию
Сравните полученное решение с выведенным ранее для интегральных условий реакции. Найдите максимум выхода продукта В и сравните с ответом решения в примере 8. ГЛАВА III ГОМОГЕННО-КАТАЛИТИЧЕСКИЕ РЕАКЦИИ Гомогенно-каталитическими обычно являются жидкофазные реакции, протекающие в присутствии гомогенных катализаторов. При этом реагенты и катализатор могут находиться полностью в растворе или же поступать в него из другой (газовой или жидкой) фазы. Существуют три основных типа гомогенных катализаторов: 1) нуклеофильные; 2) кислотно-основные и электрофильные; 3) металлокомплексные. Принцип действия любого типа катализатора состоит в образовании активного промежуточного комплекса, который превращается в продукты, а катализатор при этом регенерируется:
Такой путь реакции ведет к ее ускорению благодаря снижению энергетического барьера по сравнению с некаталитическим процессом (рис. 30). В других случаях катализаторы способны вызывать реакции, вообще не протекающие в их отсутствие. Эффективность катализаторов часто характеризуют так называемым числом оборотов (turn-over number) катализатора, равным числу молекул реагентов, превращенных одной молекулой катализатора в секунду. Для нуклеофильных катализаторов это число при 25 °С составляет 10“7—10~2 моль*моль-1 *с-\ для металлокомплексных—1—104 моль-моль-1 «с^1, а для ферментов— 102—105 моль*моль"1*с~1. При большой эффективности во многих процессах гомогенному катализу присущи и недостатки, из которых общими являются необходимость отделения (отмывки) катализатора от реакционной смеси, образование токсичных сточных вод и повышенный расход катализатора на единицу количества продукта. В некоторых случаях гомогенные катализаторы вызывают коррозию материалов; кроме того, учитывая их высокую стоимость, необходимо проводить регенерацию катализатора, что усложня- Рис. 30. Энергетические профили некаталитической (1) и гомогениоката- лнтической (2) реакций. ет производство. В связи с этим намечается тенденция за- ^ мены, где это возможно, гомо- ^ генных катализаторов на гете- £ рогенные, а также их фиксации (иммобилизации) на твердых поверхностях или на полимерах. Тем не менее гомогенный катализ продолжает играть важную роль в технологии органического синтеза, особенно при жидкофазном хлорировании, этерификации, алки- лировании, окислении, оксосинтезе, конденсации карбонильных соединений и при других многотоннажных процессах. При возможности выбора гомогенных катализаторов руководствуются рядом требований, среди которых отметим достаточно высокие активность и селективность, доступность и относительно низкую стоимость, пониженные коррозионную активность и воздействие на окружающую среду и т. д. НУКЛЕОФИЛЬНЫЙ КАТАЛИЗ И ЕГО МЕХАНИЗМ Наиболее распространенными нуклеофильными катализаторами являются ионы галогенов
Но конечному результату нуклеофильные каталитические реакции можно подразделить на реакции присоединения и замещения. В реакциях нуклеофильного присоединения YH по кратным связям
По такой схеме происходит нуклеофильное присоединение по карбонильной груцде реагента с кислотными свойствами, на-
Образующийся промежуточный анион регенерирует затем катализатор по протолитической реакции с YH: роль нуклеофильного катализатора часто выполняет анион Y-— сопряженное основание реагента, который обладает значительно более сильными нуклеофильными свойствами, чем YH, и легко присоединяется по кратной связи: стример синильной кислоты:
гут быть Наприме
Парой оеагент (YH)—катализатор (Y~) в этих реакциях мо- а на следующей стадии происходит присоединение нуклеофильного катализатора Y- с одновременной его регенерацией из мо лекулы YH:
В других случаях реакция может идти сразу по обоим механизмам. Нуклеофильный катализ эффективен в аналогичных реакциях присоединения YH к олефинам с электроиоакцепторным заместителем при кратной связи
При этом нередко за счет водородной связи вначале образуются промежуточные комплексы между реагентами, что снижает электронную плотность на реакционном центре и ускоряет реакцию. Например, так протекают реакции с аналогами карбонильных соединений — нитрилами: Нуклеофильный катализ сопряженными основаниями характерен также для реакций присоединения YH к гетероциклическим соединениям с малыми циклами. Как н в реакциях присоединения по кратным связям, исходный реагент активируется за Широко распространен нуклеофильный катализ в реакциях замещения по карбоксильной группе производных карбоновых кислот. Для превращений ангидридов и хлор ангидридов активными нуклеофильными катализаторами являются третичные амины. Механизм этих реакций заключается в промежуточном образовании катиона ацилпиридиния (или ациламмония В реакциях замещения, протекающих при насыщенном атоме углерода, свойствами активного нуклеофила и одновременно легко замещаемой группы обладают анионы иода и брома. Примером могут служить реакции гидролиза хлор- или бромпроиз- водных при катализе анионом иода:
Замещение RZ+Y—^RY+Z при нуклеофильном катализе в простейшем случае представляет собой чередование двух реакций нуклеофильного замещения:
Катализ сопряженными основаниями наиболее эффективен для реакций присоединения спиртов, карбоновых кислот, фенолов, меркаптанов, сероводорода и синильной кислоты к а-оксидам:
Образовавшийся комплекс взаимодействует затем с катализатором У~ и присоединяет протон от YH с одновременной регенерацией Y-:
счет образования водородной связи с YH:
вертичного азота и отсутствию сопряжения с С=О-группой:
В реакциях алкоголиза сложных эфиров возможен нуклеофильный катализ другого типа, в котором в качестве катализатора используется сопряженное основание реагента. Так же как в реакциях присоединения, повышенная нуклеофильность сопряженного основания по сравнению с реагентом позволяет резко .ускорить-процесс (сравнительно с некаталитическим):
КИНЕТИКА РЕАКЦИЙ НУКЛЕОФИЛЬНОГО КАТАЛИЗА
При другом механизме нуклеофильного катализа промежуточный комплекс Практически все рассмотренные в предыдущем разделе реакции можно представить двумя общими схемами. Одна из них включает образование комплекса между реагентами (за счет водородной связи), его реакцию с нуклеофильным катализатором Схема упрощается, если первая стадия является реакцией присоединения (отсутствует Z), а вторая стадия мономолекуляриа (отсутствует Y). Кроме того, первая стадия может быть необратимой Схема (Ш-2) характерна не только для нуклеофиль- цого катализа. По этой причине приведенный ниже кинетический анализ й методология кинетического исследования имеют ^бщий характер :для.всех гомогенно-каталитических реакций. Для кинетического анализа схемы (Ш-2) выведем уравнение скорости реакции для наиболее общего случая, когда пер* вая стадия обратимая реакция замещения, а вторая стадия бимолекулярна. Примем, что концентрация катализатора мала по сравнению с концентрацией реагентов и последние не обра- зуют друг с другом каких-либо комплексов. Применяя метод: стационарных концентраций к промежуточному каталитическое му комплексу, получим: Отсюда
и скорость реакции равна
Последнее уравнение аналогично выражению (II-37), выведенному в главе II для некаталнтической реакции. Оно требует, однако, дополнительного уточнения, учитывающего присутствие катализатора в двух формах (Nu и RNu), баланс по которым
дает окончательное выражение для скорости реакции:
Обычно бывает так, что скорость одной или двух элементарных стадий пренебрежимо мала по сравнению с остальными, и одним или двумя слагаемыми знаменателя в уравнении (III-4) можно пренебречь. Тогда оно приобретает более простые формы, каждая из которых имеет свои особенности. Всего возможны семь комбинаций слагаемых знаменателя в уравнении (III-4): ся только один член который сокращается с числителем, и в результате для скорости получается уравнение
то в знаменателе остает- Из уравнения (III-3) следует, что. в этих условиях практически весь катализатор находится в свободной форме, скорость лимитируется первой, стадией и реакция имеет нулевые порядки по Z и Y .
Из уравнения (II1-3) следует, что в подобных условиях практически весь катализатор находится в форме каталитического комплекса, скорость лимитируется второй стадией, и на нее не ©лияют концентрации Z и RZ.
Здесь на первой стадии устанавливается равновесие с низкой концентрацией промежуточного комплекса, которая по уравнению (III-3) составит
Скорость лимитируется второй стадией, реакция имеет первые порядки по обоим реагентам и тормозится продуктом. 4. Когда слагаемое знаменателя .двух остальных, получаем уравнение
пренебречь чле-
В этом случае первая стадия практически необратима, а стационарные концентрации двух форм катализатора
5. В знаменателе уравнения (III-4) можно ном
Уравнение (III-9) соответствует медленной реакции катализатора в исходной форме Nil с реагентом RZ н быстрому последующему взаимодействию промежуточного продукта RNu с Z и Y с образованием исходного или конечного продукта. При таком соотношении скоростей реакция тормозится продуктом Z, а катализатор находится преимущественно в исходной форме 6.
Такое уравнение справедливо при лимитировании скорости реакции взаимодействием промежуточного продукта RNu и Y на второй стадии. Согласно уравнению (III-3) при этом условии ганавливается равновесие с близкими значе-
на первой стадии усч ниями концентраций и реакция тормозится продуктом Z. 7. Скорости всех трех элементарных реакций в рассматриваемой схеме соизмеримы, а скорость суммарной реакции описывается уравнением (III-4) в наиболее общей форме. При этом равновесие и а первой стадии ие устанавливается, а соотношение стационарных концентраций [Nu] и l[;RNu]i описывается уравнением (III-4). и представить кинетическое уравнение реакции в таком виде:
Кинетические Закономерности реакции (III-1), протекающей через предварительное образование комплекса YH***ZR за счет водородной связи, не столь разнообразны, поскольку равновесие образования таких комплексов устанавливается всегда быстро. Это позволяет выразить концентрацию комплекса через концентрацию свободных форм реагентов и константу равновесия Совместное решение уравнений скорости н баланса дает общее выражение для скорости реакции, протекающей по схеме (ИМ):
Поскольку катализатор в этой схеме не образует никаких комплексов, общая его концентрация Кинетику гомогенно-каталитических реакций обычно исследуют в периодических условиях, причем объем реакционной смеси остается все время практически постоянным. С целью упрощения кинетических уравнений и лучшего выбора альтернативных вариантов первые серии опытов часто проводят при одинаковой концентрации катализатора н большом избытке одного из реагентов, концентрации которых постоянны и могут вводиться в значения эффективныхконстант. Так, при уравнения:необходимо учитывать только баланс по RZ. Это зна- чительно упрощает уравнение (111-11) и дает:
Уравнения (111-4) — (III-10) при условии избытка Y также преобразуются в одну из четырех более простых форм:
где -функция Су,о, СRZ,o и элементарных констант. Уравнения легко интегрируются, и при графическом изображении результатов опыта в координатах уравнения, преобразованного в линейную форму относительно неизвестных констант, можно оценитьсоответствие уравнений эксперименту и определить значения
дополнительных сериях опытов с варьированием этих величин. В результате устанавливают кинетическое, уравнение и механизм, адекватность которых опыту проверяют по всему массиву экспериментальных данных способами линейного или нелинейного МНК. с одновременным уточнением значений констант. Пример. Кинетику гидролиза хлорпроизводного при катализе тетраметнл- аммониннодидом

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
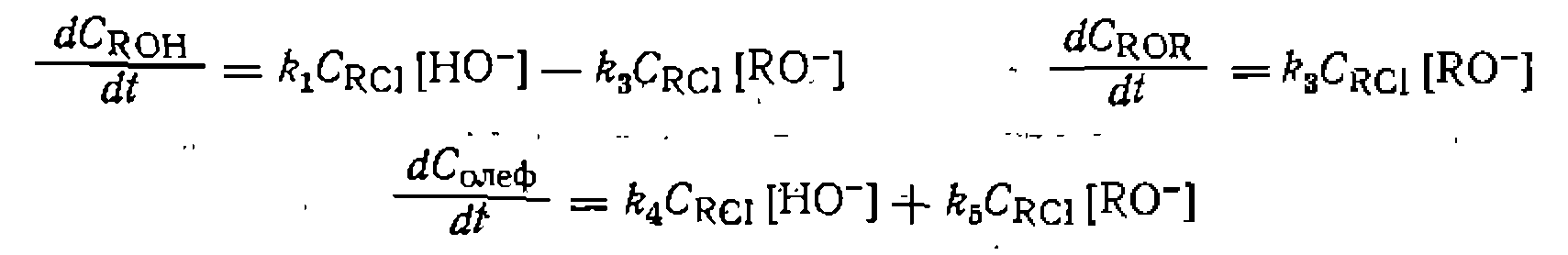
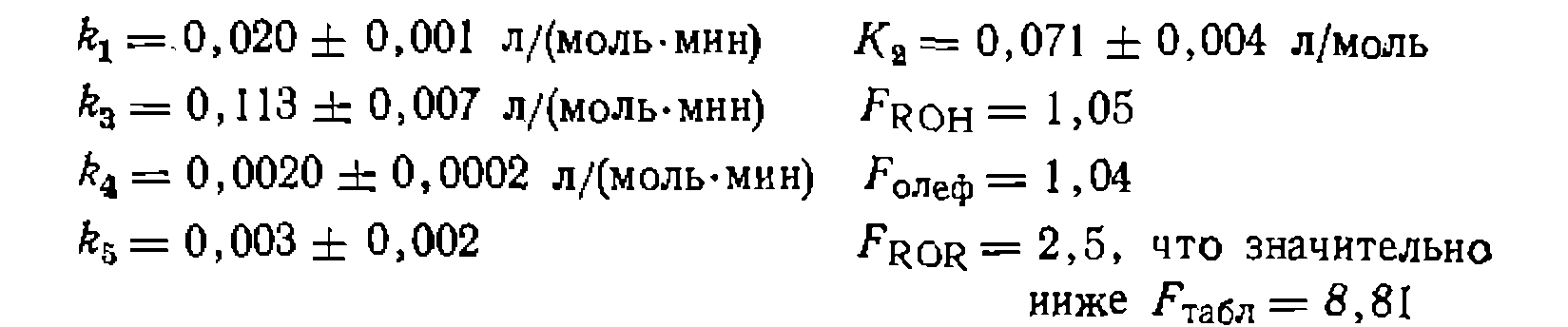
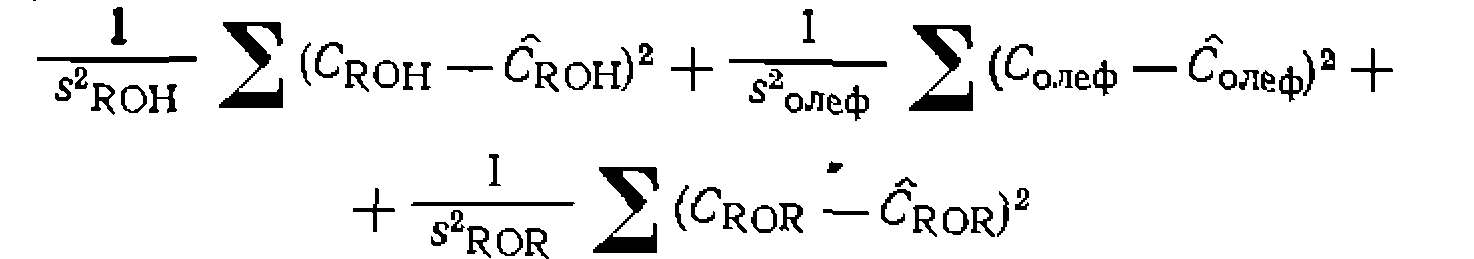
 в пределах доверительного интервала получилась равной нулю, значит, прямой изомеризации орто- и пара-изомеров нет, а есть только 1,2-мнграция алкильной группы. Сравнение найденных констант равновесия с экспериментально определенными показывает их соответствие (по разным данным, /Ci-3,21, 3,33, 4,27, 3,75 н /С2=0,34, 0,33, 0,35, 0,25).
в пределах доверительного интервала получилась равной нулю, значит, прямой изомеризации орто- и пара-изомеров нет, а есть только 1,2-мнграция алкильной группы. Сравнение найденных констант равновесия с экспериментально определенными показывает их соответствие (по разным данным, /Ci-3,21, 3,33, 4,27, 3,75 н /С2=0,34, 0,33, 0,35, 0,25).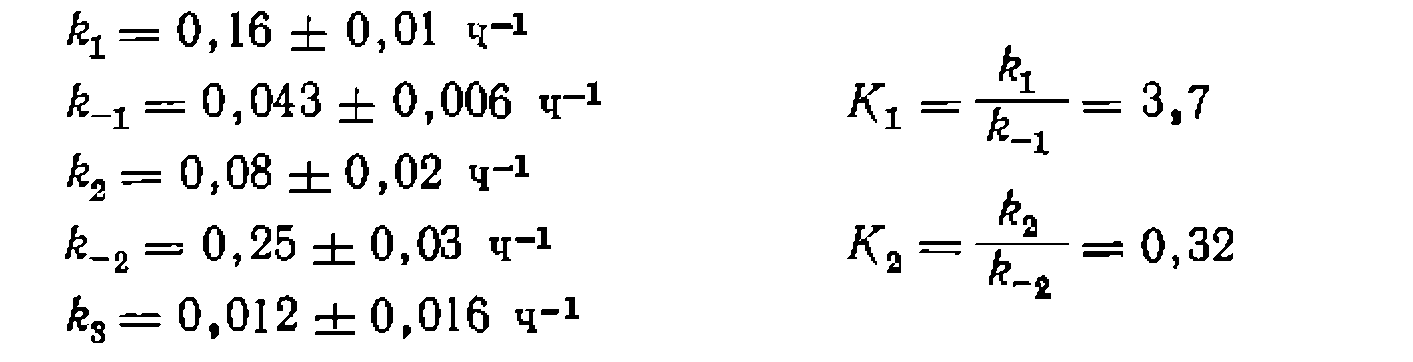
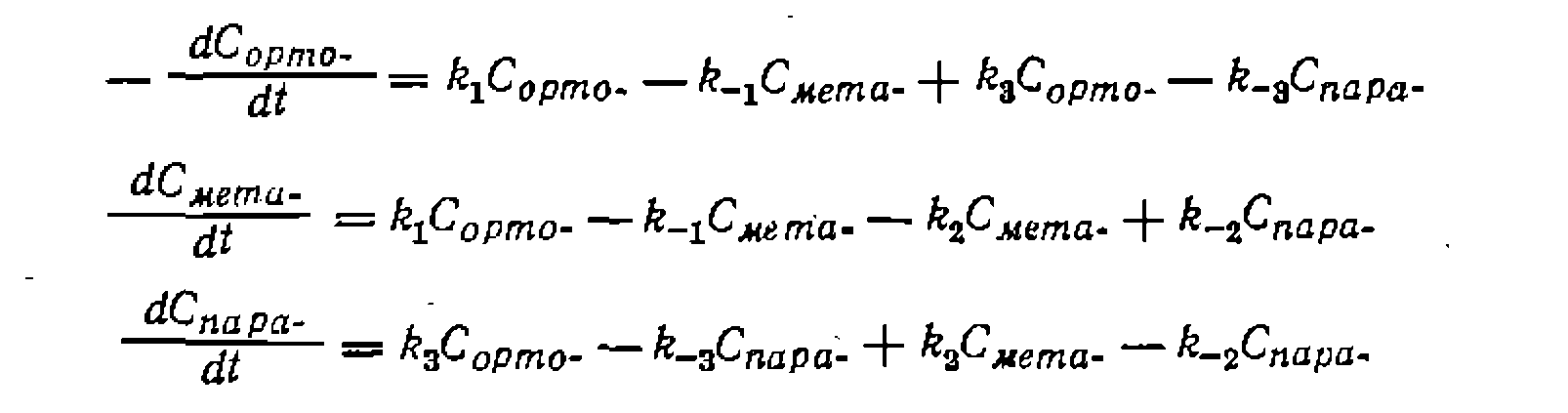
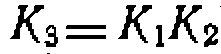 ). Расчет проводим на ЭВМ. путем подбора
). Расчет проводим на ЭВМ. путем подбора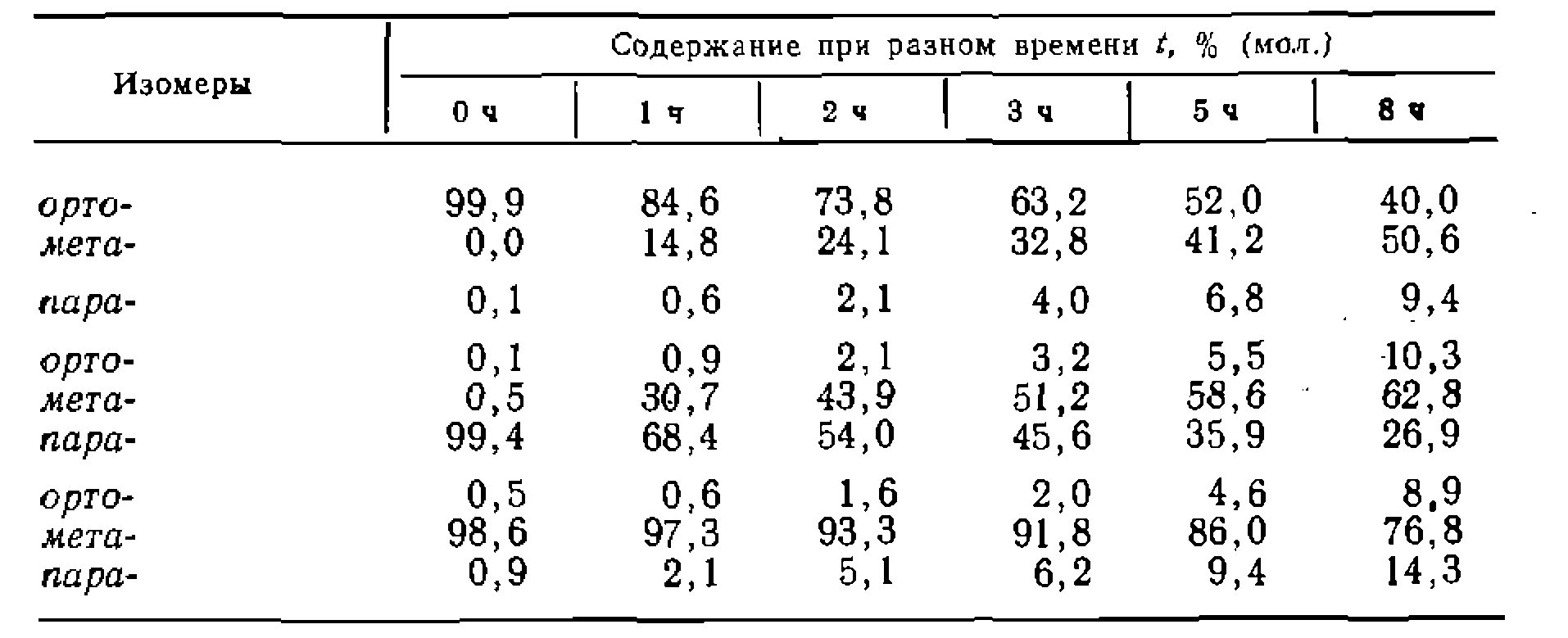
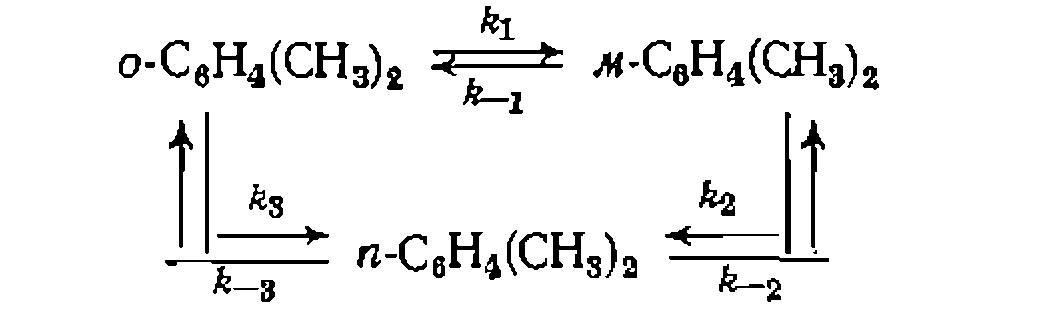
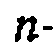 ксилола равны нулю. Тогда система дифферепци- альных уравнении содержала бы только два неизвестных
ксилола равны нулю. Тогда система дифферепци- альных уравнении содержала бы только два неизвестных 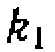 и
и 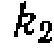 , что существенно упрощает задачу. Соответствие опытов расчетам иллюстрирует рис. 28.
, что существенно упрощает задачу. Соответствие опытов расчетам иллюстрирует рис. 28.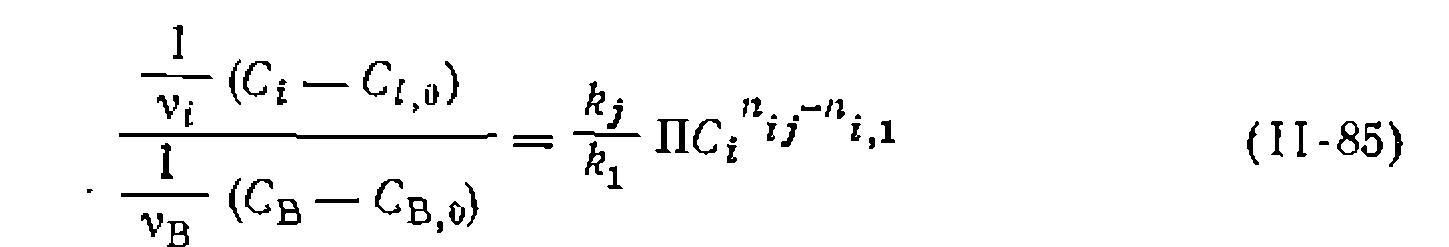
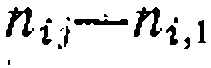
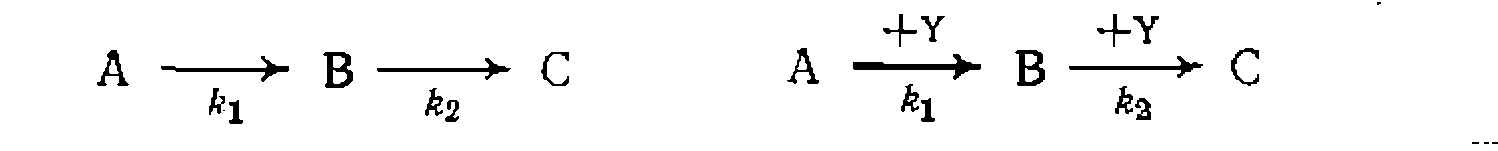
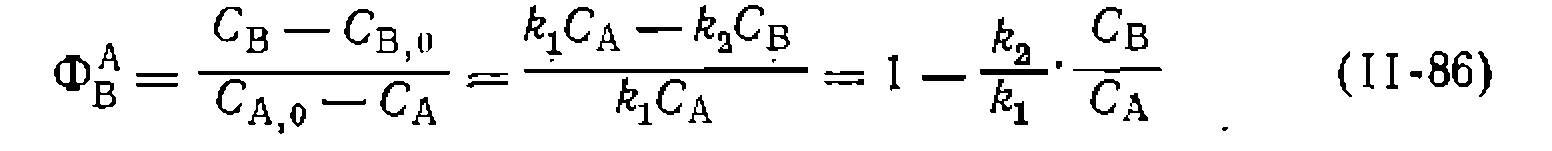
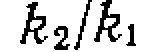

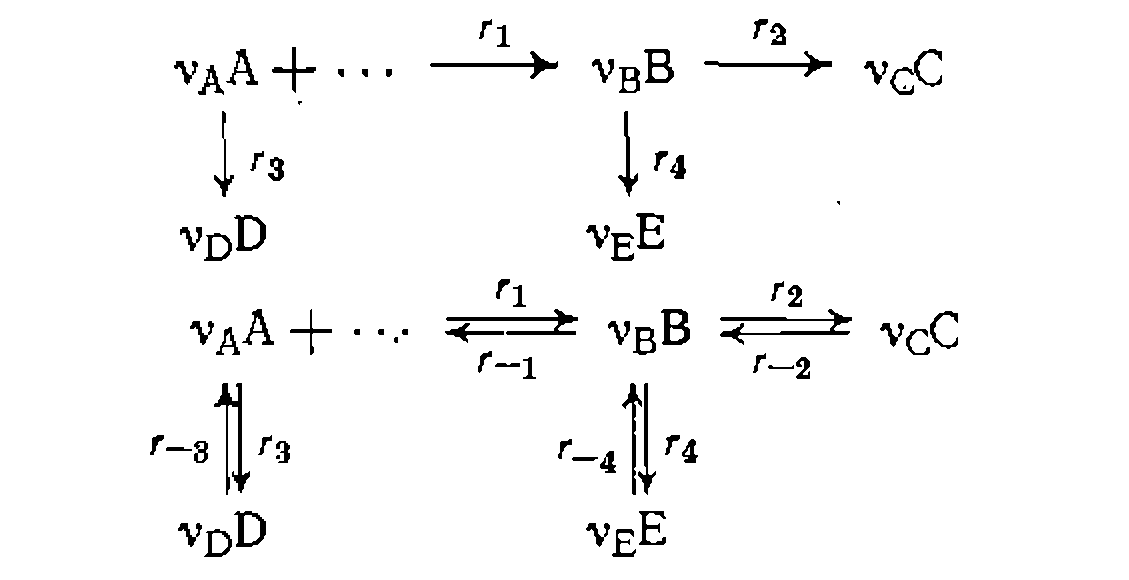
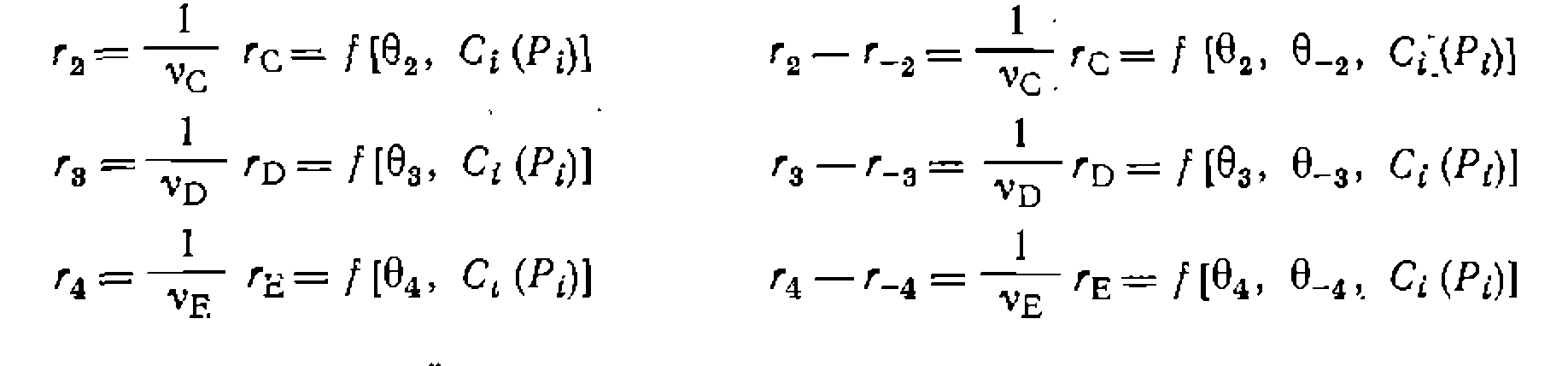
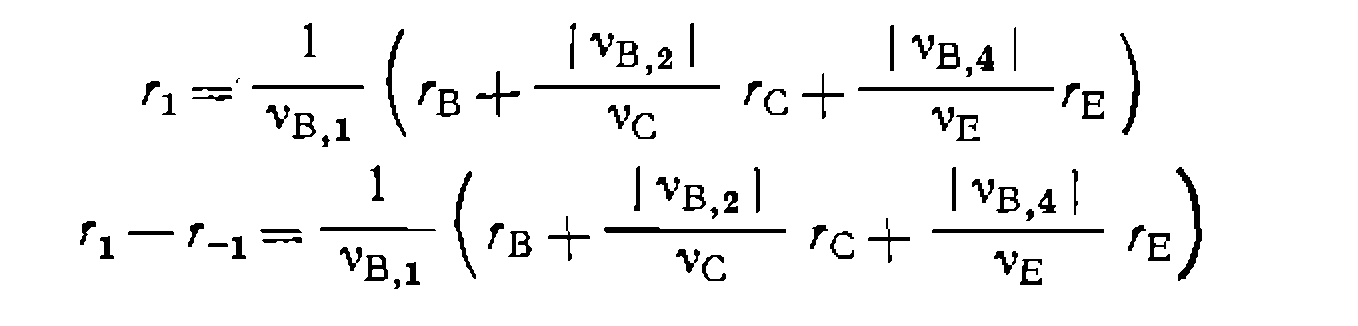
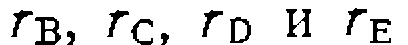 вычис
вычис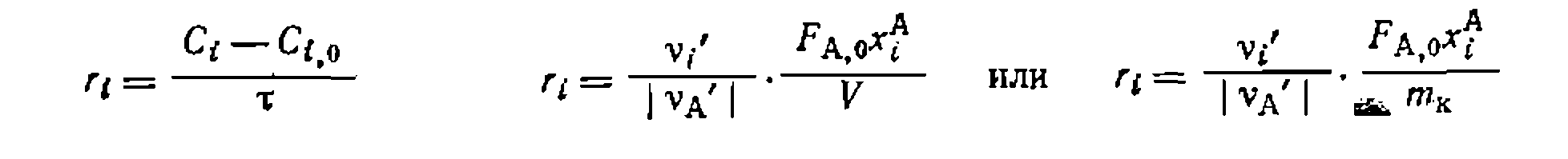
 являются функциями
являются функциями  и
и 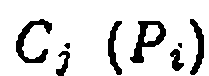 . Оче
. Оче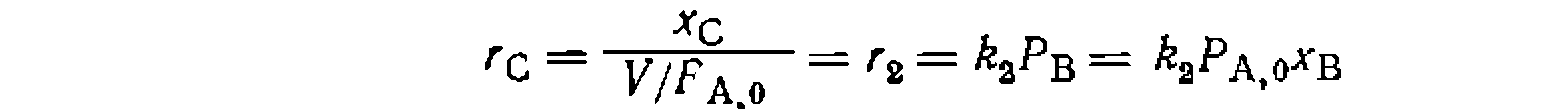

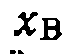 и
и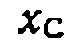 равнялось ±0,001.
равнялось ±0,001.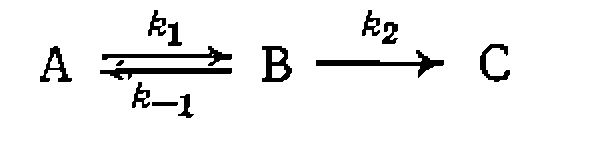
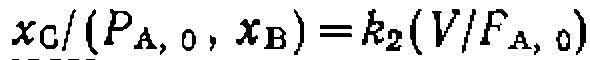 . Поиск константыведем с
. Поиск константыведем с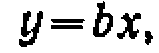 где
где 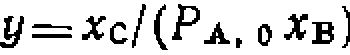 1,
1,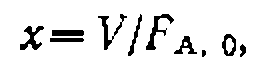 что дает
что дает 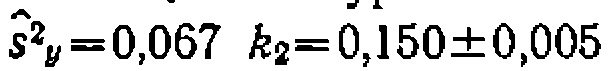 моль/(л*мин-МПа)
моль/(л*мин-МПа)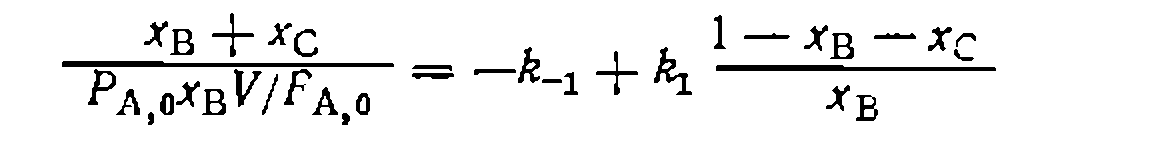
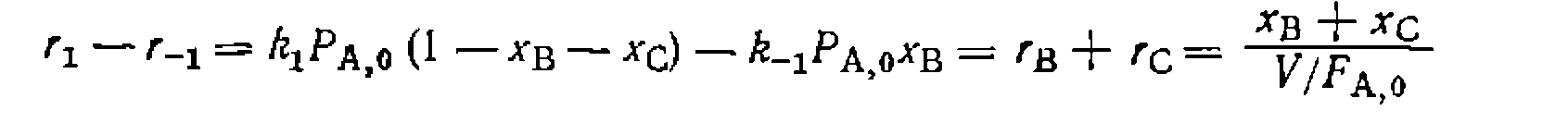
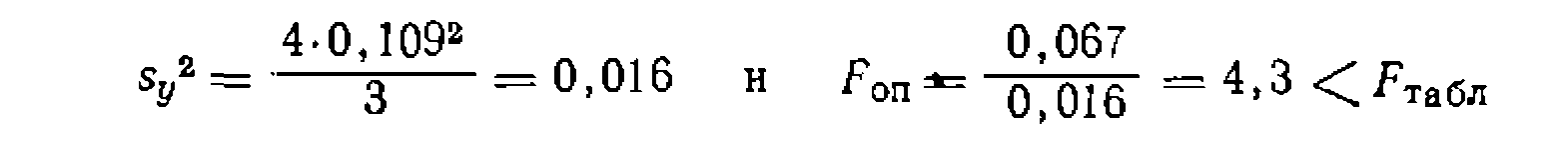
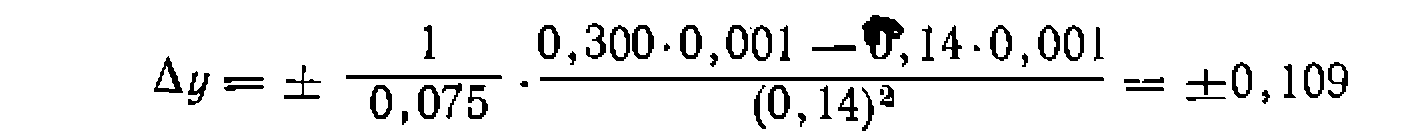
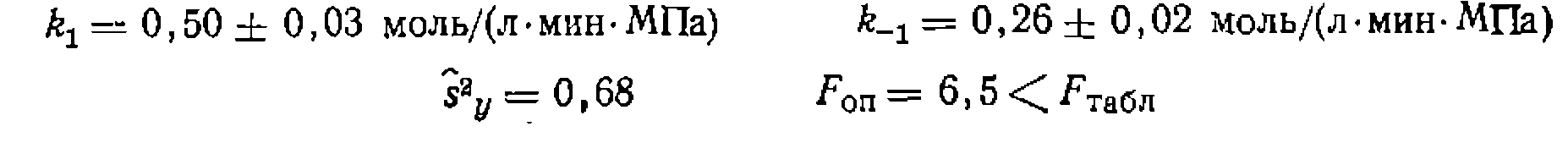
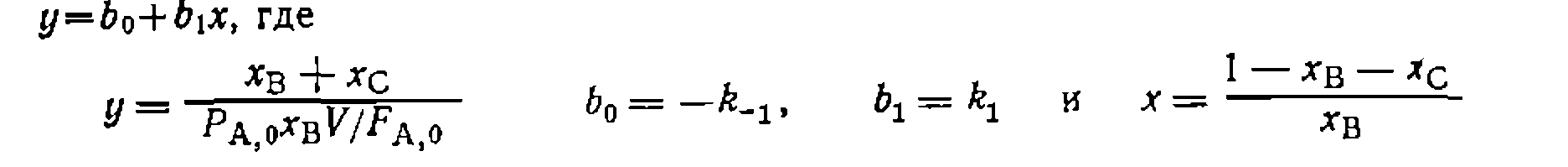
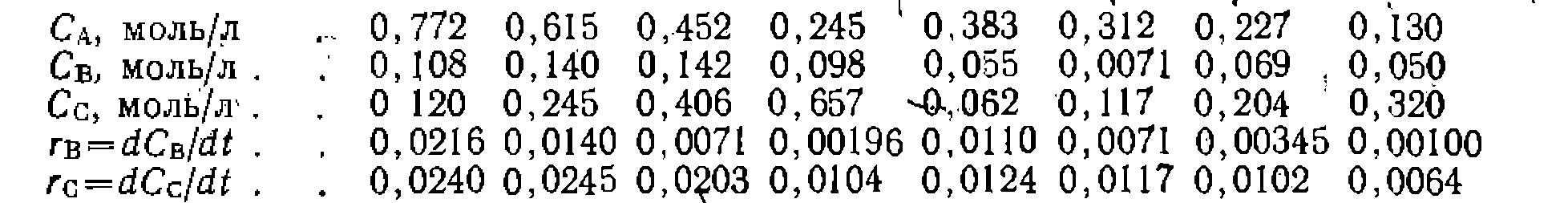
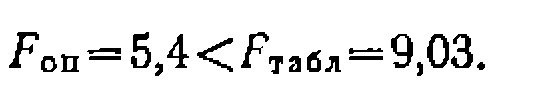
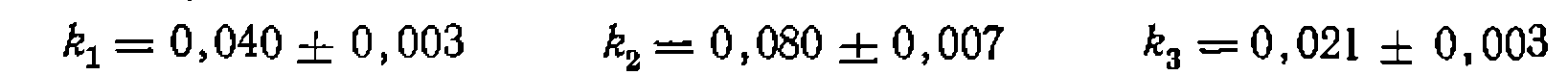
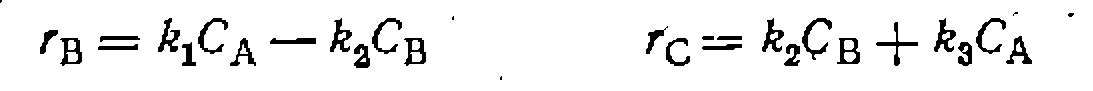
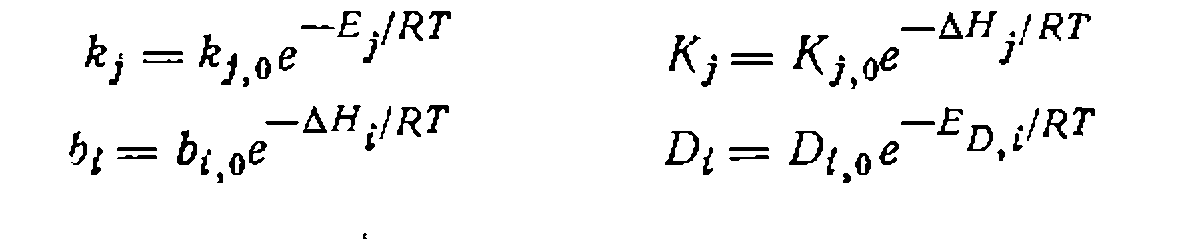
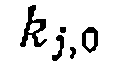 и
и 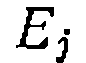 —предэкспоненциальный множитель и энергия активации химической реакции (когда
—предэкспоненциальный множитель и энергия активации химической реакции (когда  является комбинацией констант, то эти величины не истинные, а эффективные),
является комбинацией констант, то эти величины не истинные, а эффективные), 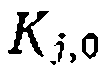 и
и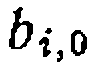 — постоянныеинтегрирования, не имеющие физического смысла,
— постоянныеинтегрирования, не имеющие физического смысла, 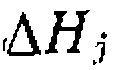 и
и 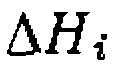 —энтальпии реакций, адсорбции и др., а
—энтальпии реакций, адсорбции и др., а 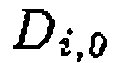 и
и  —предэкспоненциальный множитель и энергия активации диффузии.
—предэкспоненциальный множитель и энергия активации диффузии.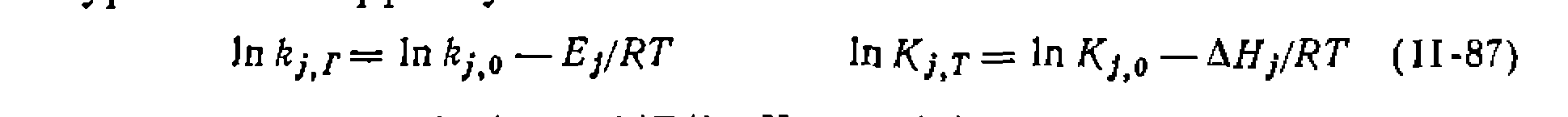
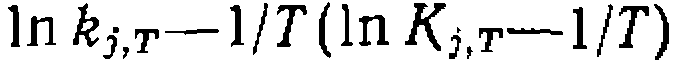 они дают линейную за
они дают линейную за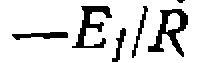 или
или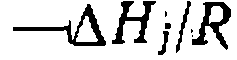 . Расчет
. Расчет 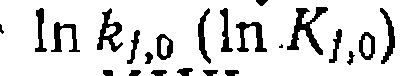 и
и 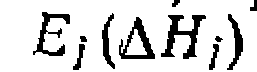 осуществляют при
осуществляют при . Ранее уже говорилось, что в уравнениях типа уравнения Аррениуса пред- экспонента и энергетический параметр обычно сильно закорре- лированы. Поэтому предпочтительно обрабатывать полученные данные на ЭВМ с помощью нелинейного МНК, находя
. Ранее уже говорилось, что в уравнениях типа уравнения Аррениуса пред- экспонента и энергетический параметр обычно сильно закорре- лированы. Поэтому предпочтительно обрабатывать полученные данные на ЭВМ с помощью нелинейного МНК, находя 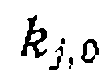
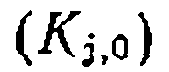 и
и 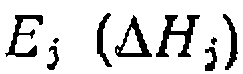 по минимуму взвешенной суммы квадратов
по минимуму взвешенной суммы квадратов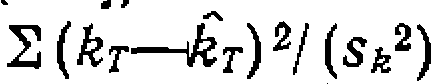 . Доверительные интервалы иско
. Доверительные интервалы иско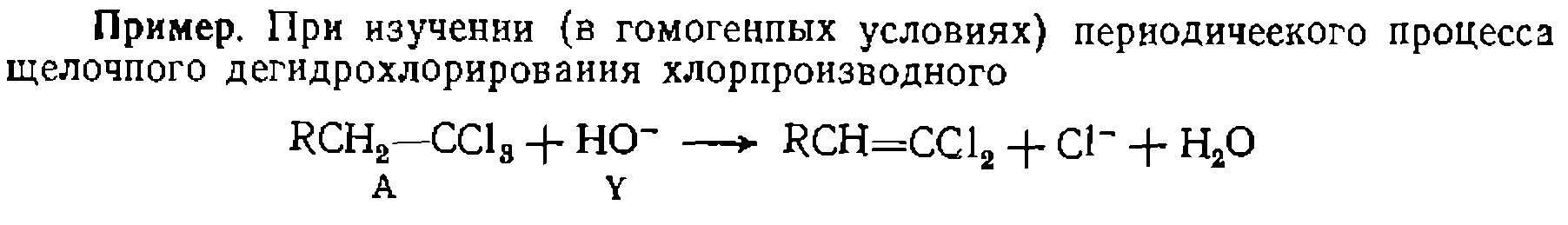
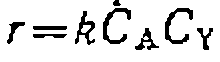 и значение
и значение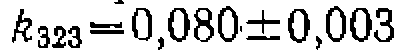 л/1 (моль•мин’). После- этого были про
л/1 (моль•мин’). После- этого были про моль/л,
моль/л,
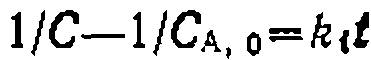 были найдены следующие значения констант:
были найдены следующие значения констант: 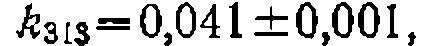
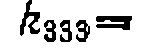

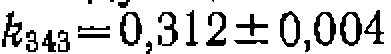 . Их представление в координатах уравнения Аррениуса приведено на рис. 29. Активационные параметры находят по линейному МНК с минимизацией суммы квадратов отклонений в
. Их представление в координатах уравнения Аррениуса приведено на рис. 29. Активационные параметры находят по линейному МНК с минимизацией суммы квадратов отклонений в 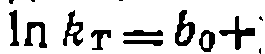
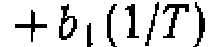 . В результате получаем:
. В результате получаем: 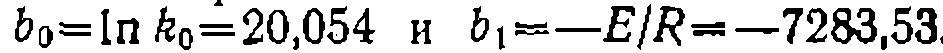
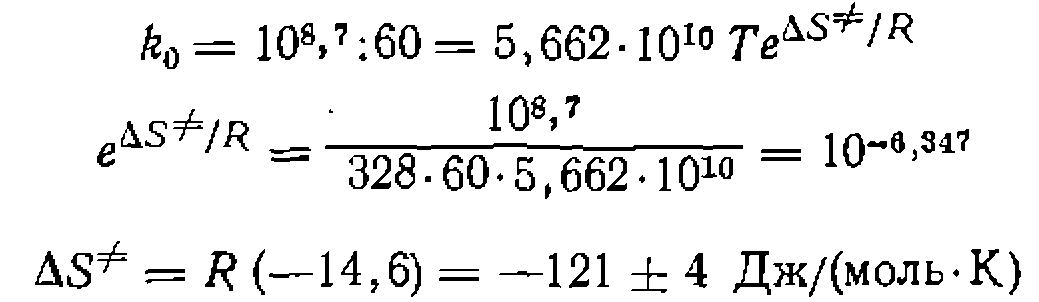
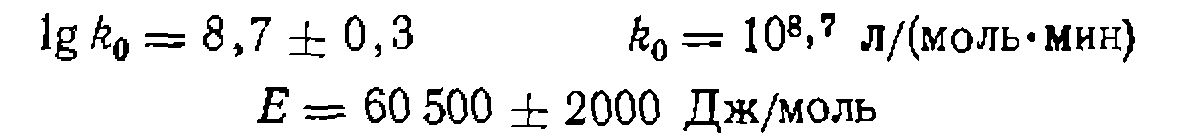
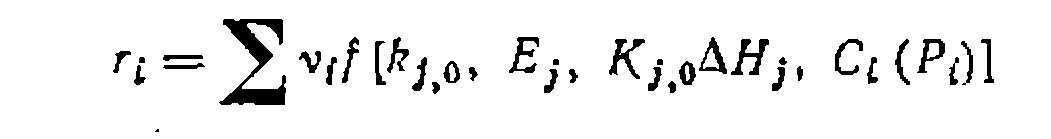
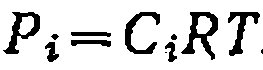
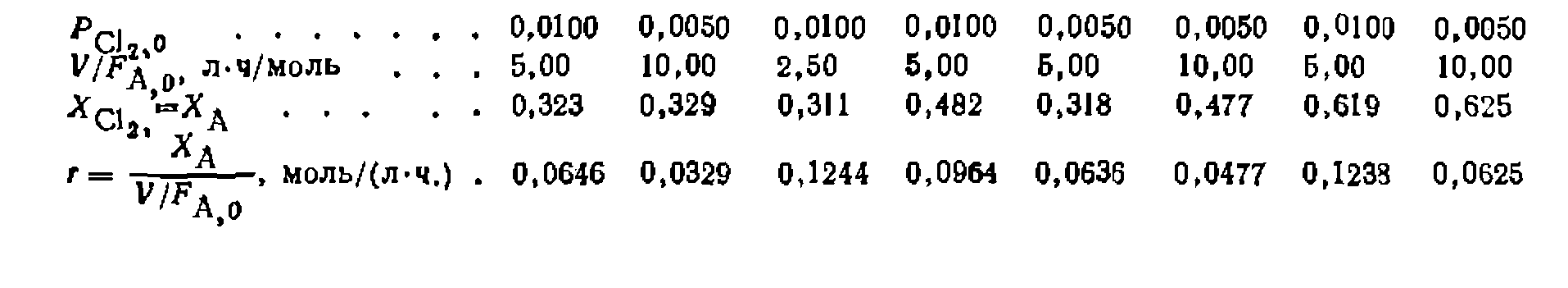
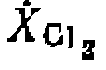
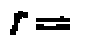
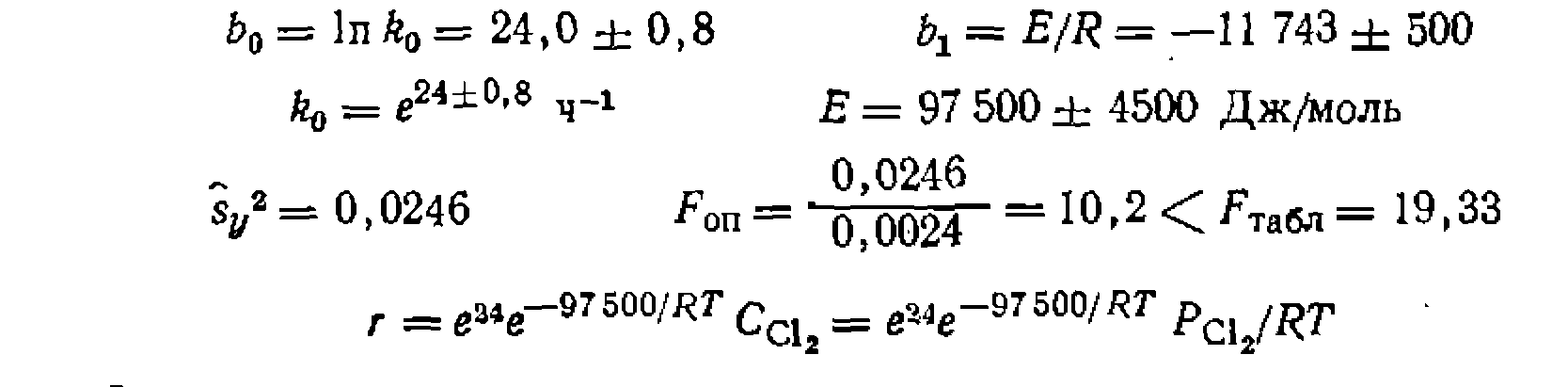
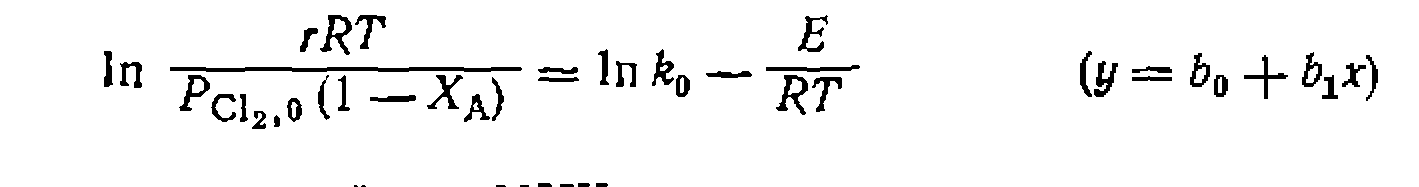
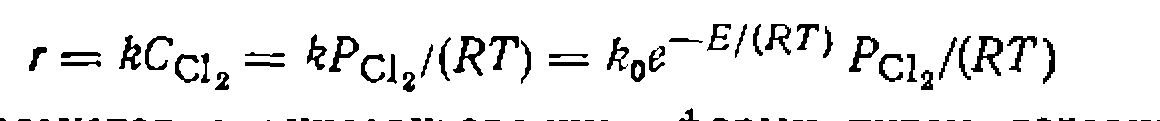
 . При избытке углеводорода оно превращается в уравнение нер- вого порядка
. При избытке углеводорода оно превращается в уравнение нер- вого порядка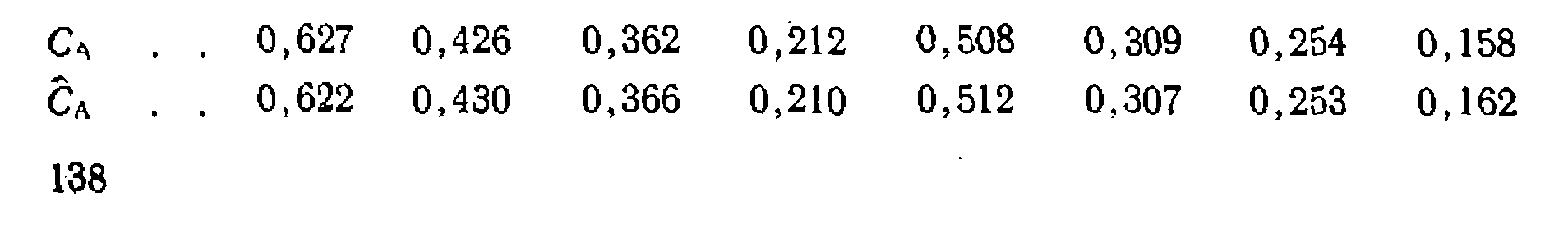
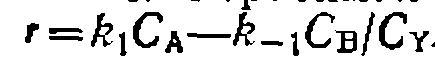 . Считая, что константа равновесия
. Считая, что константа равновесия 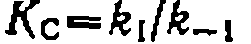 известна,
известна,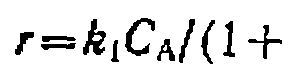
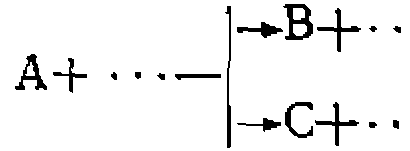
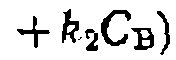 . Найдите его интегральное решение и преобразуйте последнее в линейную форму для обработки опытов, проведенных в периодических условиях.
. Найдите его интегральное решение и преобразуйте последнее в линейную форму для обработки опытов, проведенных в периодических условиях.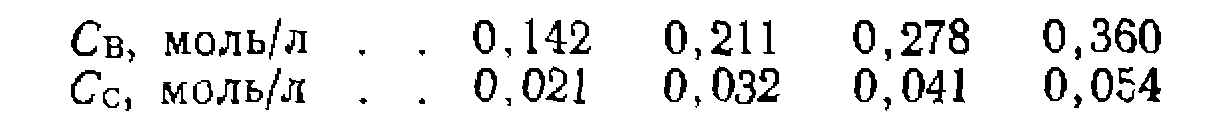
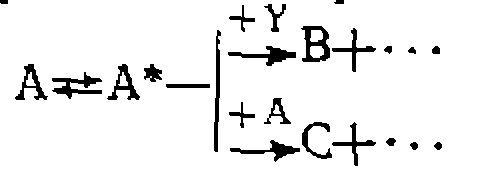
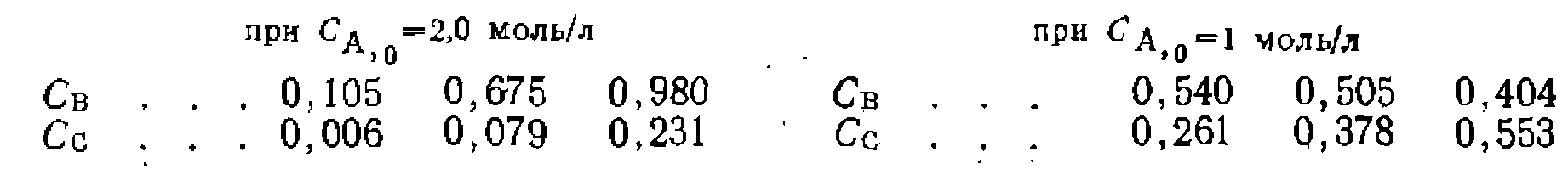
 : '
: '
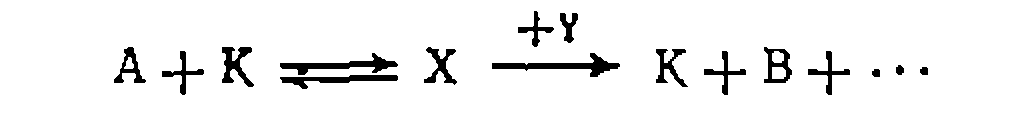
 , оксианионы
, оксианионы 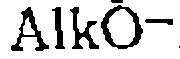
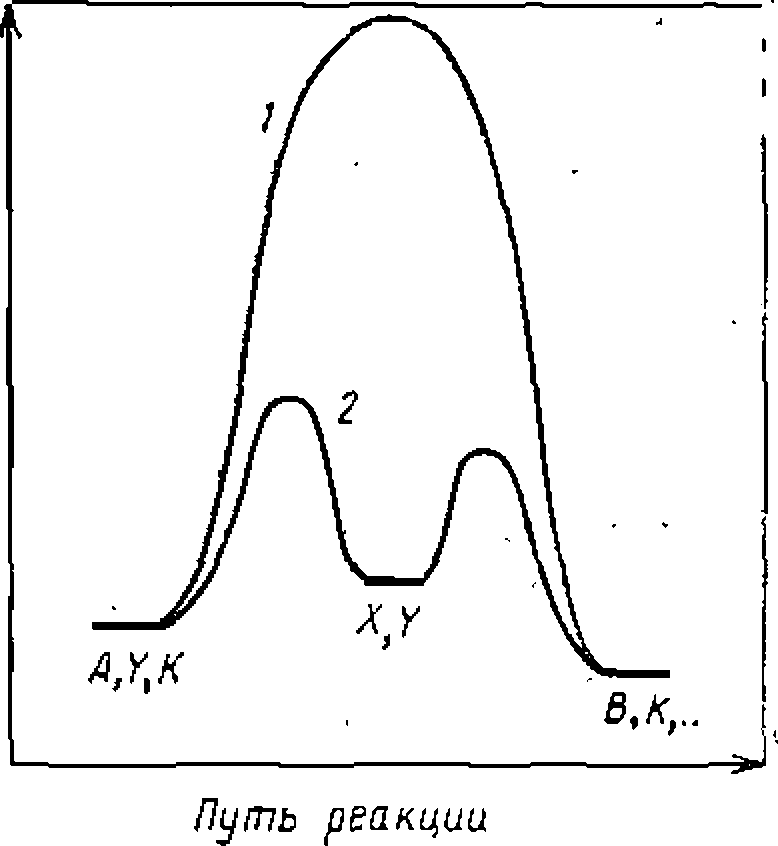
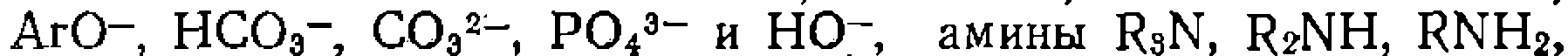
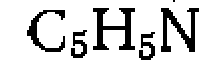 и
и 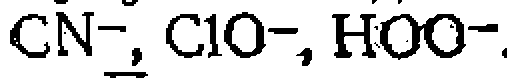 имидазол, а также некоторые другие анионы —
имидазол, а также некоторые другие анионы — 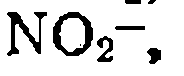
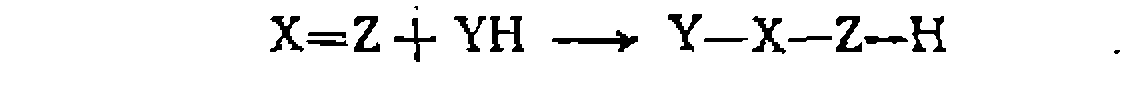
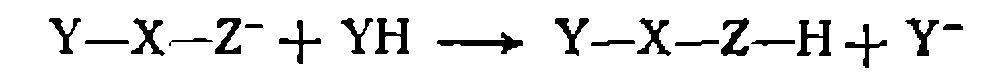
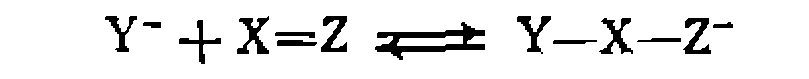

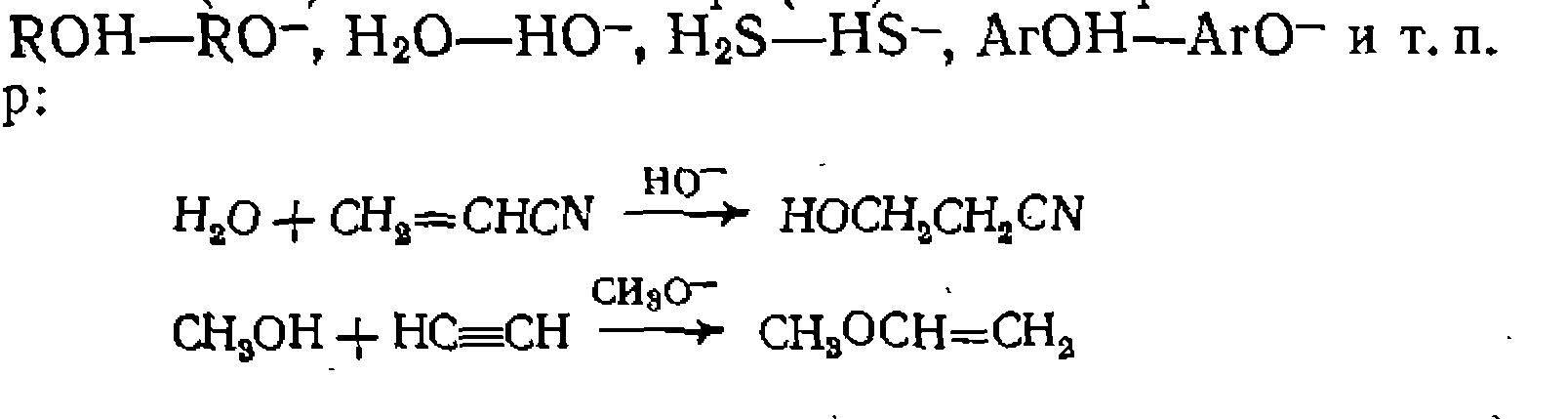
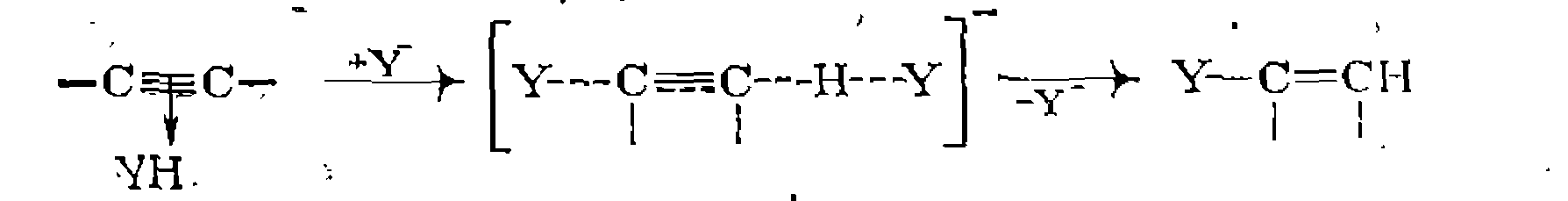
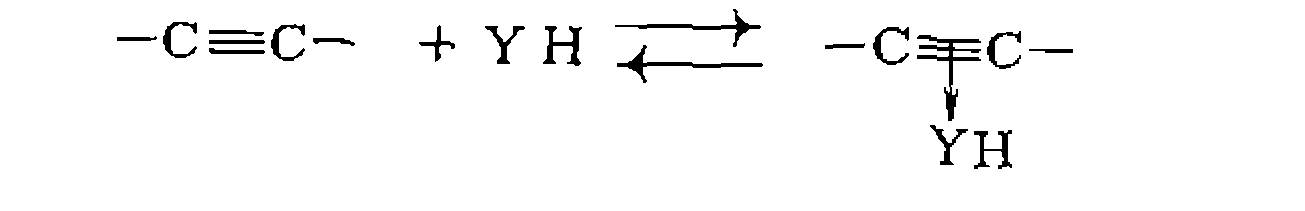
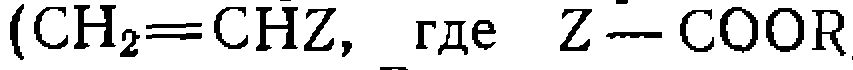 ,,
,, и к ацетиленам. В этих реакциях кратная связь активируется образованием я-комплекса YH с реагентом:
и к ацетиленам. В этих реакциях кратная связь активируется образованием я-комплекса YH с реагентом:
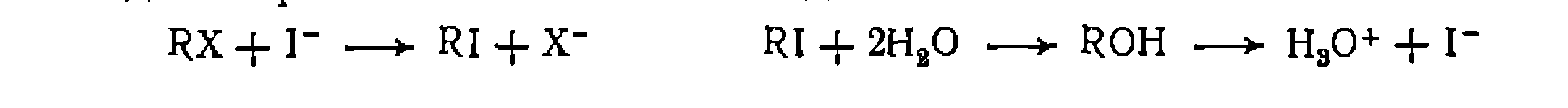

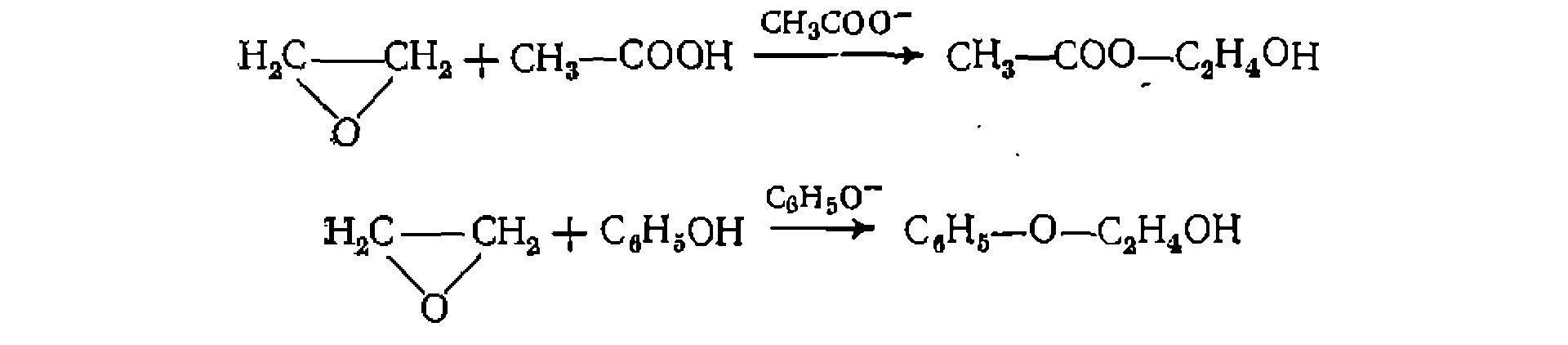
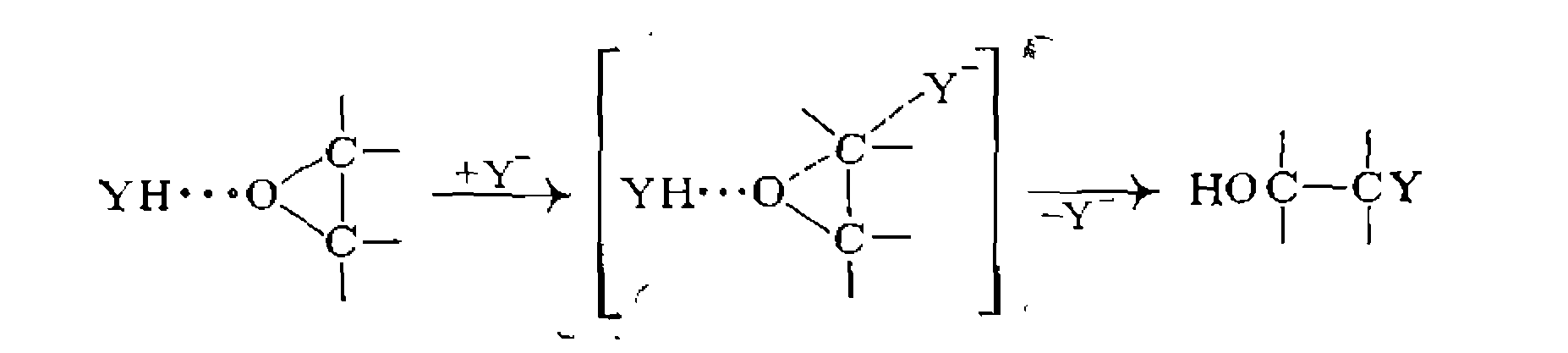
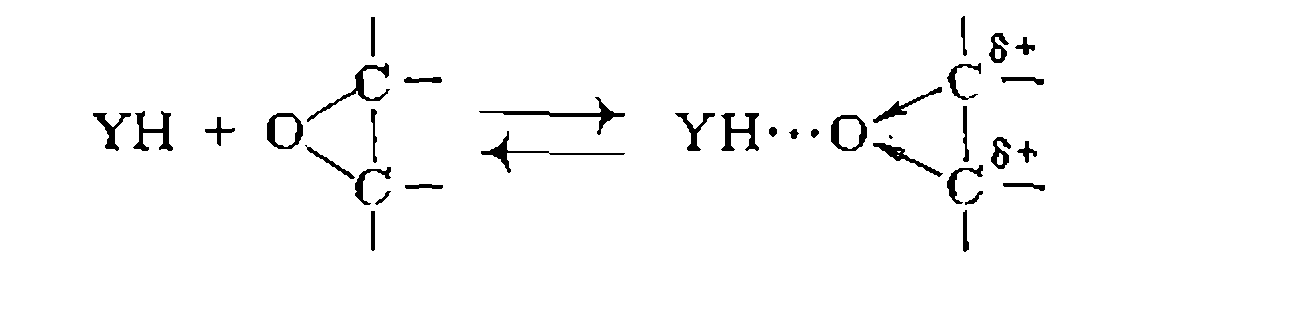
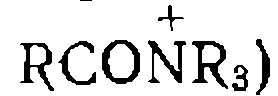 — одного из самых эффективных ацилирующих агентов благодаря сильным электроноакцепторным свойствам чет-
— одного из самых эффективных ацилирующих агентов благодаря сильным электроноакцепторным свойствам чет-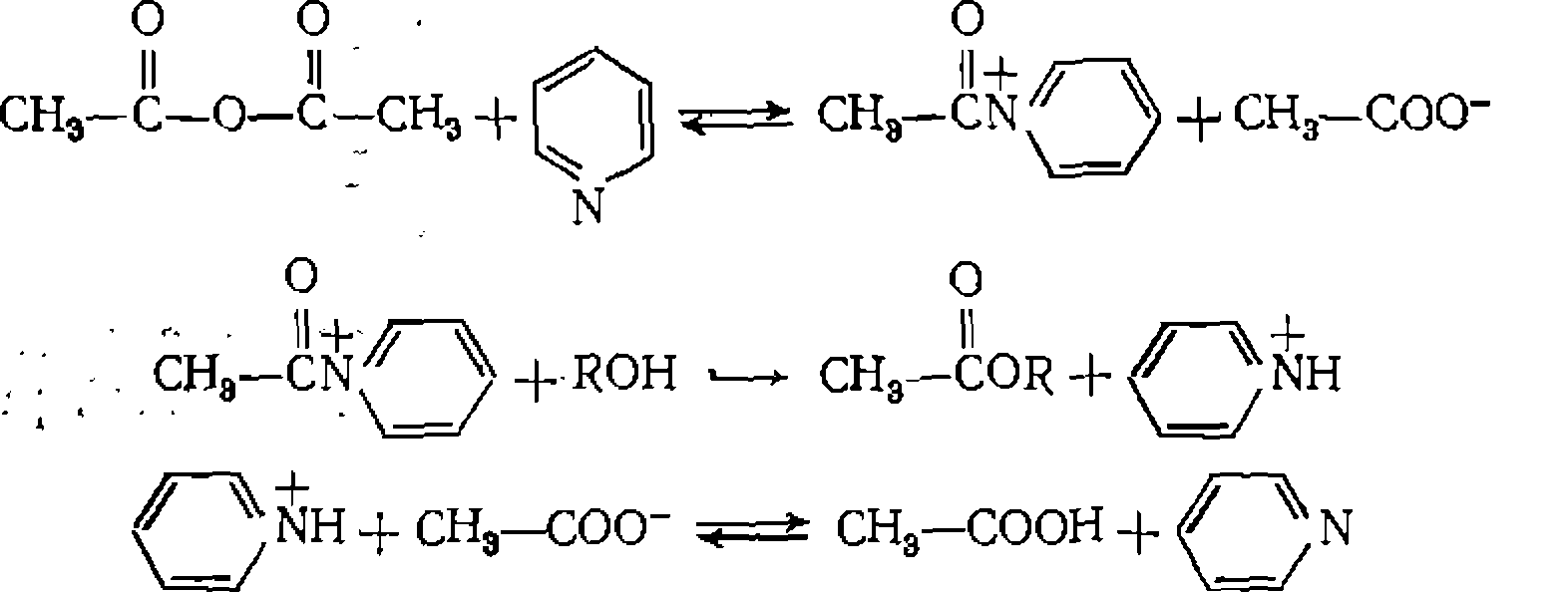
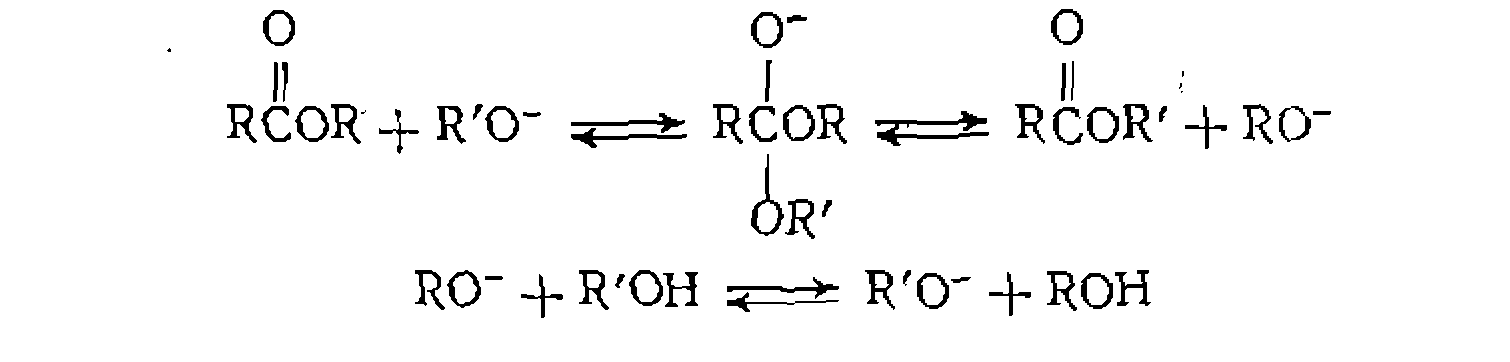

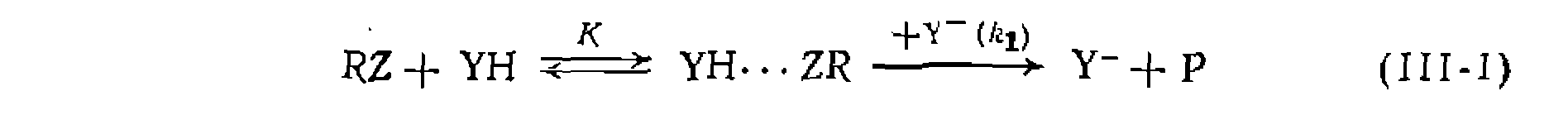
 . образуетсяпрн взаимодействии катализатора
. образуетсяпрн взаимодействии катализатора 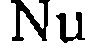 с одним из реагентов
с одним из реагентов 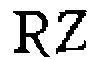 , а образование продукта и< регенерация катализатора происходят в результате последующих превоашений комплекса:
, а образование продукта и< регенерация катализатора происходят в результате последующих превоашений комплекса: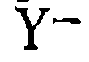 и образование продукта
и образование продукта  :
: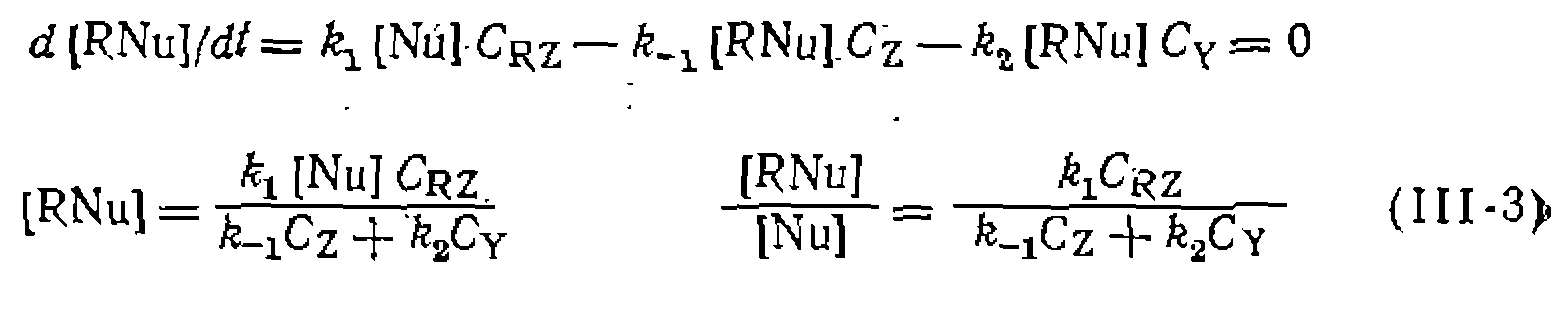
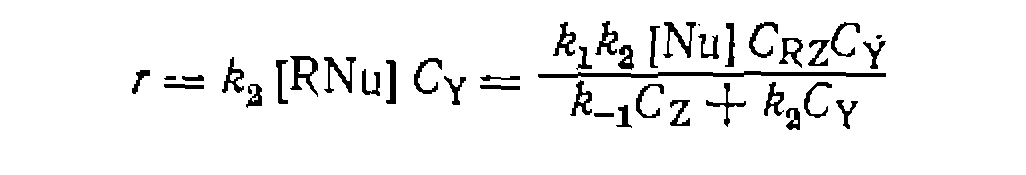
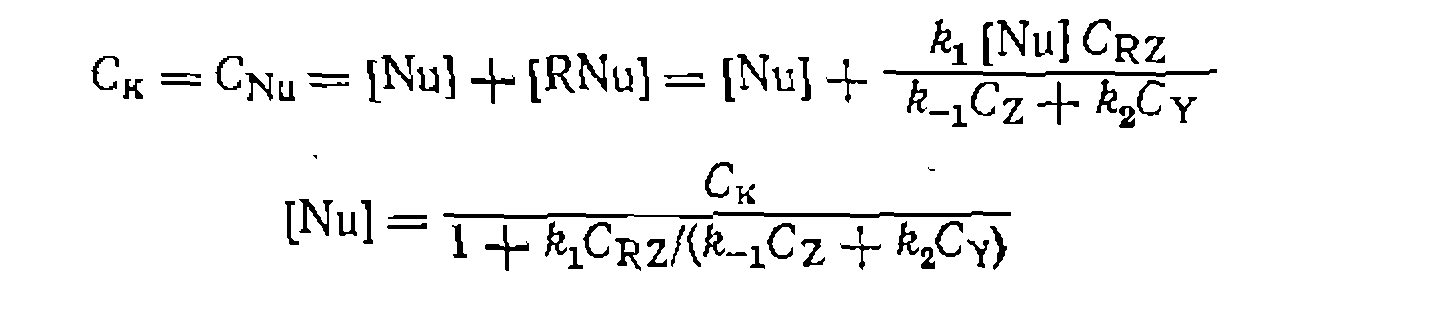
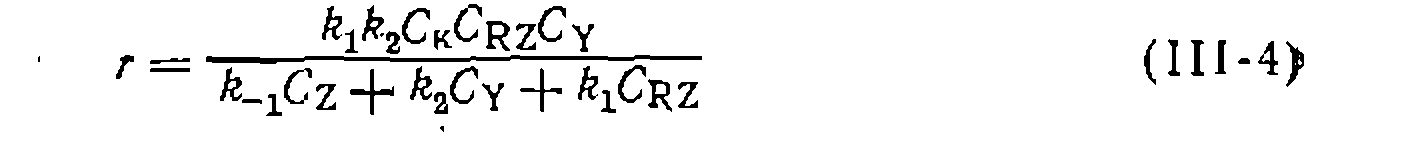
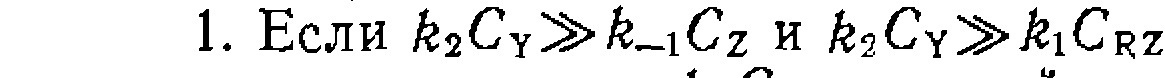

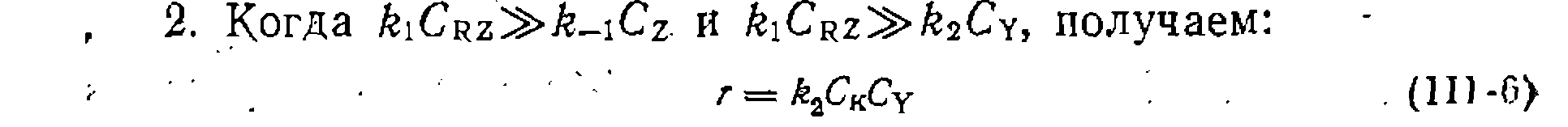
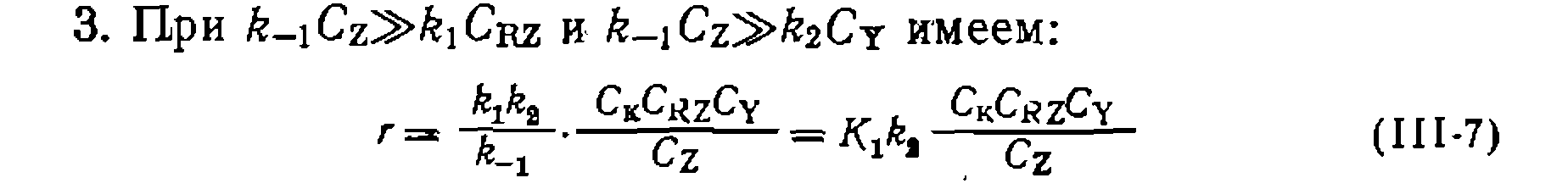
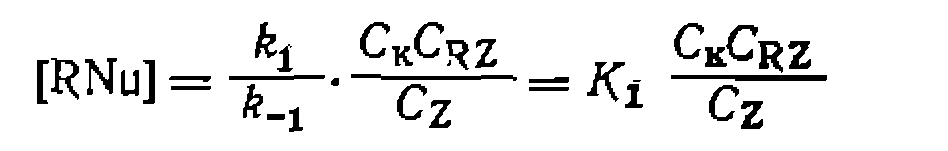
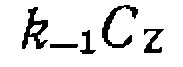 значительно меньше
значительно меньше
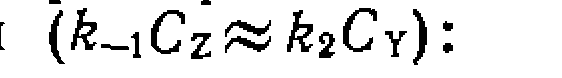
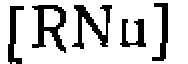 и i[Nu]| можно найти из условия равенства скоростей первой и второй стадий:
и i[Nu]| можно найти из условия равенства скоростей первой и второй стадий:
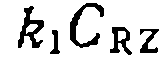 , а остальные слагаемые соизмеримы
, а остальные слагаемые соизмеримы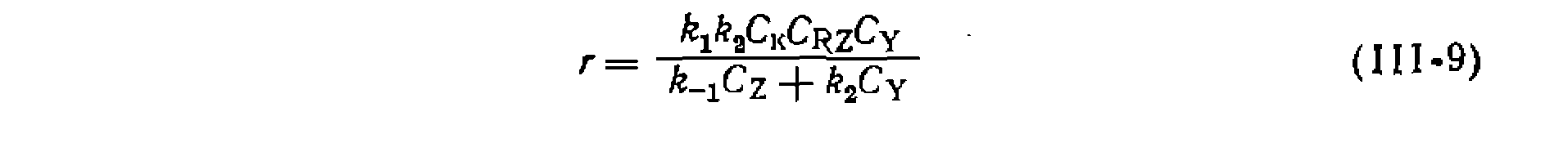
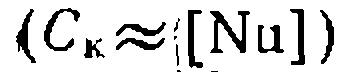 Наименьшее значение в знаменателе уравнения (111-4)’ принимает слагаемое
Наименьшее значение в знаменателе уравнения (111-4)’ принимает слагаемое 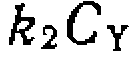 , а два других соизмеримы:
, а два других соизмеримы: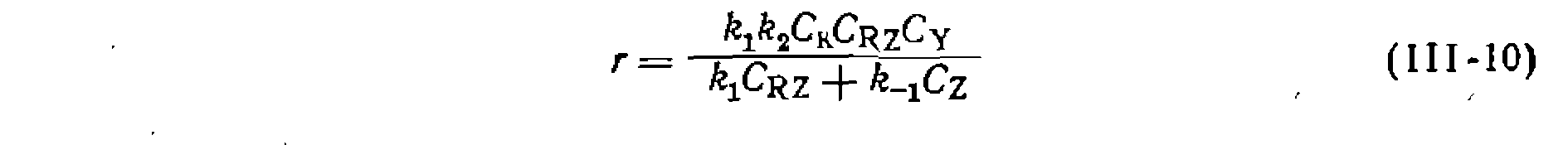
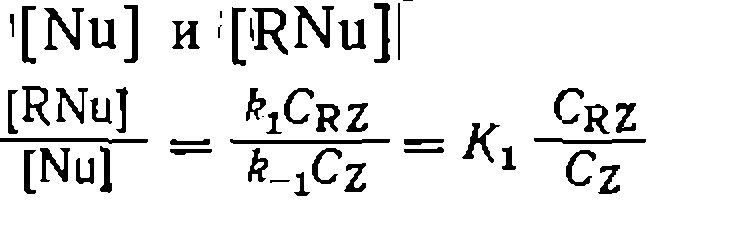
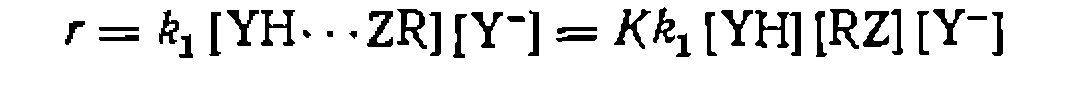
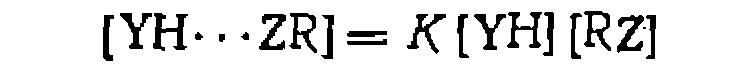
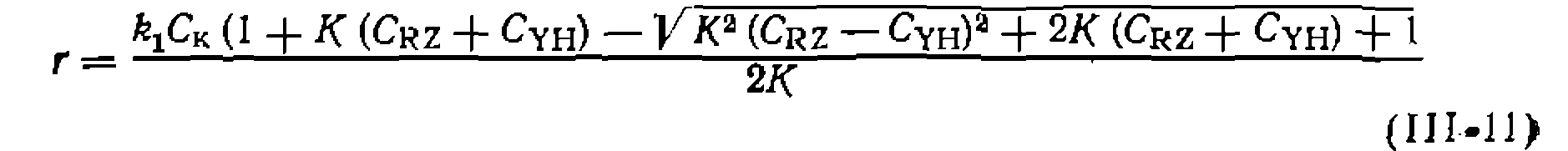
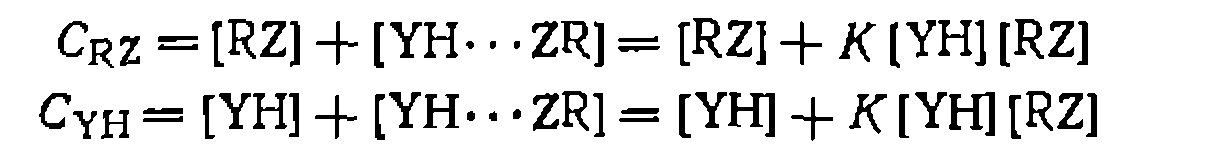
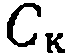 равна концентрации Y-, а для выражения концентраций свободных форм реагентов через их суммарные или аналитические концентрации необходимо учесть комплексообразование между ними: ■ .
равна концентрации Y-, а для выражения концентраций свободных форм реагентов через их суммарные или аналитические концентрации необходимо учесть комплексообразование между ними: ■ . можно полагать, что
можно полагать, что 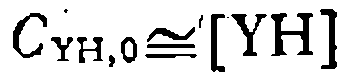 , и при выводе последнего
, и при выводе последнего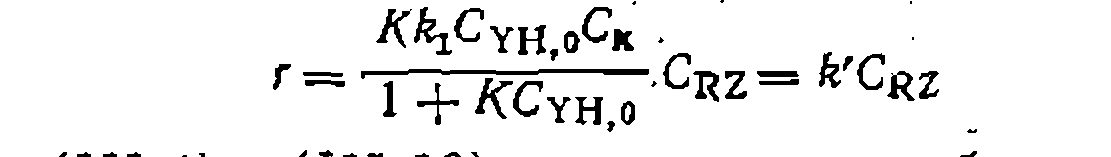
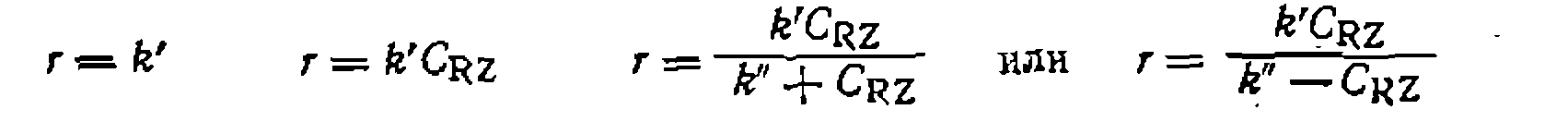
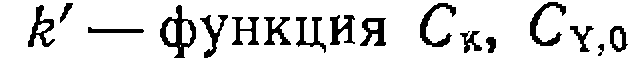 и элементарных констант, а
и элементарных констант, а 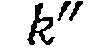 —
—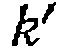 и
и Зависимость последних от
Зависимость последних от 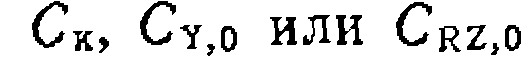 проверяют в
проверяют в