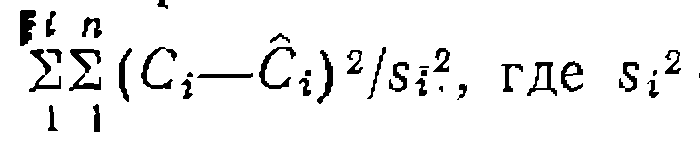|
|
ОСНОВЫ ОБРАБОТКИ КИНЕТИЧЕСКИХ ДАННЫХПосле выдвижения гипотезы о механизме реакций и построения из нее кинетических уравнений или кинетической модели ' процесса наступает следующий этап исследования, состоящий в обработке ранее полученных экспериментальных данных в такой последовательности: 1) нахождение численных значений параметров (констант) кинетических уравнений или модели; 2) проверка адекватности уравнений эксперименту; 3) проверка других гипотез о механизме реакций и выведенных из них моделей, дискриминация других гипотез; •4) нахождение доверительных интервалов найденных параметров (констант) уравнений, адекватных эксперименту. Нахождение параметров уравнений основано на принципе максимума правдоподобия, согласно которому наилучшими оценками параметров являются те, которые при подстановке в уравнения (вместе с параметрами процесса в каждой опытной точке) обеспечивают наибольшую сходимость расчетных значений с экспериментальными данными. Максимум функции правдоподобия при нормальном законе распределения ошибок достигается при минимуме взвешенной суммы квадратов отклонений между экспериментальными и вычисленными Значениями концентраций или выходов. Дисперсия большей частью неизвестна, поэтому ее считают постоянной, минимизируя простую сумму квадратов отклонений, т. е. ∑(Сi—Сi)2. Следовательно, поиск констант уравнений сводится к методу наименьших квадратов (МНК), который имеет две разновидности: линейный и нелинейный МНК. Решения кинетических уравнений обычно нелинейны в отношении своих констант, поэтому при использовании линейного МНК уравнения преобразуют в линейную форму:
.Здесь у — некоторая функция, х— параметры процесса или их функции, называемые независимыми переменными, abi— искомые параметры (константы) уравнений. Поиск констант ведут по уравнению (II-58), минимизируя суммы квадратов отклонений найденных и вычисленных значений функции у (т. е. min∑(yi—yt)2). Так, для реакции первого порядка в периодических услгшиях имеем
что дает линейную форму уравнения InCA,o/CA=kt,где у= = 1пСА,о/СА и xi = t.
Поиск констант по линеаризованным формам уравнений с ■одной, или двумя неизвестными константами можно осуществить вручную, т. е. на клавишных машинах или на электронных микрокалькуляторах, но лучше на цифровых ЭВМ. Для уравнений с -одной константой (y=biXi)ее находят по уравнению MHK: где знaк 2 означает, как и прежде, суммирование по всем экспериментальным точкам. Следовательно, при.обработке опытов этим методом для каждой экспериментальной точки рассчитывают функции у их, находят величины, содержащиеся в уравнениях (11-59) или (II-60) и (II-61), суммируют их н определяют соответствующие константы (пример такого расчета дан в этом разделе ниже).
Другая, более общая и распространенная форма обработки опытов по линейному МНК, особенно при использовании цифровых ЭВМ, состоит в применении методов матричной алгебры. Составляют матрицу-столбец Y, где представлены вычисленные из опытов значения функций у В последней матрице единица означает коэффициент при bо в общей форме уравнения y= a0b0+a1b1...... а р — число параметров (констант). где ХT — транспонированная матрица X—>XTX— так называемая информационная матрица, а (ХТХ)-1 — матрица ошибок. Очевидно, что решение для уравнений с одной и двумя константами аналогично приведенному в формулах (II-59), (Д-60) к (11-61). Пример такого способа поиска констант дан в этом разделе ниже.
Описанный способ поиска констант по линеаризованным формам уравнений не имеет строгого обоснования и может дать оценки констант, смещенные относительно их истинных значений. Это объясняется тем, что их находят по минимуму суммы квадратов отклонений некоторых функций у, а не концентраций или выходов, непосредственно находимых из опытов. Очевидно* что в функциях у и х могут накапливаться ошибки, и это может привести к искажению истинных зависимостей и смещению- в оценках констант. Известны случаи, когда, применение линеаризованных форм уравнений приводило к спорным или даже неверным выводам. Тем не менее метод линеаризации широко распространен, и его применение часто оправдывается для более простых форм кинетических уравнений, когда смещение констант не превышает допустимой величины. Для сложных типов кинетических уравнений или моделей,, которые невозможно преобразовать в линейную форму, или для нахождения несмещенных оценок констант ведут обработку опытов по нелинейному МНК, добиваясь минимизации суммы квадратов отклонений экспериментальных и расчетных значений концентраций или выходов, т. е. min∑(Ci—C-i)2или min∑(xi—Xi)2. Принцип поиска параметров уравнений по нелинейному МНК можно проиллюстрировать на примере уравнения с одной: неизвестной константой, как в предыдущем случае реакции первого порядка, когда интегральное выражение lnСA,о1СA = Ш легко преобразуется в вид, разрешенный относительноСA, т. е. СA=СA,oe-kt.Приблизительно оценивают величину kи по этому уравнению, подставляя в него параметры СA,о и tдля каждой экспериментальной точки, находят расчетные значения СA. Затем находят отклонения между экспериментальными и рассчитанными концентрациями СА—СA, их квадраты и сумму квадратов отклонений ∑(СA—СA)2. Такой же расчет повторяют при
других значениях k.В результате получается график (рис. 13, а), в котором минимум суммы квадратов отклонений соответствует оптимальной величине константы скорости (пример такого расчета дан в этом разделе ниже). При наличии в исходном уравнении двух констант их оптимальные значения соответствуют глобальному минимуму, равному ∑(СA—СА)2, что изображено на рис. 13,6 в виде линий равной суммы квадратов отклонений. По методу Гаусса — Зейделя поиск констант ведут следующим образом. Приблизительно оценивают одну из констант, например 0ь и описанным выше способом находят вторую константу 02. Затем фиксируют последнюю величину и отыскивают тем же способом другую константу 01, дающую минимальную остаточную сумму квадратов. Эти операции повторяют до тех пор, пока не будут найдены оптимальные значения констант, дающие глобальный минимум ∑(СА—СА)2, что изображено на рис. 13,6 в виде ступенчатой линии. При усложнении уравнений и наличии -большого числа констант описанный метод требует большой вычислительной работы. Поэтому вместо него используют другие, более ускоренные методы поиска оптимальных значений констант (методы градиентов, нелинейных оценок и др.). При обработке опытов по нелинейному МНК требуется большая вычислительная работа. Это объясняется тем, что кинетические уравнения чаще всего неразрешимы в явном виде в отношении Сг или Х\.Кроме того, многие уравнения интегрируются лишь численными методами, а кинетические модели часто содержат системы взаимосвязанных дифференциальных и алгебраических уравнений. Поэтому обработку опытов ведут на цифровых ЭВМ’ по специальным стандартным программам. Обязанности химика-технолога при этом состоят обычно в проведении эксперимента, выдвижении гипотез о механизме реакций и построении кинетических моделей, а также в анализе результатов
Рис. 15. Визуальный способ проверки адекватности уравнений (кривые) экспериментальным данным (точки). вычислений на ЭВМ. Сами же вычисления, выбор программ для них и т. д. проводятся программистами и операторами на ЭВМ. После нахождения оптимальных значений констант необходимо убедиться в адекватности описания эксперимента полученным кинетическим уравнениям (моделям). Для предварительной оценки адекватности существуют визуальные методы. Такт для линеаризованных форм уравнений, имеющих не более двух неизвестных констант, т. е. у = b1X1или у—можно вычислить из экспериментальных данных значения у и хдля каждой экспериментальной точки и отложить их на графике в соответствующих координатах (рис. 14). Если экспериментальные точки удовлетворительно укладываются напрямую, это делает вероятным, что уравнение адекватно описывает эксперимент. При этом отрезок, отсекаемый на оси ординат, соответствует константе Ь0, а тангенс угла наклона прямой — константе b. При наличии одной неизвестной константы прямая экстраполируется в начало координат. Следовательно, этим путем можно предварительно оценить адекватность уравнения еще до нахождения констант, которые затем определяют описанными ранее способами (а не по отрезкам или по тангенсам угла наклона «на глаз» проведенных прямых). Другой визуальный метод оценки адекватности применяют при обработке опытов по нелинейным уравнениям и для сложных реакций. Он состоит в сопоставлении рассчитанных по кинетическому уравнению (кривые) и экспериментальных (точки) концентраций или выходов веществ (рис. 15) и в сопоставлении их с «коридором» ошибок. Близкое их соответствие и отсутствие систематических отклонений также позволяют оценить адекватность модели опыту. Именно такой способ применяют при обработке опытов на аналоговых ЭВМ, которые не позво- ляют, однако, точно оценить константы, их доверительные интервалы и адекватность модели. Окончательная проверка адекватности должна проводиться методами математической статистики. Один из распространенных способов состоит в сравнительной оценке дисперсий в опытах с варьированием параметров и в параллельных опытах. В последнем случае находят дисперсию воспроизводимости s2cили s2x,о которой уже говорилось раньше. Однако при расчетах по функциям у требуется знать дисперсию' воспроизводимости в этой функции. Для этого функцию у рассчитывают для параллельных опытов и обычным образом находят
(другая возможность состоит в дифференцировании функции у и нахождении ∆у по ∆x или∆С при средних значениях варьируемых параметров). С другой стороны, при обработке эксперимента всегда рассчитывают суммы квадратов отклонений ∑(yi—yi)2или ∑(Сi—Ci)2между экспериментальными и вычисленными значениями функций у или концентраций Сi. Из них находят так называемую дисперсию адекватности
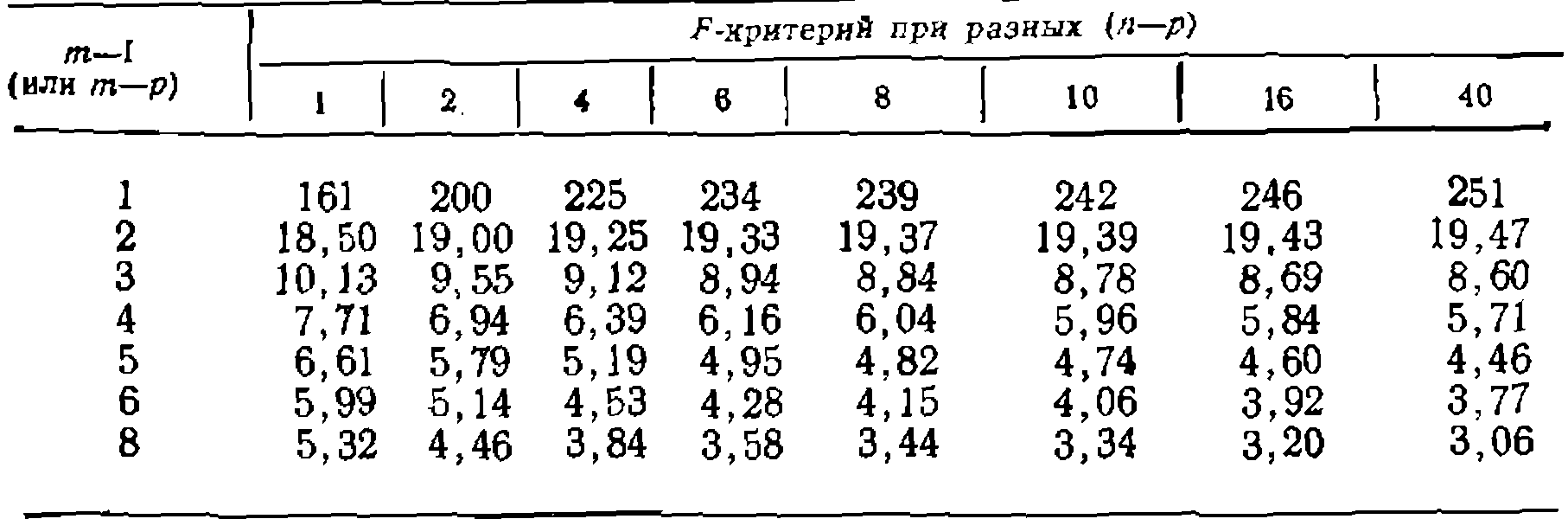
где п — число опытов (экспериментальных точек) с варьируемыми параметрами, р — число определяемых из них констант уравнений, а (п—р) — число степеней свободы при нахождении констант. Если теперь разделить дисперсию адекватности на уже известную дисперсию воспроизводимости, то получим опытное значение критерия Фишера:
При адекватности модели с экспериментом опытное значение этого критерия должно быть меньше табличного. Табулированные значения критерия Фишера зависят от числа степеней свободы в опытах с варьированием параметров (п— —р), от числа опытов на -воспроизводимость (m—1 илиm—р), а также от так называемого уровня значимости, под которым понимают вероятность отклонения эксперимента от модели. Для химических и химико-технологических исследований считается достаточным уровень значимости 0,05 (или доверительная вероятность 95%), для которого значения критерия Фишера приведены в табл. 8. ' Если опытное значение критерия Фишера больше табличного, то предложенная модель неадекватна экспери
Таблица 8. F-критерий для уровня значимости 0,05
менту и должна быть отвергнута. То же самое можно установить без расчета Однако первая же кинетическая модель, не противоречащая опытным данным, еще не может считаться наиболее вероятной или достоверной. Важно проверить все возможные механизмы и построенные из них кинетические уравнения. При этом может оказаться, что опыты удовлетворительно описываются двумя или более моделями. Для выбора между ними проводят дискриминацию моделей, ставя дополнительные опыты в такой области значений параметров процесса, в которой можно ожидать наибольшего расхождения между разными гипотезами. К сожалению, этими дополнительными процедурами нередко пренебрегают, что привело к появлению в литературе сомнительных моделей реальных химических процессов. В результате изложенной обработки опытов обычно остается единственная кинетическая модель, адекватно описывающая экспериментальные данные (иногда несколько кинетически неразличимых моделей). В заключение для нее рассчитывают дисперсии и доверительные интервалы найденных констант (параметров) уравнений. Для линейных моделей основная информация об этом содержится в матрице ошибок торой на дисперсию адекватности дает так называемую ковариационную матрицу «обой симметричную матрицу с размерностью рХр'.
Выделенные жирным шрифтом диагональные элементы связаны •с дисперсией соответствующего параметра соотношением
Когда поиск констант ведут с помощью нелинейного МНК, то дисперсии параметров находят, основываясь на разложении функции в ряд Тейлора. При этом члены матрицы X, имеющей разность пХр, находят из значений частных производных концентраций, степеней конверсии или выходов по каждому из параметров для каждой экспериментальной точки. В действительности значения хц находят по разностям рассчитанных значений концентраций или выходов при небольшом изменении данного параметра по отношению к ранее найденной его величине, т. е.
Из этой матрицы X обычным путем вычисляют матрицу ошибок и затем ковариационную матрицу
где. t — так называемый критерии Стьюдента. Его значения зависят от числа степеней свободы в опытах с варьированием параметров и уровня значимости. Значения критерия Стьюдента для уровня значимости 0,05 таковы:
Во всех случаях квадратный корень из дисперсии параметра дает среднюю квадратичную ошибку, а доверительный интервал параметра вычисляют по формулам
•S 0.j vQii*
С учетом найденного доверительного интервала из значения параметра (константы) исключают лишние значащие цифры н приводят его с указанием доверительного интервала. Так, если была иайдена константа вал
Рис. 16. Доверительные эллинсы двух констант кинетического уравнения при* отсутствии корреляции (i) и при закор- релированности параметров (2).
этом случае полагается провести пересчет параметров по измененной модели. При наличии в кинетическое» уравнении только одной константы доверительный интервал надежно указывает, что истинная ее величина с 95%-й вероятностью находится в пределах этого интервала. При двух или более параметрах существует доверительная область параметров* представляющая собой эллипс или эллипсоид в р-мерном пространстве, центром которого являются найденные значения констант В отсутствие так называемой закоррелированности параметров доверительный эллипс (эллипсоид) имеет оси, параллельные осям параметров (рис. 16, i), причем проекции его на оси координат равны удвоенному доверительному интервалу, вычисленному из соотношения (II-65). При закоррелированности параметров доверительный эллипс- (эллипсоид) оказывается более вытянутым и наклоненным к: осям координат (рис. 16,2). В этом случае само понятие доверительного интервала каждой из констант оказывается условным. Если считать его равным полупроекции эллипса (эллипсоида) на оси координат, то он будет включать большую область значений констант, выходящих за пределы 95%-й вероятности* В меньшей степени это относится к доверительному интервалу* спроектированному на оси параметров на рис, 16,2,и соответствующего тому, который рассчитывают по формулам (II-65). Однако он исключает часть доверительного эллипса (эллипсоида) и в то же время включает области (на рисунке заштрихованы) за его пределами. Поэтому при закоррелированности параметров, строго говоря, доверительный интервал теряет какой- либо смысл, хотя его часто вычисляют и приводят. Наилучшим решением является построение доверительного эллипса (эллипсоида) или указание его основных характеристик (соотношение главных осей, угол наклона). Другая возможность состоит в вычислении доверительного» интервала, ио с указанием коэффициентов закоррелированности параметров. Эти коэффициенты находят по недиагональным элементам (ковариациям) ковариационной матрицы
коэффициент закоррелированности параметров может меняться от 0 до 1, что соответствует нулевой и полной закоррелированности. Иногда он бывает очень большим, например, при нахождении предэкспоненты и энергии активации по уравнению Аррениуса. Закоррелированность параметров — свойство данной кинетической модели или уравнения, но иногда она появляется из- за неверной постановки опытов. Например, если для уравнения то степень корреляции констант существенно увеличивается, и в пределепри
Отметим, что при большом числе параметров кинетической модели и их закоррелированности друг с другом возрастают трудности в точном нахождении констант и появляется опасность в «подгонке» результатов под разные модели. Поэтому важное значение имеет независимое нахождение отдельных констант или их соотношений кинетическими или иными методами^ для данного ключевого вещества, i—число этих веществ, а п— число опытов с варьированием параметров. После этого дисперсию адекватности и критерий Фишера находят обычным образом, но для каждого из ключевых веществ. Кроме линейного и нелинейного МНК существуют два? способа обработки эксперимента: интегральный и дифференциальный. Первый применяют при постановке опытов в периодических условиях или в реакторе идеального вытеснения, когда- — оценка дисперсии воспроизводимости
Обработка кинетических даицых для сложных реакций имеет некоторые особенности. В этом случае полная модель состоит из уравнений скорости для каждого ключевого вещества и уравнений баланса с р неизвестными параметрами. Иногда эту модель удается упростить и уменьшить число неизвестных констант путем предварительного определения соотношений констант по количественным закономерностям в составе образующихся продуктов. Тем не менее модель обычно coctohi из системы взаимозависимых уравнений, часть которых содержит одни и те же неизвестные константы и концентрации веществ. Вследствие этого поиск параметров ведут по модели в целом, но для нахождения единственной оптимальной величины каждой константы необходимо минимизировать взвешенную сумму квадпатов отклонений лля всех ключевых вешеств. ' т. е. шначале необходимо подставить выражения скорости в уравнения соответствующих реакторов и решить интегралы. При втором способе обработку ведут прямо по дифференциальным кинетическим уравнениям, находя значения скоростей из опытов в безградиентных условиях или дифференцированием кинетических кривых. Ниже эти способы рассматриваются в применении ко все более сложным кинетическим уравнениям и моделям. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|



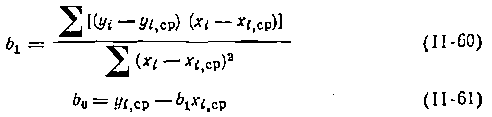




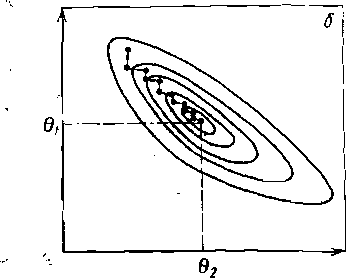

 Рис. 14. Линеаризация экспериментальных данных для кинетических уравнений с одной (/) я двумя \(2) неизвестными константами при обработке опытов с помощью линейного МНК.
Рис. 14. Линеаризация экспериментальных данных для кинетических уравнений с одной (/) я двумя \(2) неизвестными константами при обработке опытов с помощью линейного МНК.



 и
и  по несоответствию опытных данных расчетным прямым на рис. 14 или кривым на рис. 15. Неадекватность уравнений сразу выявляется и в тех случаях, когда найденные константы скоростей, константы равновесия или адсорбционные коэффициенты имеют отрицательную величину (если их доверительный интервал не включает нуля или положительных значений), когда их величина противоречит физическому смыслу или достоверным литературным данным, и т, д. Во всех этих случаях приходится уточнить первоначальную гипотезу о механизме реакций или выдвинуть другую, построить новую кинетическую модель и повторить обработку опытов, пока не будет достигнута адекватность уравнений с экспериментом.
по несоответствию опытных данных расчетным прямым на рис. 14 или кривым на рис. 15. Неадекватность уравнений сразу выявляется и в тех случаях, когда найденные константы скоростей, константы равновесия или адсорбционные коэффициенты имеют отрицательную величину (если их доверительный интервал не включает нуля или положительных значений), когда их величина противоречит физическому смыслу или достоверным литературным данным, и т, д. Во всех этих случаях приходится уточнить первоначальную гипотезу о механизме реакций или выдвинуть другую, построить новую кинетическую модель и повторить обработку опытов, пока не будет достигнута адекватность уравнений с экспериментом. , умножение ко
, умножение ко Последняя представляет
Последняя представляет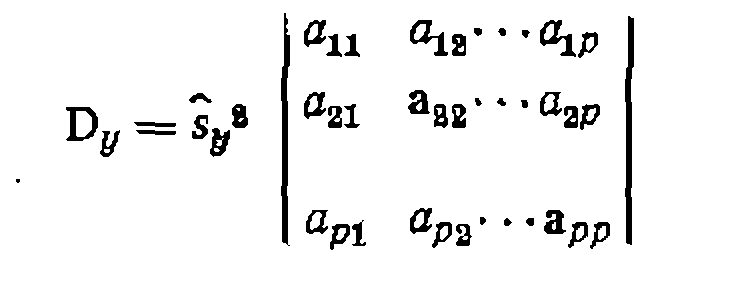
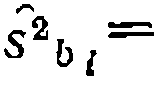
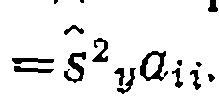
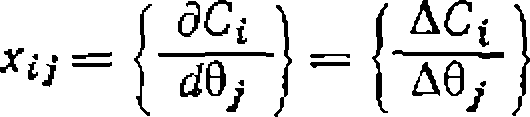
 или
или . Ее диагональные элементы, как и раньше, равны дисперсии соответствующего параметра, т. е.
. Ее диагональные элементы, как и раньше, равны дисперсии соответствующего параметра, т. е.  или
или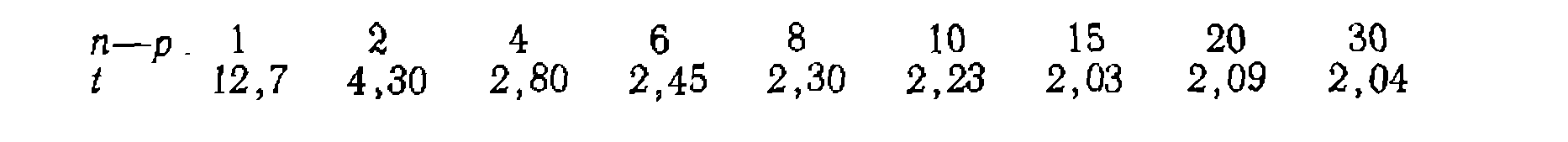
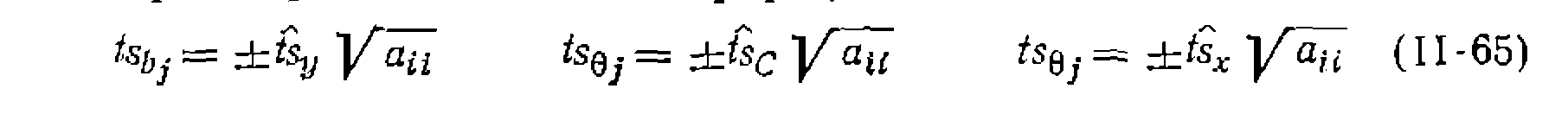
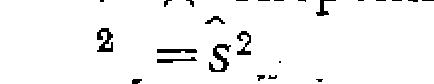
 и ее доверительный интер
и ее доверительный интер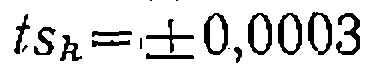 , то записывают решение в виде
, то записывают решение в виде 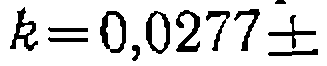
 Когда доверительный интервал получился больше самого параметра, последний принимают равным нулю. Это равноценно отсутствию данно-го члена кинетической модели, и в
Когда доверительный интервал получился больше самого параметра, последний принимают равным нулю. Это равноценно отсутствию данно-го члена кинетической модели, и в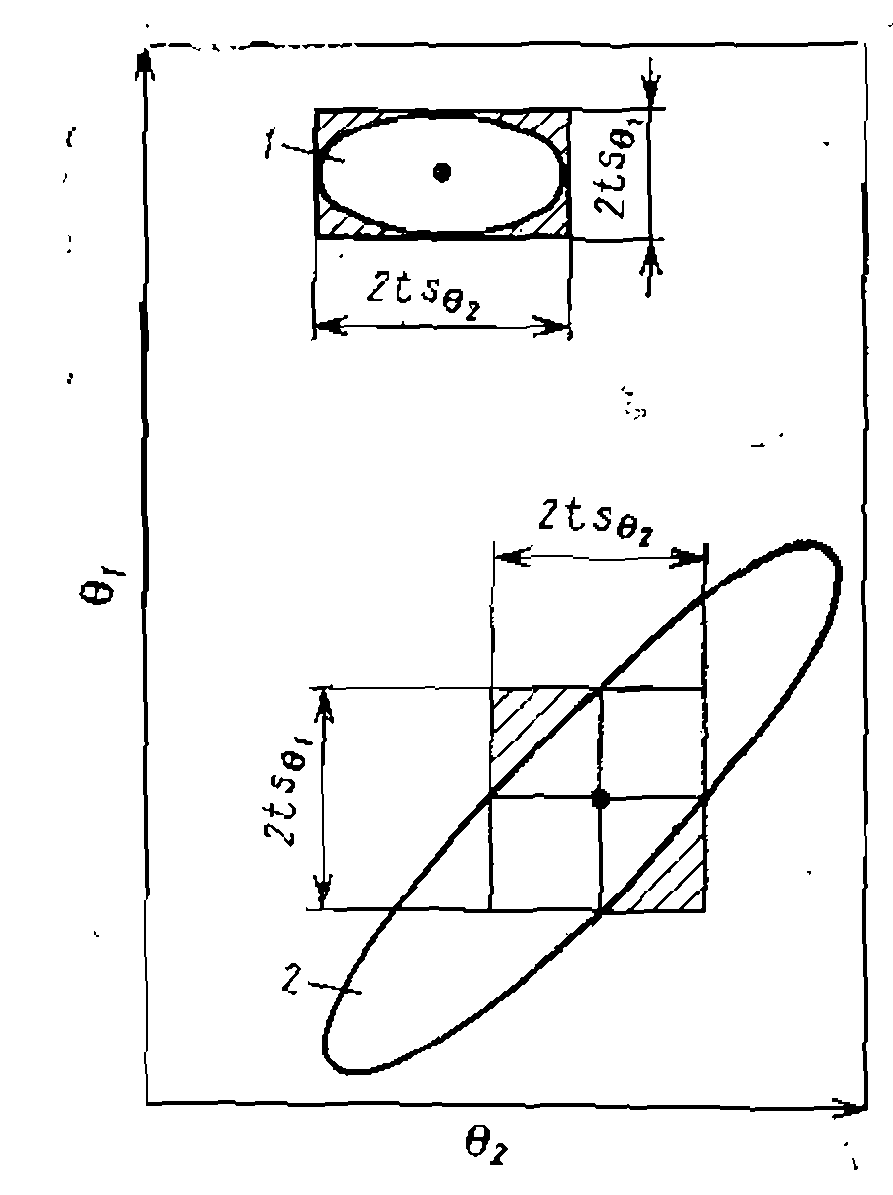
 или
или  (рис. 16). При этом 'имеется 95%-я вероятность, что истинные значения каждой из констант находятся т$. пределах, ограниченных этим эллипсом (эллипсоидом).
(рис. 16). При этом 'имеется 95%-я вероятность, что истинные значения каждой из констант находятся т$. пределах, ограниченных этим эллипсом (эллипсоидом).
 опыты ставились при
опыты ставились при  или при
или при  „
„ или при
или при  можно найти только
можно найти только или
или  . Именно поэтому одно из важных требований к эксперименту— возможно более широкое варьирование параметров процесса.
. Именно поэтому одно из важных требований к эксперименту— возможно более широкое варьирование параметров процесса.