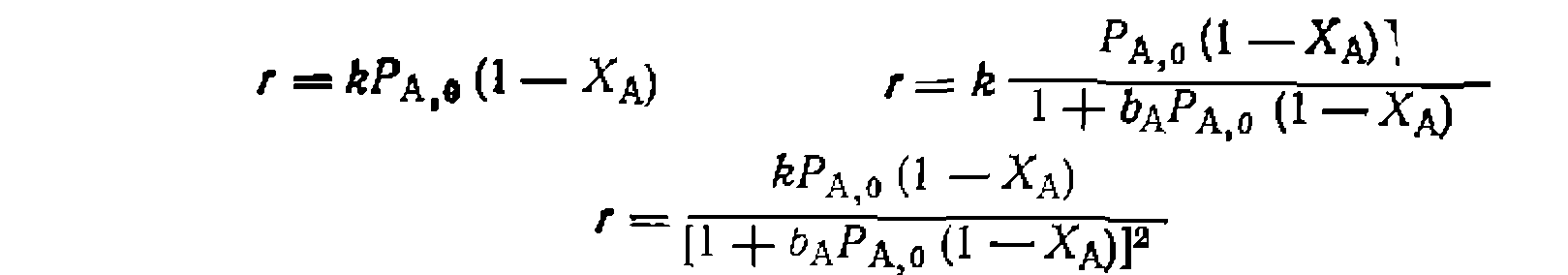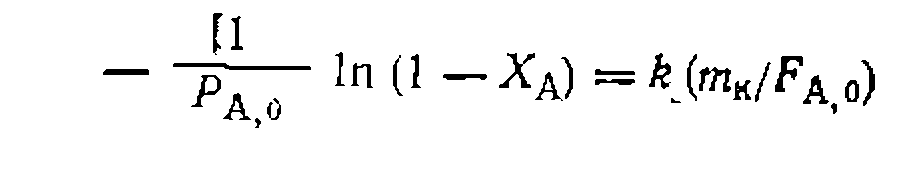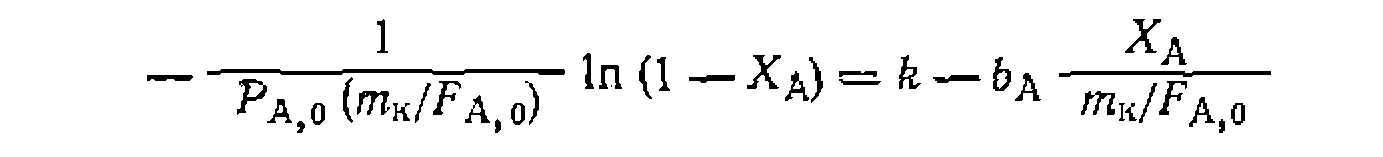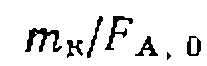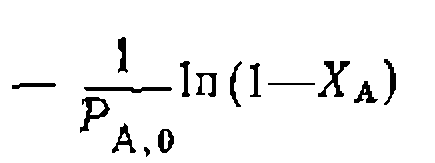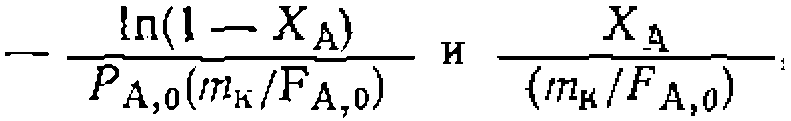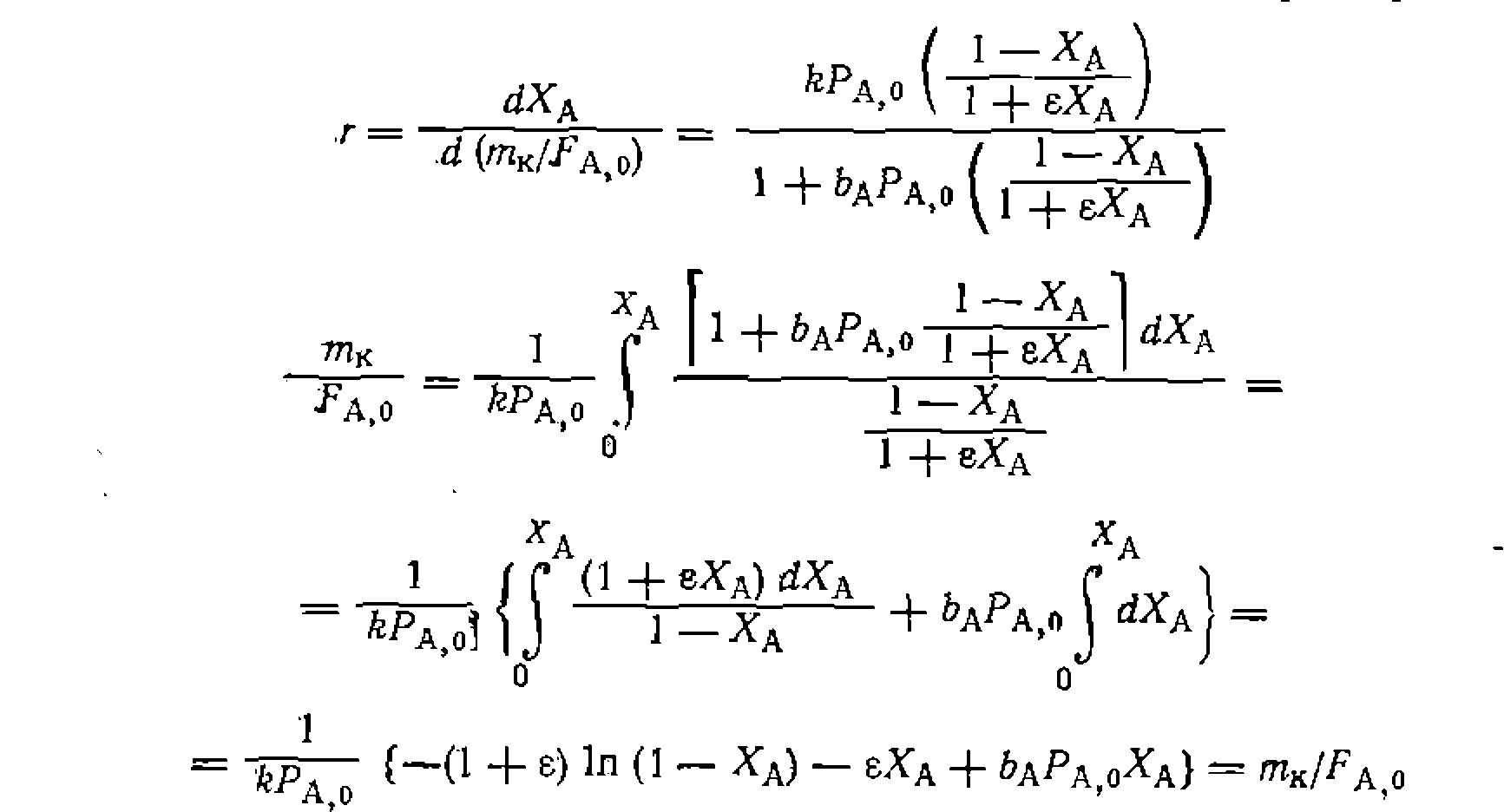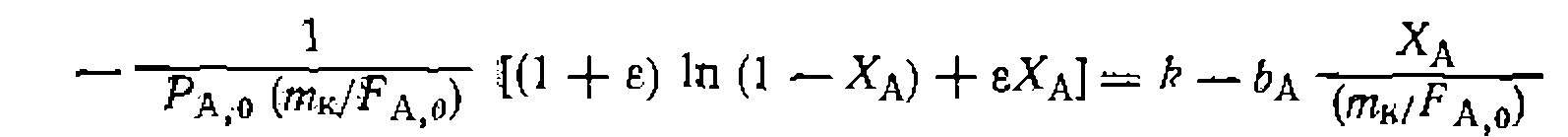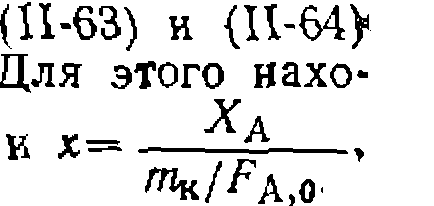|
|
При поиске констант нелинейным МНК было нолучено
н кинетическое уравнение:
и получаем:
При средних значениях Са=1,22, Са = 0,65 и С'а= —1,65 имеем':
Отсюда вычисляем дисперсию воспроизводимости
и опытное значение критерия Фишера
что меньше его табличного значения . . Находим дисперсию, среднюю квадратичную ошибку и доверительный интервал найденной константы уравнения:
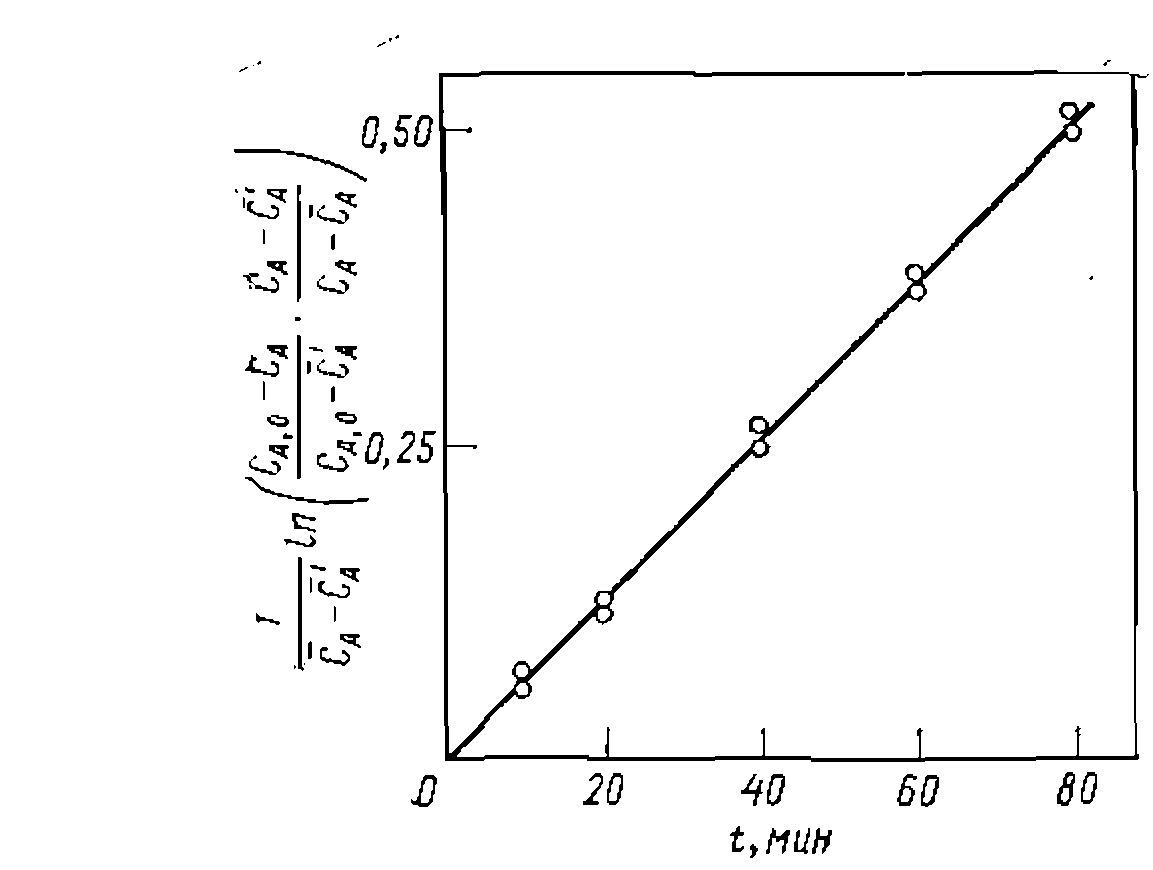
ИНТЕГРАЛЬНЫЙ МЕТОД ОБРАБОТКИ ОПЫТОВ ДЛЯ ПРОСТЫХ И ОБРАТИМЫХ РЕАКЦИЙ ПО УРАВНЕНИЯМ С ДВУМЯ И БОЛЕЕ НЕИЗВЕСТНЫМИ ПАРАМЕТРАМИ Как мы видели выше, такие кинетические уравнения часто встречаются для простых и обратимых реакций со 'Сравнимыми скоростями отдельных элементарных стадий и (или) для таких реакций, при которых реагенты либо катализаторы находятся в разных формах. При этом многочлен со своими константами может находиться в числителе кинетического уравнения (обратимые реакции с неизвестной константой равновесия и др.) или Рис. 19.. Линеаризация опытов при интегральной обработке кинетических данных для обратимой реакции второго порядка, изучаемой в периодических условиях. в знаменателе (члены, определяющие расходование промежуточной частицы, или функции закомплексованности). К этому же типу принадлежат кинетические модели с единственным кинетическим уравнением и со аиями баланса по реагентам, )ости во избежание его чрез- )тся интегральной обработке ши, содержащими многочлен 1гко интегрируются, и их ин- j линейныймногочлен у = араметры ди только двух констант — зость способом графической обных уравненийпокажем ере, когда
сложными алгебраическими уравнениями бала которые не вводят в уравнение скорости во из мерного усложнения. Сравнительно просто подвергаются интегр реакции с кинетическими уравнениями, содерн в знаменателе. Такие уравнения легко интегр тегральная форма преобразуется в линейный \—bo-\-b\XiJrb2X2-\-...) по которому параметры дить линейным МНК, а при наличии только предварительно проверять адекватность спосс линеаризации в координатах
Чтобы получить линейную форму уравнения типа
нужно преобразовать полученное выражение таким образом, чтобы одна из констант находилась в свободном виде, а в левую часть перенести члены, не содержащие констант. Для этого делим обе части уравнения на t и умножаем на или
Откладывая против можно предвари тельно проверить соответствие уравнения опыту и приближенно оценить значения констант, которые затем вычисляют обычным образом. В этой и подобных ей формах линейных уравнений с двумя и более параметрами не только у, но и х являются функциями переменных, причем каждая из них содержит ошибку. Такие уравнения называют корреляционными, и их параметры обычно определяются с более значительной погрешностью. Это* усугубляется закоррелированностью констант, что делает предпочтительным применение нелинейного МНК при обработке опытов. Пример. Необратимую гетероген но-каталитическую реакцию
изучали в газовой фазе в реакторе, близком к модели идеального вытеснения, нри 7=const, избытке водорода и общем давлении 1,00 МПа. Были по* лучены такие результаты:
Требуется обосновать кинетическое уравнепне, найти его константы, их доверительные интервалы и коэффициенты эакоррелировапности констант, а также построить доверительный эллипсоид, используя липейный и иелинейг; ный МНК. Среднее отклонение при четырех параллельных опытах составило#
Из-за избытка водорода множитель Ру можно ввести в константу , а чле*- нами парафина и водорода на поверхности катализатора {иногда это же относится и к члену ЬаРа)- При предварительной оценке гипотез пренебрегаем небольшим изменением объема во время реакции, проверяя три наиболее простые возможности:
Первое из уравнений дает прн решении интеграла
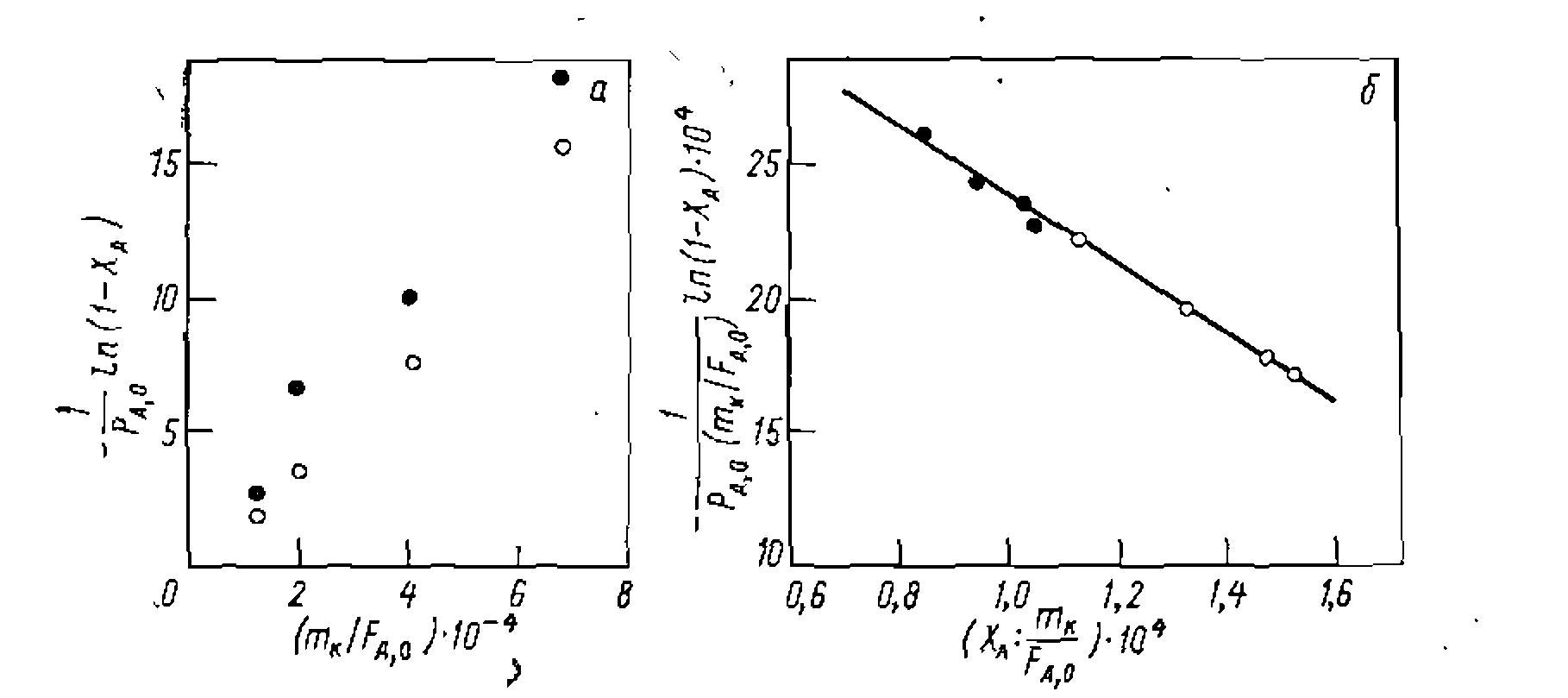
Рис. 20. Линеаризация опытов нрн интегральной обработке кинетических данных для гетерогенно-каталитической реакции по уравнениям нервого норядка (о) и с двумя нараметрами ,(б). (рис. 20, о) ноказывает неудовлетворительные результаты. Для второго варианта интегрирование дает линейное уравнение
Расчет функции
и ее графическое изображение .против
,отклады Рассчитываем из опытов функции вая их значения на графике (рис. 20,6). Видно, что онытные данные удовлетворительно уложились на одну прямую, нз чего можно сделать предварительный вывод об адекватности этого уравнения оныту. Для более точной оценки констант уравнения учтем изменение объема смеси во время реакции:

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
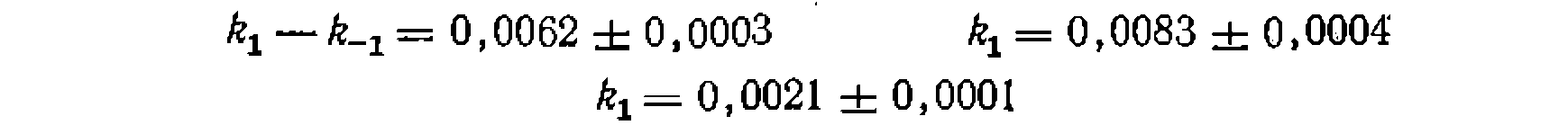
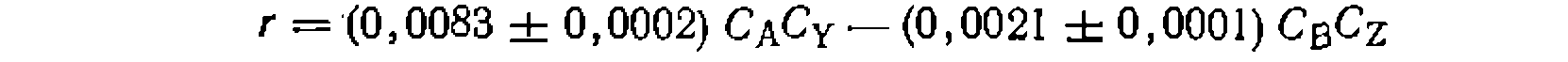
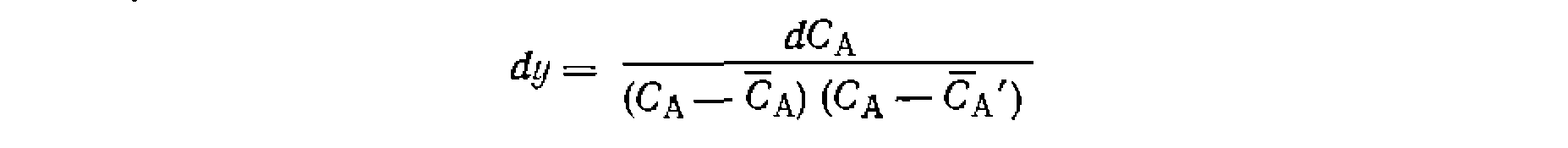
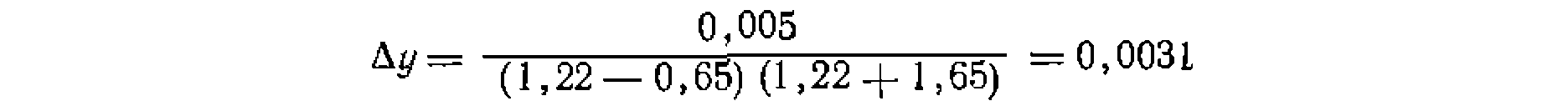
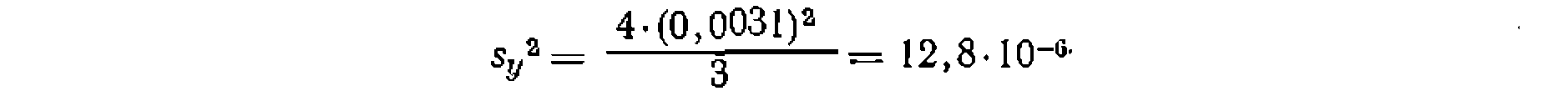
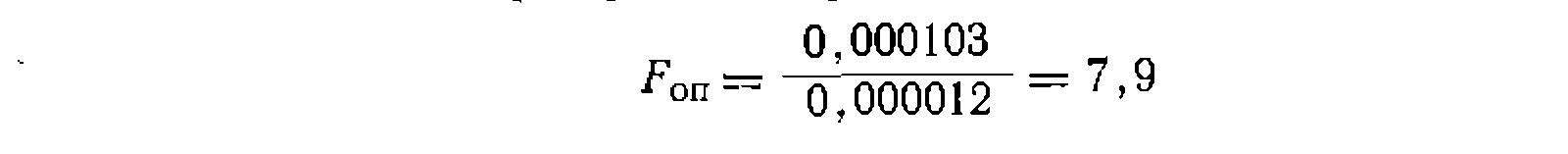
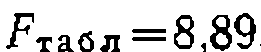
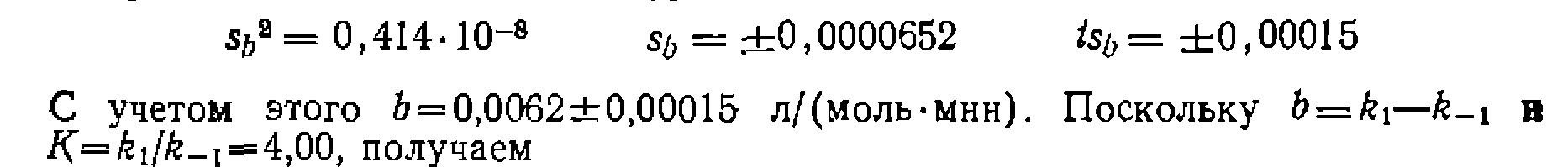

 можно нахо
можно нахо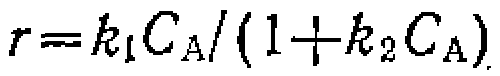
 ! Ввиду многообразия типов подобных ур; эту процедуру лишь на одном примере, когда В периодических условиях получим:
! Ввиду многообразия типов подобных ур; эту процедуру лишь на одном примере, когда В периодических условиях получим: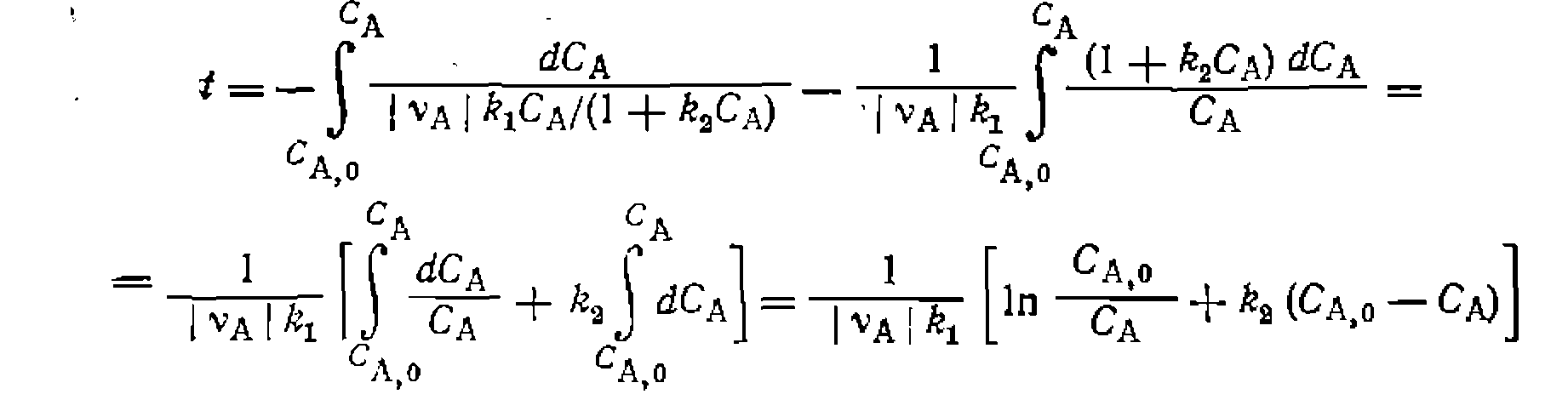
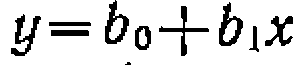 ,
,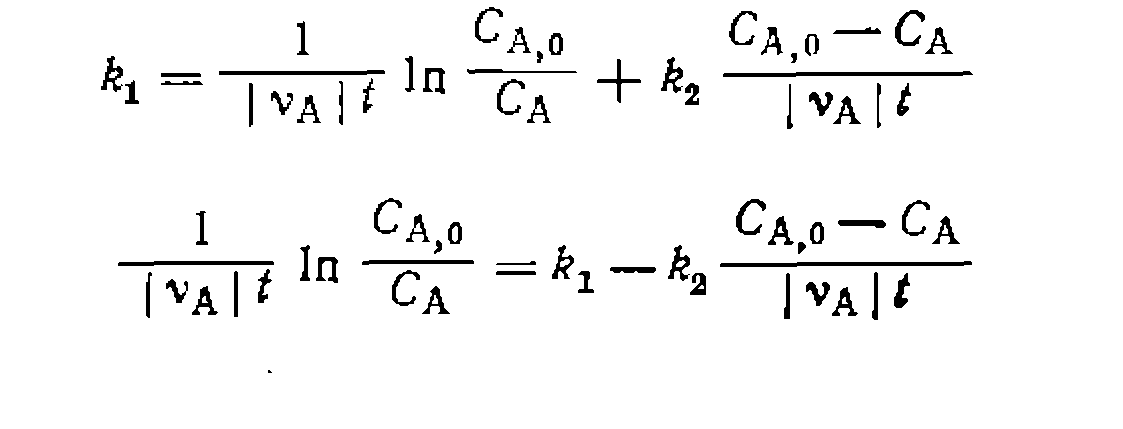
 . В результате получаем:
. В результате получаем: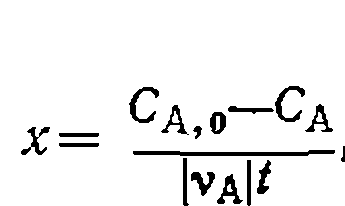
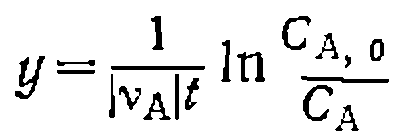
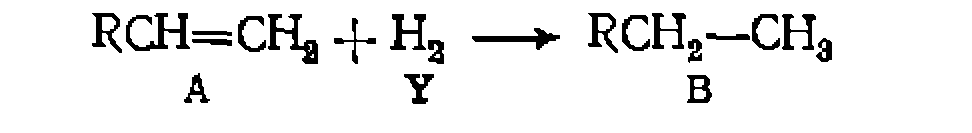

 , дисперсия воспроизводимости
, дисперсия воспроизводимости  Из литературных данпых по кинетике гидрирования олефииов известно, что возможен ряд механизмов реакции и кинетических уравнений следующего общего типа:
Из литературных данпых по кинетике гидрирования олефииов известно, что возможен ряд механизмов реакции и кинетических уравнений следующего общего типа: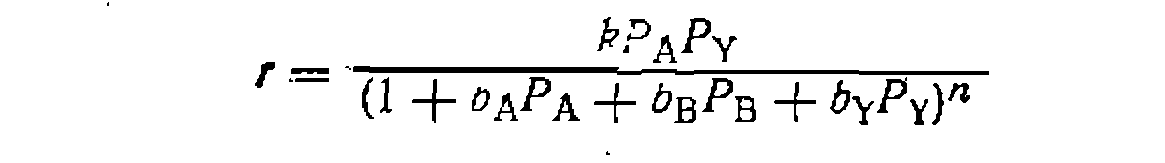
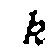
 и
и  , видимо, можно пренебречь вследствие слабой адсорбции
, видимо, можно пренебречь вследствие слабой адсорбции