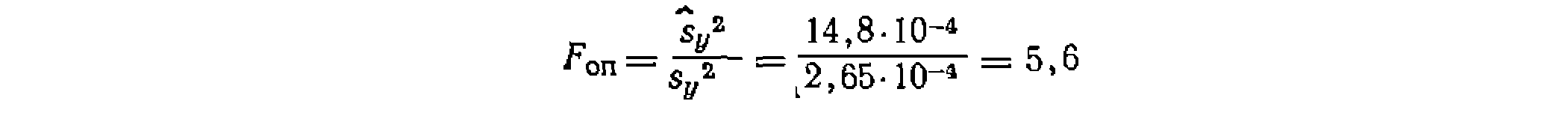|
|
ИНТЕГРАЛЬНЫЙ МЕТОД ОБРАБОТКИ ОПЫТОВ ПО УРАВНЕНИЯМ С ОДНИМ НЕИЗВЕСТНЫМ ПАРАМЕТРОМК указанному типу относятся необратимые простые реакции, •описываемые кинетическим уравнением , а также об ратимые реакции с аналогичными уравнениями при известной константе равновесия. Необратимые простые реакции в периодических условиях. . Для них кинетическое уравнение, построенное из механизма, можно преобразовать как функцию концентрации основного реагента А. Так как объем обычно остается постоянным, то концентрацию второго реагента Y находят из баланса
и тогда кинетическое уравнение будет таким:
В другом, часто применяемом выражении, используют переменную х, равную полноте реакции на 1 л реакционного раствора (т. е.
а уравнение скорости имеет вид: В другом, часто применяемом выражении, используют переменную х, равную полноте реакции на 1 л реакционного раствора (т. е. . Тогда, обозначив начальные концентрации реагентов А и Y через а и Ь. получим их текушие коннентоации-
Решения уравнений (II-67) и (II-68) для наиболее часто встречающихся порядков реакций приведены в табл. 9. Для всех приведенных уравнении предварительная проверка их соответствия опыту достигается путем линеаризации. Для этого левые части интегральных выражений откладывают против времени, получая прямую, выходящую из начала координат и имеющую тангенс угла наклона, равный константе скорости реакции. Дальнейшую обработку опытов ведут или с помощью линейного МНК по уравнению w , или с помощью" нелинейного МНК, для которого используют полученную при линеаризации предварительную оценку константы. Решения уравнений (II-67) и (II-68) для наиболее часто встречающихся порядков реакций приведены в табл. 9. Для всех приведенных уравнении предварительная проверка их соответствия опыту достигается путем линеаризации. Для этого левые части интегральных выражений откладывают против времени, получая прямую, выходящую из начала координат и имеющую тангенс угла наклона, равный константе скорости реакции. Дальнейшую обработку опытов ведут или с помощью линейного МНК по уравнению w Пример. Жидкофазная реакция изучалась в периодических условиях в гомогенной среде при ностоянной температуре и двух разных начальных концентрациях реагентов. Путем титрова- Таблица 9. Уравнения для интегральной обработки опытов, проведенных в периодических условиях при V = const
ния непревращеиной щелочи и пересчета по балансу ли получены такие данные:
При трех параллельных опытах среднее отклонепие ло новать механизм и кинетическое уравнение реакции, .найти констапту скорости и ее доверительный интервал, используя снособы линейного и нелинейного МНК.
Из литературных данных известно, что для превращений диарнлхлорметанов наиболее вероятен S/Л-механизм. Поэтому предварительно проверяем- соответствие результатов опытовс уравнением 2 из табл. 9 путем их линеаризации в координатах «станты .ведем по простейшему линейпому уравнению ;
’Следовательно, по уравнению (11-62) получим:
‘■Сумма квадратов отклонений равна 133,3258-10“*, откуда дисперсия адек-' ватности составит
Из приведенного в задании среднего отклонения в трех параллельных -опытах ±0,002 моль/л вычисляем среднее отклонение функции , которое при средней величинеСа^О.15 моль/л составит
Из приведенного в задании среднего отклонения в трех параллельных -опытах ±0,002 моль/л вычисляем среднее отклонение функции которое при средней величине Са^О.15 моль/л составит Дисперсия воспроизводимости в этой функции будет равна ;.и, следовательно, критерий Фишера равен ;.и, следовательно, критерий Фишера равен

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
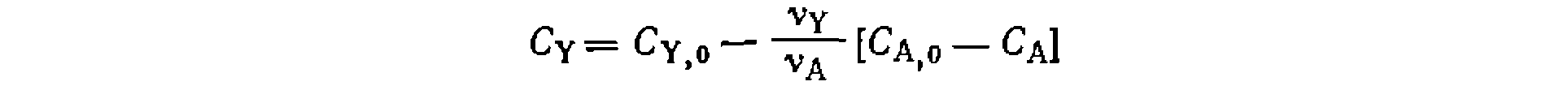
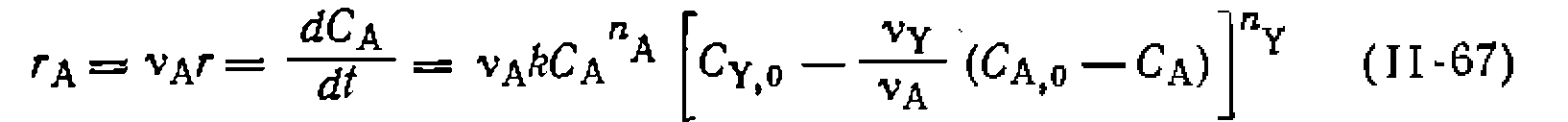
 . Тогда, обозначив начальные концентрации реагентов А иY через а и Ь, получим их текущие концентрации-
. Тогда, обозначив начальные концентрации реагентов А иY через а и Ь, получим их текущие концентрации- а уравнение скорости имеет вид:
а уравнение скорости имеет вид: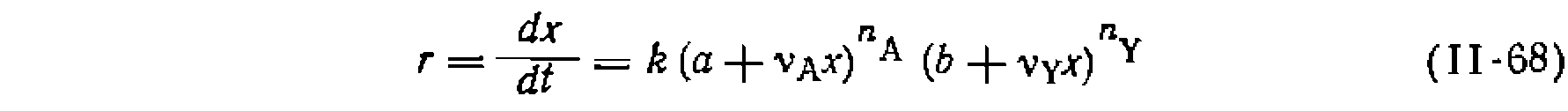
 , или с помощью * нелинейного МНК, для которого используют полученную при линеаризации предварительную оценку константы.
, или с помощью * нелинейного МНК, для которого используют полученную при линеаризации предварительную оценку константы.
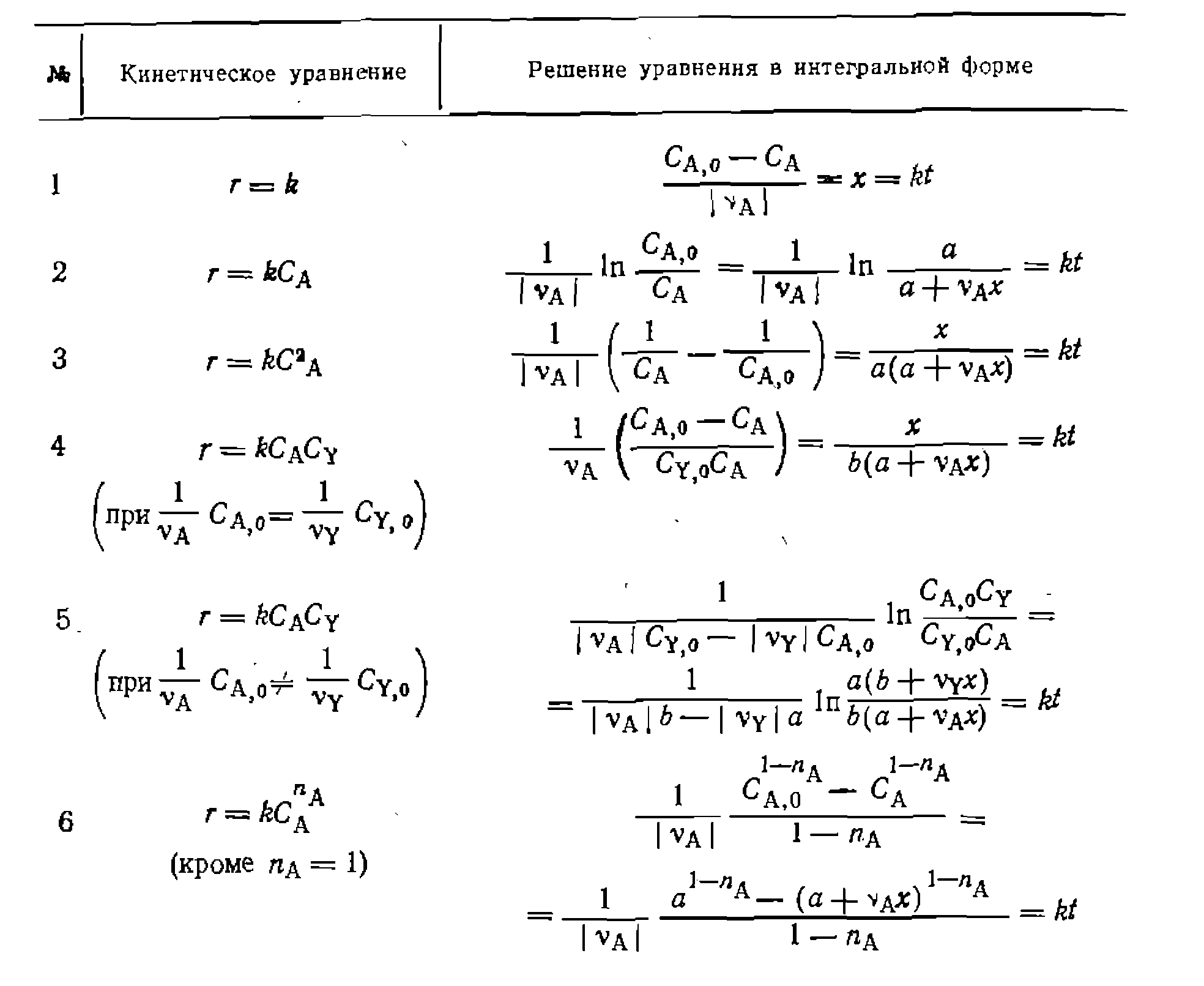
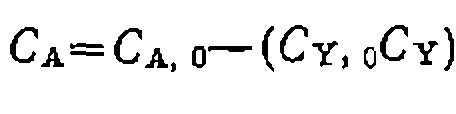

 состави
состави моль/л, а дисперсия воспроизводимости равна
моль/л, а дисперсия воспроизводимости равна 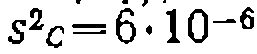 . Обос
. Обос (рнс. 17). Точки удовлетворительно* уложились на прямую, что делает принятую гипотезу вероятной. Поиск кон-
(рнс. 17). Точки удовлетворительно* уложились на прямую, что делает принятую гипотезу вероятной. Поиск кон- , где
, где , для чего вычисляем для каждой точки:
, для чего вычисляем для каждой точки: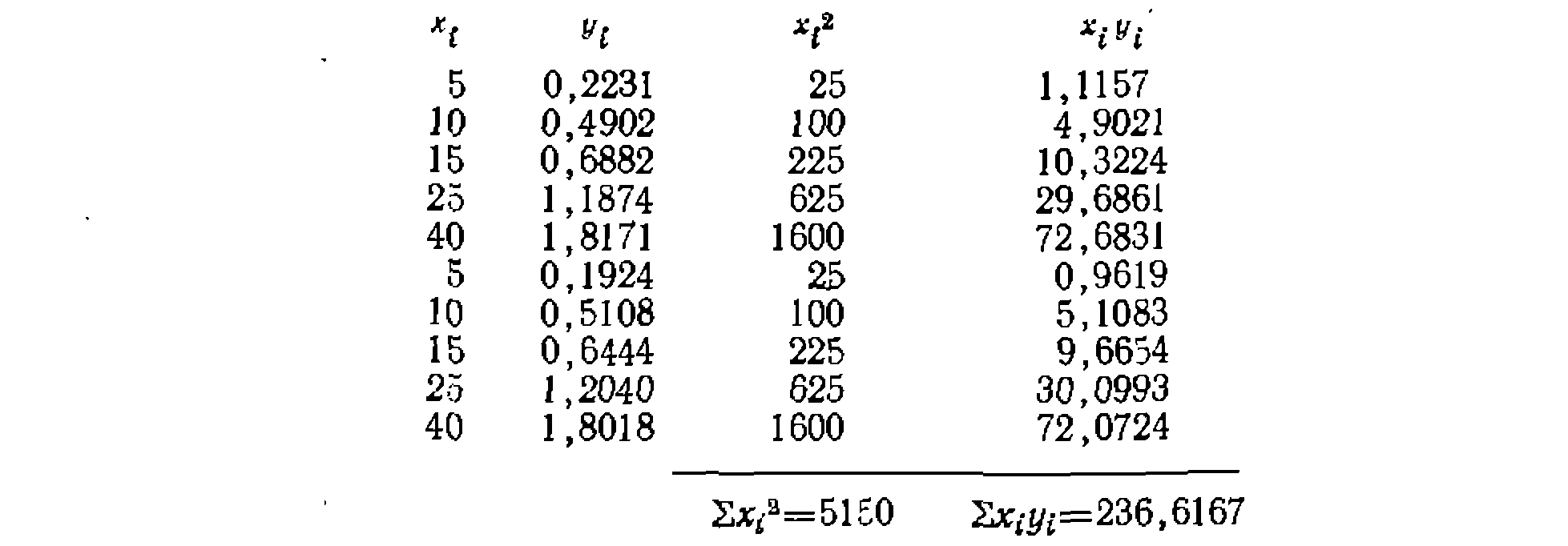
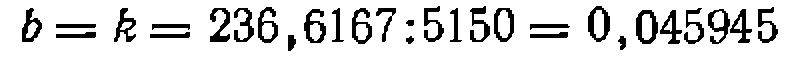

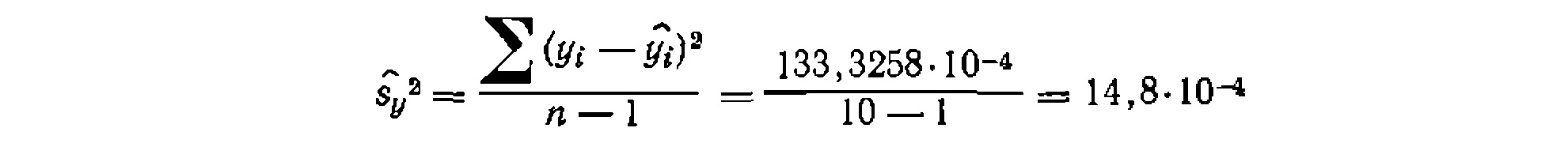
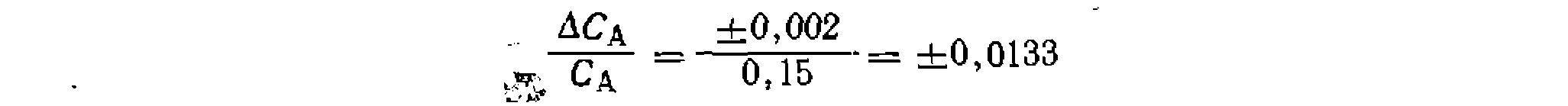
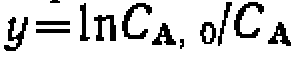 ,
,