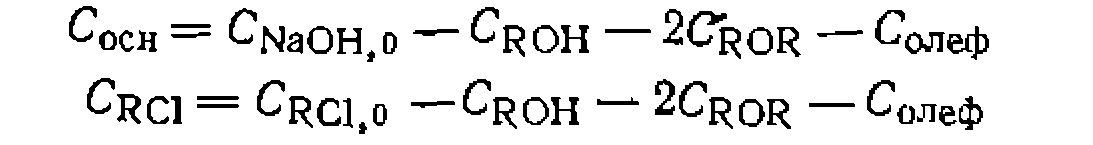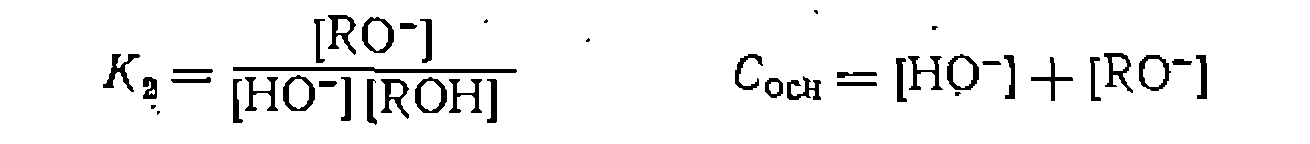|
|
Ризации, которая сильно влияет па результаты расчета..'При подсчете мольной доли продуктов равно 10. Находим среднюю стенеиь олигомеризации*.
«если в продуктах реакции найдены следующие мольные доли олефннов, по* лученных после их вытеснения из алюмииийтриалкилов:
.ших фракций и распределение будет болееузким (кривая 2). Наоборот, при непрерывном увеличении «окажется более широким (кривая 5).
Если соотношение констант порядка тельностей уравнения первой стадии не включают концентрации продуктов; и реагентов других стадий. Другим простым случаем обработки кинетических данных являются последовательно-параллельные* реакции с единственная неизвестная константа может быть найдена по* расходованию второго реагента Y, т. е. по уравнению
Во всех остальных случаях последовательных реакций интегральный способ обработки кинетических данных возможен только на ЭВМ по полной кинетической модели реакции. Пример- этого дан в следующем разделе для более сложных систем реакций. ИНТЕГРАЛЬНЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ БОЛЕЕ СЛОЖНЫХ СИСТЕМ Для сложных систем превращений, как и для рассмотренных. выше параллельных и последовательных реакций, кроме предварительного анализа кинетических кривых для расшифровки схемы превращений и составления кинетической модели важную роль играет количественное изучение соотношения образующихся продуктов. Оно позволяет определить не только путя образования побочных веществ, но и механизм этих реакций и соотношения констант скорости побочных и целевой реакций;
Уравнения соотношения количества образующихся продуктов; записывают в дифференциальном виде:
где При делении скоростей некоторые концентрации и нередко знаменатели уравнений сокращаются, что дает достаточно простые выражения. При наличии определенной гипотезы о механизме и кинетике основной реакции подбирают такие пути н механизм образования побочных веществ, чтобы выведенные уравнения в их интегральной форме адекватно описывали соотношение образующихся продуктов. Пример. При гетерогенно-каталитическом дегидрировании этялбензола в стирол нобочно образуются беизол и толуол. Изучение этого процесса в изотермическом реакторе идеального вытеснения при 576 °С дало такие результаты по степени конверсии этилбензола
"Требуется найти пути и механизм образования побочных веществ, если известно, что кинетика основной реакции
г<онисывается уравнением
-При обработке опытов принимаем, что кинетические уравнения побочных редакций имеют тот же знаменатель. Кроме того, при 576 °С и невысокой степени конверсии можно нренебречь обратимостью реакции дегидрирования. Для образования бензола и толуола возможно несколько путей. По реакции нервого (илн псевдопервого) порядка эти углеводороды могут получаться за счет разложения этилбензола, а также конверсии этилбензола нла стирола избытком водяного пара:
^Реакции второго порядка могут включать гндрогеполиз этилбензола или сти- ,рола водородом, выделяющимся при дегидрировании:
Проверка разных путей образования бензола показала, что для этого подходят только реакции (2) и (7), которые дают следующее дифференциальное уравнение: ,
Ш нем из-за незначительного образования побочных веществ принято, что -Х»б—*ст и Рна = ^о^вв. Интегрирование уравнения приводит к такому решению:
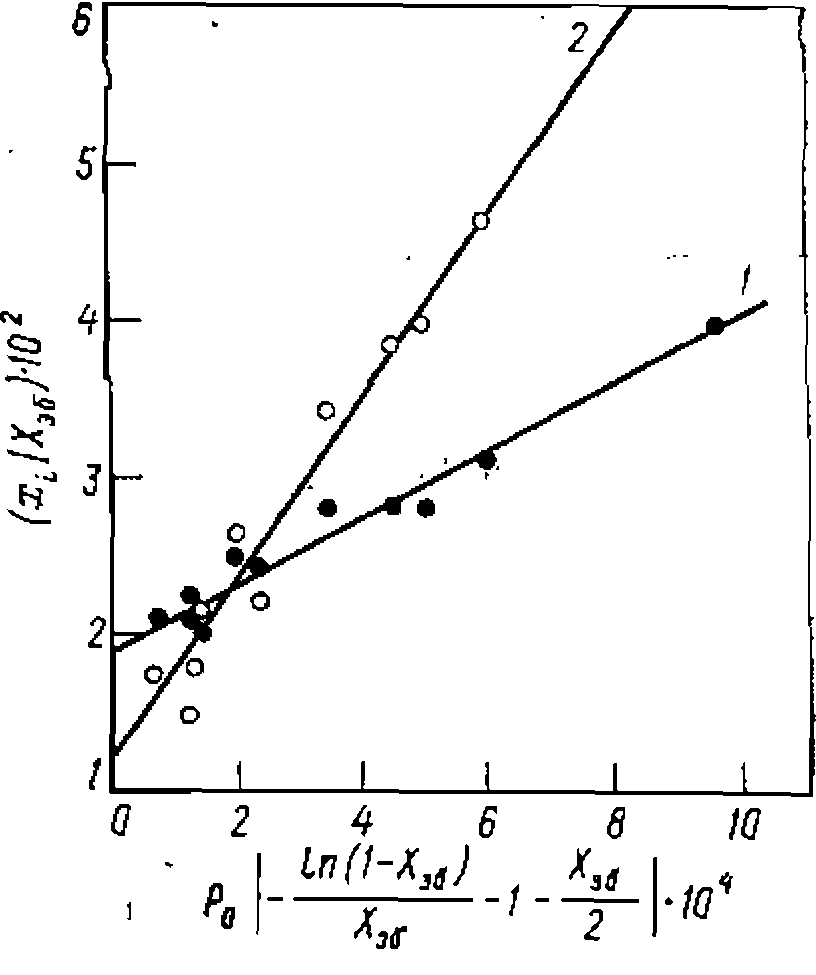
Рис. 26. Линеаризация опытных данных по составу побочных продуктов дегидрирования этилбензола: .
/ — бенэол; 2 — толуол. Представление экспериментальных данных в коордипатах этого уравнения (рис. 26) ноказывает их удовлетворительное соответствие. Прн расчете получено такое соотношение констант:
Для образования толуола лучшим оказалось сочетание реакции (3) и (8), которое прн решении дает то же интегральное выражепие. Линеаризация опытов в координатах этого уравнения (рис. 26) также показала удовлетворительные результаты и следующие соотношения Следовательно, бензол образуется с большей относительной скоростью нз этилбензола, а толуол — из стирола. Полученные данные нетрудно использовать для составления уравнения дифференциальной селективности: •
Обработка кинетических данных для сложных систем параллельных и последовательных реакций, как и для большинства последовательных реакций, осуществляется по их кинетической модели на цифровых ЭВМ. Рассмотрим ее на следующих примерах. Пример. В результате гидролиза хлорпроизводпого при избытке воды в гомогенных условиях образуются спирт, простой эфир и олефин. При изучении этой реакции в периодических условиях были получены такие результаты:
Найти механизмы, кинетическую модель, ее параметры и нх доверительные интервалы, если дисперсия воспроизводимости в четырех параллельных опытах для концентраций спирта, эфира н олефина составила соответственно 4 10-®, 2-1O-0 и Ь10“е. При наиболее вероятных
уравнения констапты равновесия второй реакции, уравнения баланса по разным формам оснований

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 было нринято, что числоi для высших
было нринято, что числоi для высших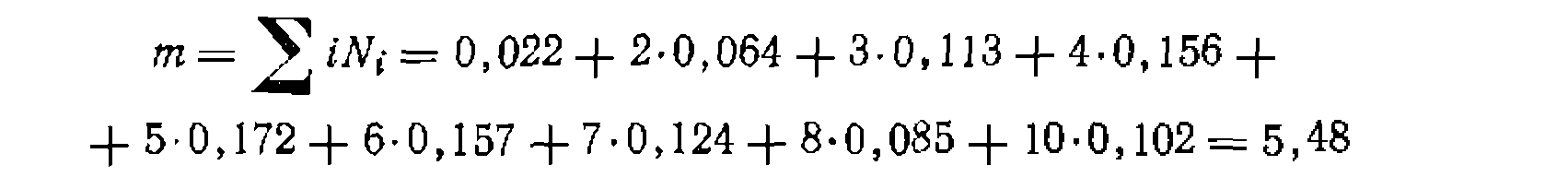

 распределение
распределение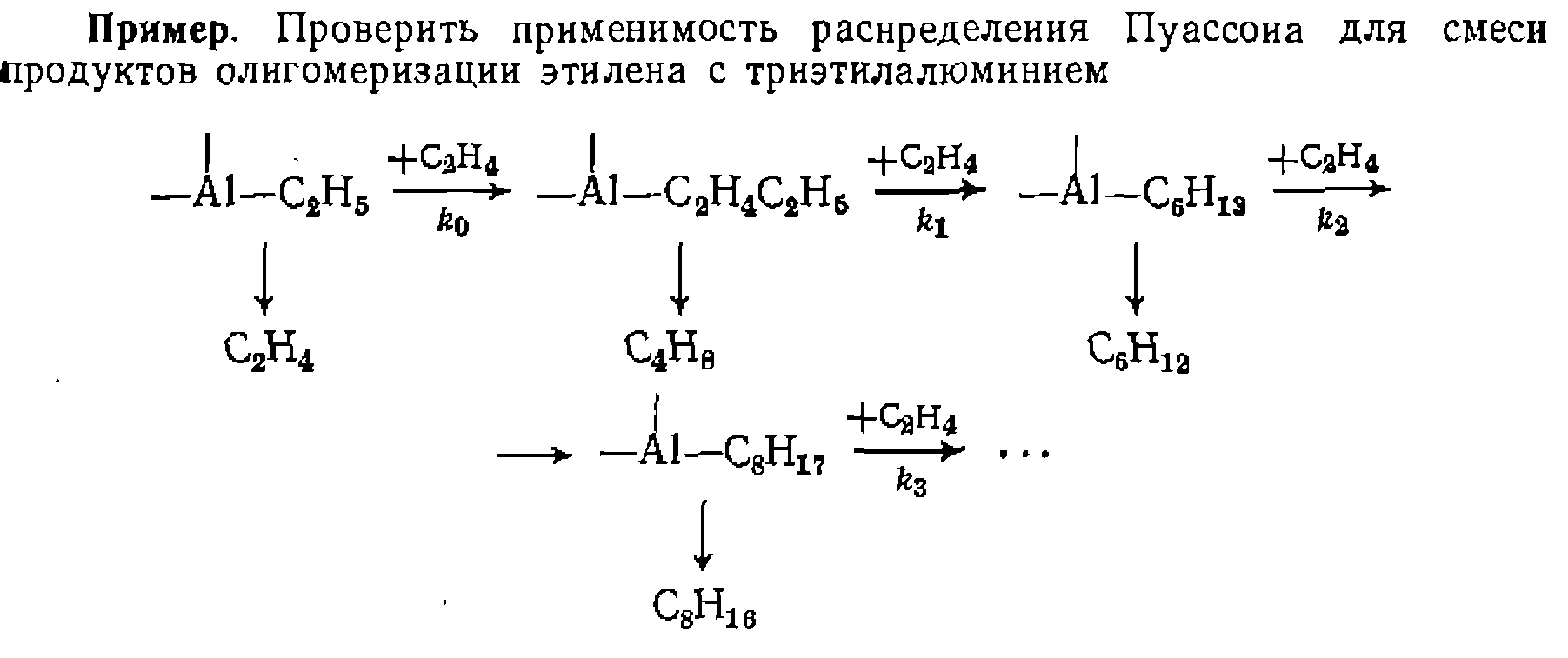
 предварительно найдено по -составу образующихся продуктов, то дальнейшая обработка кинетических данных сводится к поиску кинетического уравнения и констант первой стадии превращений. Это просто осуществить только в том случае, когда кинетика этой стадии не зависит от других стадий н не связана уравнениями баланса с продуктами реакции. Например, для последовательности реакций первого
предварительно найдено по -составу образующихся продуктов, то дальнейшая обработка кинетических данных сводится к поиску кинетического уравнения и констант первой стадии превращений. Это просто осуществить только в том случае, когда кинетика этой стадии не зависит от других стадий н не связана уравнениями баланса с продуктами реакции. Например, для последовательности реакций первого легко найти
легко найти  по интегральному уравнению
по интегральному уравнению  . То же самое можно сделать для последова
. То же самое можно сделать для последова или
или  , если кинетические-
, если кинетические- (распределение Флори —Пуассона). Здесь
(распределение Флори —Пуассона). Здесь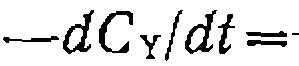
 , где последний множитель при неизменном объеме смеси имеет постоянную величину, равную
, где последний множитель при неизменном объеме смеси имеет постоянную величину, равную 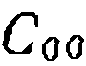
 Эти данные позволяют составить уравнения дифференциальной селективности и существенно облегчают дальнейшую» обработку эксперимента по кинетике реакции.
Эти данные позволяют составить уравнения дифференциальной селективности и существенно облегчают дальнейшую» обработку эксперимента по кинетике реакции.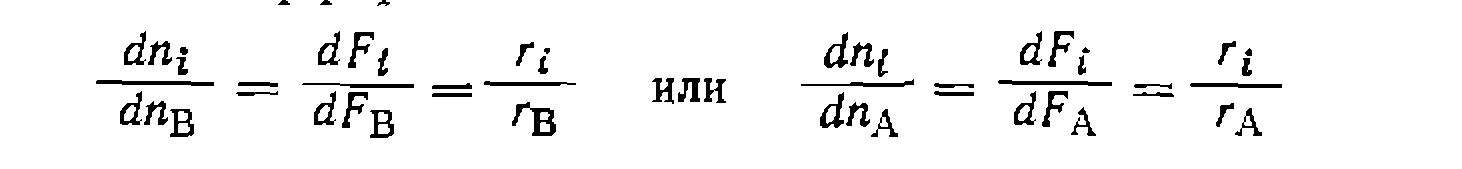
 в соответствующих случаях заменяют на
в соответствующих случаях заменяют на  или
или 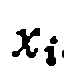
 , но выходам бензола
, но выходам бензола  и толуола
и толуола  при разных разбавлениях водяным наром н общем давлении ОД МПа:
при разных разбавлениях водяным наром н общем давлении ОД МПа: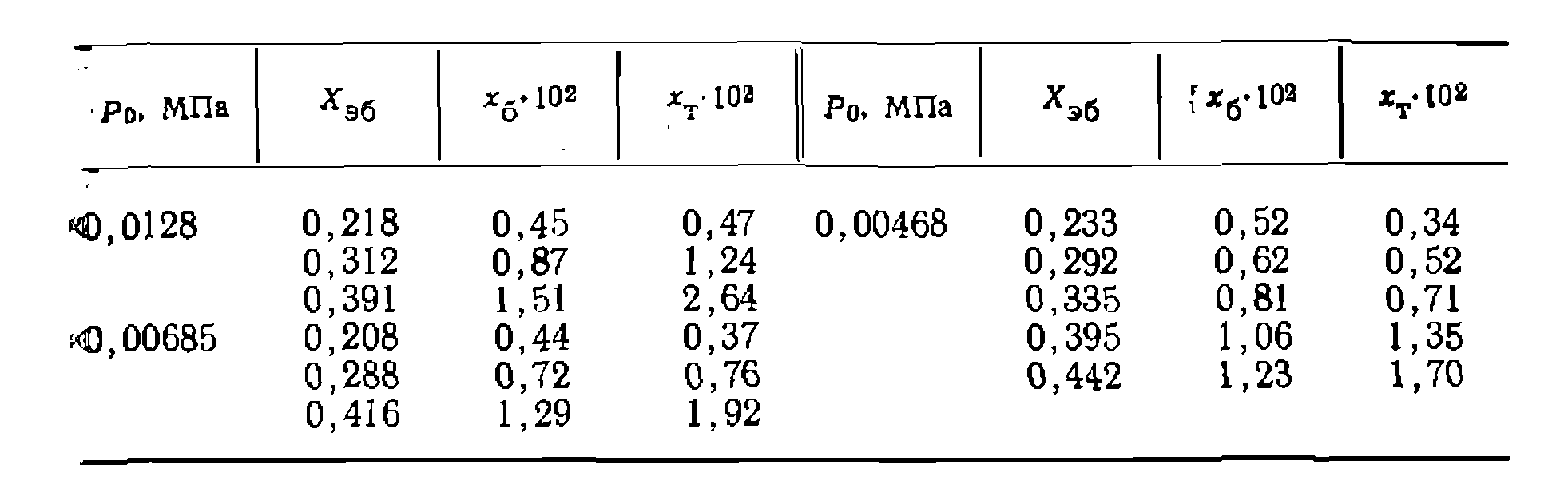
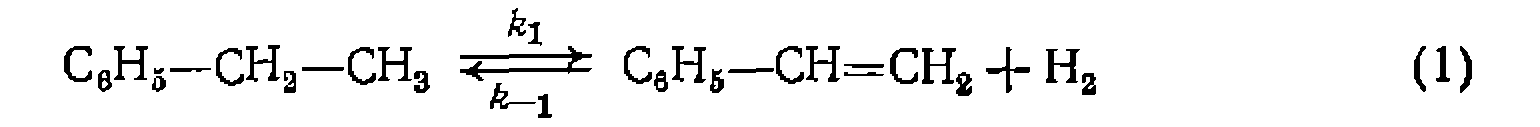
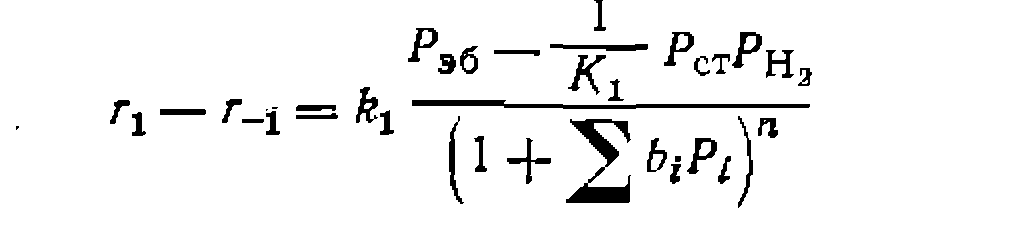
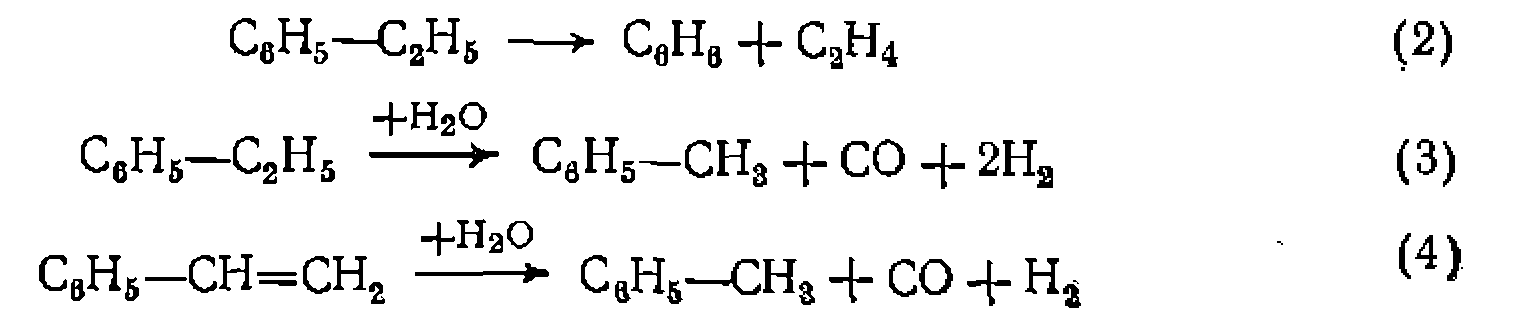
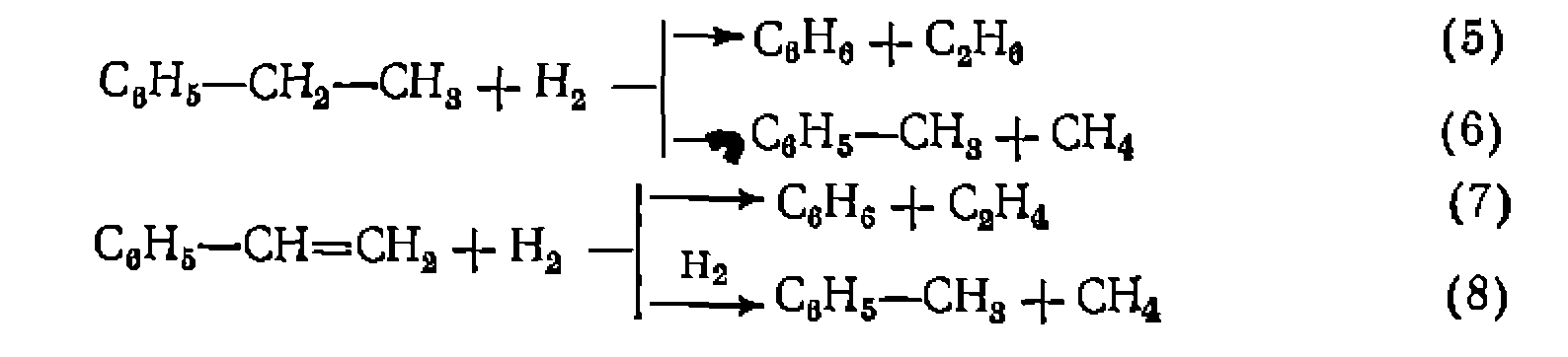
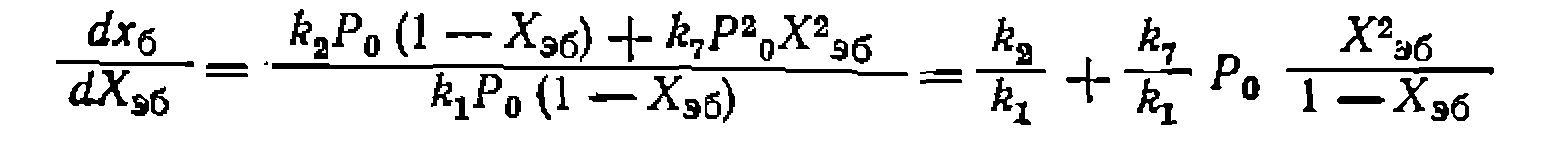
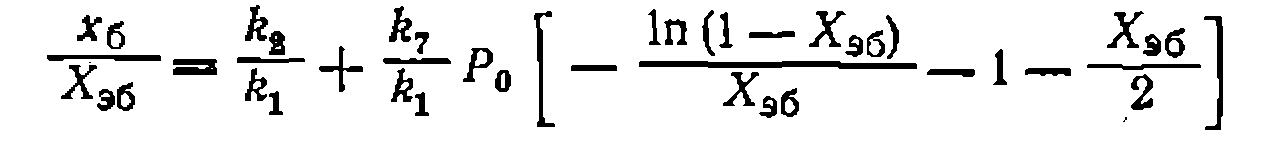
 J
J  *
* констант:
констант:  ,
,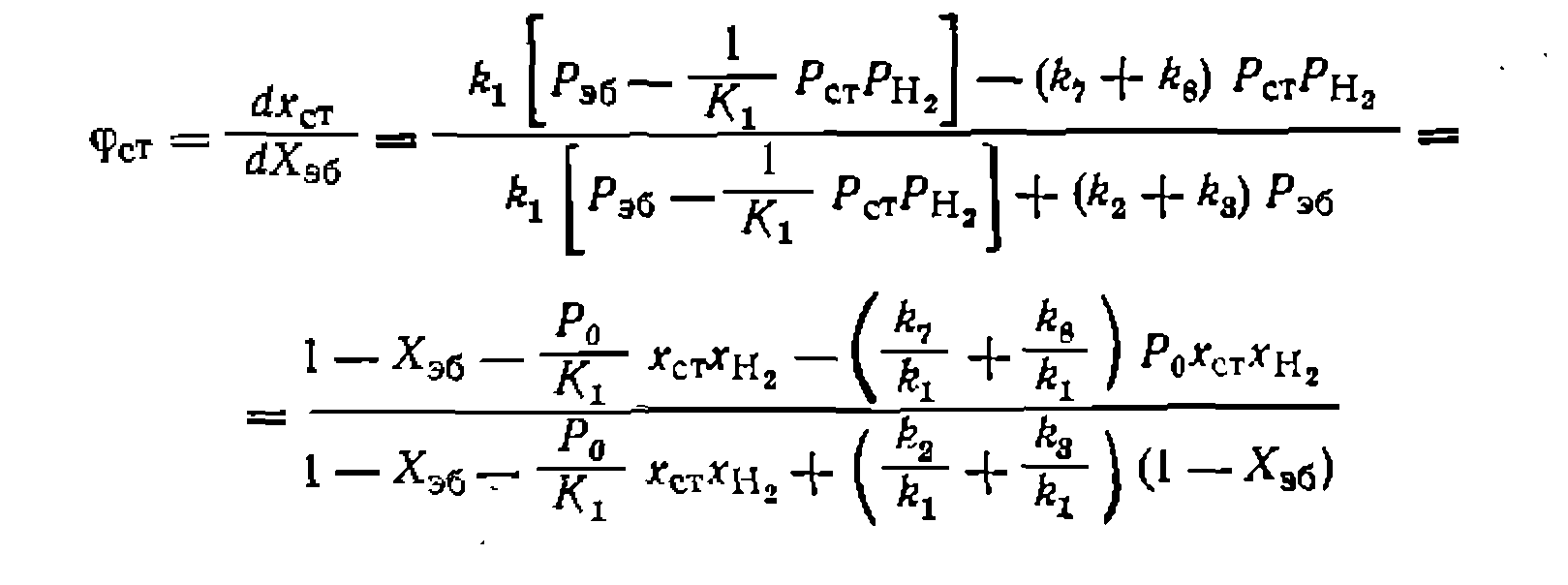


 и Е2-мехаинзмах замещения и отщепле
и Е2-мехаинзмах замещения и отщепле