
|
|
ПОСТРОЕНИЕ КИНЕТИЧЕСКИХ УРАВНЕНИИ
Подобно предыдущему, некоторые сложные реакции состоят лишь из элементарных реакций. Примером их является параллельное превращение RC1 в ROHи олефин по механизмам SN2 и E2 или обратимая реакция RBr+I=RI+Brесли она протекает по механизму SN2-замещения. Построение их кинетических уравнений осуществляется очень просто, например в первом случае
а во втором:
В большинстве случаев, однако, органические реакции являются неэлементарными, т. е. состоящими из некоторой совокупности элементарных стадий, протекающих при участии или с образованием промежуточных частиц (свободные атомы или радикалы, отрицательно или положительно заряженные ионы,, ион-радикалы) или комплексов (с катализатором, растворителем и др.). Под элементарной стадией понимают необратимое или обратимое превращение, протекающее через единственное переходное состояние. Совокупность их, т. е. механизм реакции, может быть линейной, разветвленной или замкнутой (рис. 12). Отметим, что в литературе элементарные реакции нередко называют простыми, а неэлементарные — сложными. В этой книге .классификация на простые и сложные реакции соотнесена с их стехиометрией или химизмом, а не с механизмом превращений. Гипотезу о механизме неэлементарных реакций выдвигают на основе имеющихся теоретических представлений и их дальнейшего развития для изучаемой системы. С этой же целью Рис. 12. Схема линейного (а), замкнутого{б)и разветвленного (в) маршрутов неэлементарных реакций.
важно привлечь физические и физико-химические методы идентификации промежуточных частиц или комплексов (спектры ЭПР, ЯМР, УФ, ИК и др.), или использовать литературные данные. Необходимое условие правильного составления механизма ‘состоит в том, что при -суммировании уравнений всех стадий промежуточные частицы и комплексы должны сокращаться, давая в итоге стехиометрическое уравнение реакции. Из гипотезы о механизме реакции далее выводят ее кинетическое уравнение, имея в виду, что для каждой элементарной стадии верен простой вид уравнения скорости, вытекающий из теории элементарных реакций. Для каждой из элементарных реакций сохраняется и понятие молекул яркости, равной числу участвующих в ней кинетически независимых молекул, частиц или комплексов. Наиболее общий подход к кинетическому описанию процесса состоит в его представлении как системы дифференциальных уравнений для скоростей превращения ключевых веществ данной совокупности элементарных реакций. Для этого вначале проводят стехиометрический анализ системы, подобный изложенному во введении, определяют число независимых элементарных стадий (базис реакций) и выбирают ключевые молекулы, комплексы или частицы. Для последних записывают скорости превращения через скорости элементарных реакций по типу = Так, для двухстадийной необратимой реакции А-р A+Y->B+Z, протекающей по механизму
имеются две независимые реакции и два ключевых вещества — А (или В) и X. Для этих независимых реакций уравнения скорости таковы:
При большом числе элементарных стадий такое описание кинетики оказывается весьма сложным. В действительности при большинстве неэлементарных реакций по промежуточным комплексам или частицам устанавливается так называемый квазистационарный режим.Он характеризуется тем, что скорость
Такой способ построения кинетических уравнений неэлементарных реакций, предложенный Боденштейном и развитый Н. Н. Семеновым, называется методом стационарных концентраций. Он позволяет исключить из кинетического описания процесса неизвестные концентрации промежуточных комплексов или частиц и получить одно или некоторый минимум дифференциальных уравнений скорости. Проанализируем кинетическое уравнение (II-37), соответствующее механизму (II-35). В знаменателе уравнения находится двучлен, содержащий скорости расходования промежуточной частицы X без ее концентрации. Если на первой стадии Zне выделяется, то член k-i\[Z]превратится в k-\, а при отсутствии реагента Yна второй стадии останется член k2 Уравнение (II-37) справедливо при сравнимой скорости обеих стадий, но часто бывает, что одна из них — самая медленная, лимитирующая скорость всего процесса.
Здесь скорость определяется первой стадией и не зависит от константы и концентрации реагента второй стадии (реакция имеет нулевой порядок по Y). В противоположном случаепренебрежение вторым членом знаменателя дает:
Здесь скорость лимитируется второй стадией, а на первой, быстрой стадии устанавливается равновесие. В подобных случаях наличия заведомо быстрых стадий, предшествующих лимитирующей, помимо или дополнительно к методу стационарных концентраций для нахождения концентраций промежуточных частиц и построения кинетических уравнений можно использовать метод равновесий:
и Е 1св-отщепления. В первых двух случаях вначале происходит гетеролитическое расщепление молекулы RC1и образовавшийся карбкатион быстро реагирует с нуклеофилом или отщепляет протон:
При одновременном протекании замещения и отщепления имеем: Из этого примера видно, что при параллельных реакциях, разветвляющихся на активной промежуточной частице, появляется взаимозависимость их кинетики. При Е1св-отщеплении первая стадия состоит в отщеплении протона основанием, после чего анион превращается с отщеплением Сl-:
Числитель уравнения (II-41) содержит разность произведений констант и концентраций реагентов (за исключением X), участвующих в прямых и обратных стадиях, причем при равенстве нулю любой цз констант обратных элементарных реакций процесс становится необратимым и второй член числителя исчезает. Уравнение (II-41) имеет ряд частных решений.Если в знаменателе можно пренебречь только одним из членов, имеем три варианта:
Здесь имеется единственная лимитирующая стадия, а на двух других устанавливается равновесие. Отметим важную особенность обратимых реакций, состоящую в их микроскопической обратимости, т. е. в протекании прямой и обратной реакций через те же элементарные стадии, но в противоположных направлениях. Это приводит к термодинамическому соответствию кинетики прямой и обратной реакций, которое .состоит в том, что приравнивание нулю скорости обратимой реакции (т. е. при равновесии) дает выражение, вытекающее из термодинамики. Так, для уравнений (П-41)- (11-47) получим:
Видно, что из кинетики прямой реакции однозначно следует кинетика обратной реакции. Например, первый порядок прямого превращения -соответственно уравнениям (II-46) и (II-47) предопределяет минус первый порядок по Yдля обратной реакции. Для построения кинетических уравнений сложных по механизму реакций большое значение приобрел метод маршрутов, развитый Хориути и Темкиным. Ранее уже говорилось, что сложение уравнений элементарных стадий должно приводить к сокращению Xi и давать в итоге стехиометрическое уравнение реакции. Для этого уравнения элементарных стадий приходится умножить на некоторое число — стехиометрическое число стадий04, удовлетворяющее условию:
Совокупность элементарных стадий с их стехиометрическими числами называют маршрутом реакции. В схемах механизмов (II-35) и (II-40) стехиометрические числа всех стадий равны единице и их маршруты представляют собой те же последовательности с проставленными справа Однако гипотеза о механизме реакций предполагает, что неэлементарные и сложные реакции могут протекать через ряд одинаковых нли разных стадий с теми же или иными промежуточными комплексами или частицами. Число независимых маршрутов, описывающих механизм реакций, называется базисом маршрутов и равно разности стехиометрически независимых стадий (базис реакций) и промежуточных комплексов или частиц:
Так, схемы механизмов (II-35) и (II-40) были одномаршрутными, так как N=2—1=3—2=1. Для таких одномаршрутных реакций скорость по маршруту г связана со скоростью элементарных стадий rj-r-jсоотношением:
Поскольку выражения для скорости элементарных стадий известны, то система таких уравнений для каждой стадии дает скорость по маршруту. Для одномаршрутной реакции (11-35) получим:
Многие сложные по механизму реакции могут быть много- маршрутными. Например, можно полагать, что реакция (II-40) протекает по двум маршрутам (I и II): Системы таких уравнений для каждой из элементарных стадий и маршрутов позволяют вывести кинетическое уравнение процесса. Например, для схемы (II-51) имеем систему уравнений
из которой далее выводится кинетическое уравнение. Ввиду . большой сложности построения кинетических уравнений для многомаршрутных реакций имеются специальные формализованные приемы, которые здесь не рассматриваются. Отметим, что маршрут реакции позволяет установить ее стехиометрическое уравнение. Так, с точки зрения стехиометрии или термодинамики безразлично, написать ли А=В или 2А=2В, уравнение реакции необходимо записывать как 2А=2В. В последнем случае для использования в кинетике константу равновесия надо записывать не через К= [B]/[A]', а так: К' =][В]2/[А]2.
До сих пор нам встречались лишь маршруты, состоящие из линейной последовательности стадий, когда при построении кинетических уравнений устраняются концентрации всех промежуточных частиц.
В случае замкнутых маршрутов, особенно характерных для каталитических и цепных реакций, одна из этих концентраций (например, катализатор в свободной форме) остается неизвестной, и для ее нахождения требуется дополнительное условие. При каталитических реакциях таковым является уравнение баланса по разным формам катализатора, рассматриваемое в гл. III и VI. Здесь мы рассмотрим близкий к этому случай, когда необходимо сведение баланса по разным формам реагентов. Дело в том, что в выведенных ранее уравнениях [Аi] означает действующую концентрацию или парциальное давление вещества именно в той форме, которая заключена в квадратные скоб- ки. Когда эта концентрация равна аналитической или общей концентрации или парциальному давлению вещества, т. е. когда вещество находится в смеси в единственной форме, то [А;] = Сi или Pi,и, например, кинетическое уравнение (II-37) преобразуется в такую форму: Если комплексы X и AYаналитически определяются вместе с А и Y, концентрации свободных форм реагентов в кинетическом .уравнении (11-55) необходимо выразить черезих суммарные концентрапии. Они связаны уравнениями балайса по всем формам реагентов;
При сравнимых концентрациях А и Yприходится решать совместно оба уравнения баланса, что дает сложное выражение для [А] и I[Y] и сложное кинетическое уравнение. Решение упрощается, когда один из реагентов находится в избытке, и можно считать, что [Y]=Cy. Это позволяет ограничиться балансом лишь по А и получить
Типичные примеры подобных явлений — щелочное дегидрохлорирование хлоргидринов и амидироваиие карбоновых кислот. При дегидрохлорировании хлоргидринов щелочь и хлоргид- рин находятся в двух формах Эти примеры показывают, что после построения первичных кинетических уравнений методом стационарных концентраций или маршрутов всегда требуется оценить возможность существования реагентов и катализаторов в разных формах и получить уточненный вид кинетического уравнения, учитывающий это явление. Во всех предыдущих кинетических уравнениях фигурировали константы скорости элементарных реакций, которые неред
где kэф = k-1/k2.,В уравнении (II39) имеются две константы, а определяется только одна (r=K1k2CaCy=kЭфСАСу, где кэф = K1k2).Для таких эффективных констант также находят из опытов эффективные пред экспоненты, энтропии и энергии активации, но из их величин уже нельзя делать определенных выводов о механизме реакций, так как они являются комбинацией соответствующих значений для истинных констант скорости и равновесия. Так, для имеем Эффективными называют и константы, включающие постоянные в условиях опытов концентрации реагентов, находящихся в большом избытке, или концентрации гомогенных катализаторов. Так, в уравнении (II-37) при большом избытке Yего концентрацию вводят в константу к2 и получают
Из этого уравнения выпала концентрация избыточного 'реагента, который в действительности влияет на скорость, но из-за его большого избытка реакция имеет по нему псевдонулевой порядок. Систему уравнений, описывающих изменение состояния химического процесса прн бесконечномалом варьировании его параметров, называют кинетической моделью. В стационарных условиях она состоит из системы дифференциальных уравнений для скоростей превращения ключевых веществ, т. е.
подведение балансов по разным формам реагентов и катализаторов. Когда этн балансы имеют сложный вид, можно не вводить их в уравнения скоростей, а давать отдельно. При решении кинетических моделей, в том числе при обработке опытов, обычно требуется сократить число переменных (кроме времени или условного времени контакта) до числа ключевых веществ в данной системе. Этими переменными являются концентрации, парциальные давления или выходы ключевых веществ, в некоторых случаях — полнота реакции Хj При этом другие переменные заменяются на ключевые по уравнениям баланса реакции. Так, для простой реакции 2А—>В, протекающей в жидкой фазе без изменения объема по кинетическому уравнению r=kC2а, в зависимости от выбора переменных можно составить кинетическую модель в трех формах:
где x =Сi—С; о/vi,- является полнотой реакции, отнесенной к единице объема. В более сложных случаях, при замене лишних переменных нужно учитывать распределение вещества между фазами, про- тивоточный или перекрестный поток реагентов, отгонку продуктов из смеси и другие варианты осуществления процесса либо исследования его кинетики. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|








 Примерами неэлементарных реакций, аналогичных схеме (II-35), являются нуклеофильные процессы SNl-замещения, Е1
Примерами неэлементарных реакций, аналогичных схеме (II-35), являются нуклеофильные процессы SNl-замещения, Е1





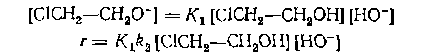

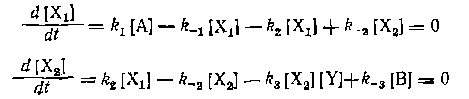

 Здесь на одной из стадий устанавливается равновесие, а две другие сравнимы по скорости. Когда в знаменателе можно пренебречь двумя членами, возможны тоже три варианта:
Здесь на одной из стадий устанавливается равновесие, а две другие сравнимы по скорости. Когда в знаменателе можно пренебречь двумя членами, возможны тоже три варианта:






 Для многомаршрутной реакции скорости элементарных стадий и скорости по маршрутам связаны уравнением
Для многомаршрутной реакции скорости элементарных стадий и скорости по маршрутам связаны уравнением




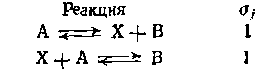



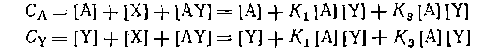

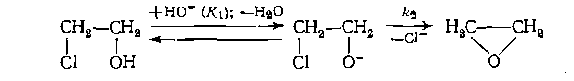

 При амидировании карбоновых кислот образуется неактивная соль:
При амидировании карбоновых кислот образуется неактивная соль:



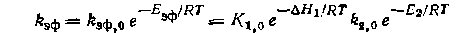
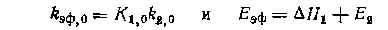


 Как мы видели выше, при построении кинетической модели необходимы гипотеза о схеме превращений, механизме реакций и
Как мы видели выше, при построении кинетической модели необходимы гипотеза о схеме превращений, механизме реакций и
