
|
|
Пример. Для irap а л ЛеЛьных реакцийИмея такие данные, можно количественно описать состав «образующихся продуктов. Так, при хлорировании-или при других реакциях замещения любых парафинов в отсутствие последовательных превращений получим мольные доли монозамещен- ных продуктов: Рис. 22. .Соотношение продуктов при па- раллельных реакциях одинакового порядка. ференциальному
Если по изложенной методике определено соотношение констант скорости параллельных реакций одинакового порядка, то кинетическая обработка результатов опытов сводится к поиску суммы констант и концентрационных функций по единственному диф- уравнению расходования основного реаген- Такая обработка аналогична рассмотренной выше для простых реакций, причем по сумме констант и ранее найденному их соотношению находят каждую константу в отдельности. Метод конкурирующих реакций применяется для изучения относительной реакционной способности разных веществ А] и А2 по отношению к общему реагенту Y:
Во всех случаях, если анализ ведут по продуктам В и С, можно заменить
При большом избытке Ai и Аг по отношению к Y, когда
Решение интеграла при неизменном объеме смеси дает:
При наиболее часто встречающемся одинаковом порядке реакций по Y (или молекулярности по X) при первом порядке по Ai и А2 имеем: Следует иметь в виду, что истинное соотношение констант (реакционная способность) получится только для гомогенных гомофазных условий проведения процесса или для реакций, протекающих в той же фазе, где находятся реагенты В противном случае накладывается влияние неодинаковой сорбции веществ Изложенная методика широко применяется для изучения относительной реакционной способности веществ при разных реакциях (сульфирование, нитрование, хлорирование и др.). Совместное использование методов конкурирующих реакций и реакций одинакового порядка позволяет одновременно получить данные об относительной реакционной способности двух веществ и каждого из положений в молекуле их. Например, при какой- либо реакции замещения в ароматическое ядро, проведенной на смеси бензола и толуола, можно определить концентрации всех образовавшихся веществ:
По количеству замещенного бензола, сумме производных толуола н по уравнениям (II-76) и (II-77) легко найти суммарное соотношение констант. Если его обозначить через
где
Найти соотношение суммарпых скоростей хлорироаания изобутана и пропана и относительную реакционную способность разных атомов водорода в их молекулах. Наконец, сравниваем реакционную способность атомов водорода в метальных группах пропана и изобутана:
Относительную реакцнопную способность разных атомов водорода в молекулах пропана и изобутана находим по формуле (11-74):
По этому уравнению методом наименьших квадратов находим: Поскольку углеводороды находятся в значительном избытке но отношению к хлору н реакция протекает без изменения объема смеси, для расчета соотиошепия суммарных скоростей замещения используем уравнение (II-77): и уравнение скорости образования продукта В (скорость расходования реагента Y):
По этому выражению находим из опытов £i/&2> после чег( составляем баланс по реагенту А:
Разделяем переменные и интегрируем, принимая Сс,о = 0:
При порядках реакции, равных стехиометрическим коэффициентам, имеем дифференциальное уравнение Аналогичным образом можно по составу продуктов находить соотношение констант скорости и для других систем параллельных необратимых реакций, после чего обработка результатов опытов по их кинетике осуществляется по единственному дифференциальному уравнению скорости. Рассмотрим эту процедуру для такого практически важного примера: Это уравнение при известном соотношении ется численно. Наиболее целесообразно вести поиск Из него или из ранее найденного соотношения продуктов получаем выражение для интегральной селективности:
Для только что рассмотренной системы реакций, как и для любых параллельных превращений, легко составить уравнение дифференциальной селективности: Видно, что в данном случае селективность по продукту В зависит от начальной концентрации реагента Y и от степени его конверсии, При этом второе слагаемое знаменателя — положительная величина, которая при В свою очередь, из полученного уравнения селективности легко составить выражения для выходов или концентраций образующихся продуктов:
Подобные уравнения состава продуктов и селективности можно получить независимо от кинетического исследования, и они имеют важное значение для решения ряда практических задач. ИНТЕГРАЛЬНЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ ПОСЛЕДОВАТЕЛЬНЫХ РЕАКЦИЙ Из необратимых реакций этого типа наиболее интересны последовательные реакции первого порядка
и последовательно-параллельные превращения, имеющие общий второй реагент:
К последним относятся реакции последовательного замещения атомов водорода при хлорировании, алкилировании и др.
последовательного присоединения к полиолефинам и ароматическим соединениям
а также последовательного удлинения молекулярной цепи при олигомеризации:
Если стехиометрические коэффициенты и порядки (молеку- лярности) по реагентам каждой стадии для всех этих реакций равны единице, то при их необратимости получим для первого промежуточного продукта
где и —текущие концентрации исходного реагепта и первого промежуточного продукта. Для периодических условий реакции или при проведении ее в реакторе идеального вытеснения последнее выражение надо проинтегрировать. Для этого вводим вспомогательную переменную
При постоянстве объема смеси во время реакции интегрирование от
которое преобразуется в такой вид:
Здесь CJCnn можно заменить на 1—Ха или же ввести моль-
ные доли
и получить
Следовательно, содержание (выход) первого промежуточного продуктазависит от доли непревращенного исходного реагента (или ющих стадий реакции. При
Следовательно, при неизменном объеме смеси случае, вводя ту же вспомогательную переменную Последовательно-параллельные реакции имеют некоторые важные особенности. Для них часто бывает, что второй реагент вначале превращается в активную промежуточную частицу Далее для последовательно-параллельных реакций значение
гента Y. В противном случае его рассчитывают по составу ш> лученной смеси из уравнений баланса
где Таким образом, при изучении состава продуктов последовательных реакций следует изображать его графически в коорди^ натах кроме того, в координатах тивность последовательных реакций выражают как функцшо
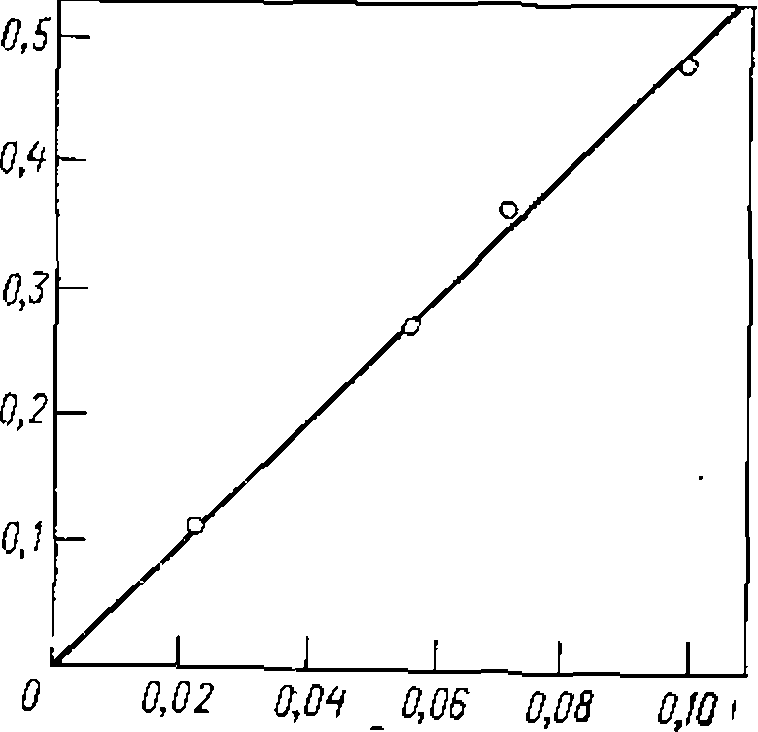
Построить графики зависимостей найти соотношение констант скорости последовательных стадий Для построения • графиков находим для каждого опыта
Ияпбпажаем опытные данные в координатах
ной обработки опытов применяем уравнение (II-80), подбираяна ЭВМ нелинейным методом наименьших квадратов наилучшие оценки Функции распределения. При большом числе стадий последовательно-параллельных реакций в полученной смеси содержится много веществ с разной степенью замещения, олигомеризации или полимеризации. Состав такой смеси изображают графически в виде кривойраспределения, откладывая мольную долю данного продукта Количественное описание этой зависимости, частным случаем которой были формулы (II-79) и (11-80) для первого промежуточного продукта, вытекает из системы, дифференциальных уравнений для каждого из продуктов
и из уравнения баланса (II-82). По ним на цифровой ЭВМ по> известным экспериментальным данным подбирают оптимальные- значения коэффициентов распределения для последующих расчетов. Rчастном случае равенства всех констант скорости, т. е. при
Это уравнение дает распределение Пуассона, оказавшееся применимым к процессу олигомеризации дикарбоновых кислот те* гликолей, этилена, а в некоторых случаях— и этиленоксида. Оно графически представлено на рис. 25 в виде кривой 1 для средней степени олигомеризации ■ т—Ю. Если соотношения
Обработка данных по кинетике последовательных реакций. По формуле (II-87) рассчитываем для тов, а
Сравнение экспериментальных и расчеа^ых данных показывает их достаточную близость, причем ' наблюдаемые отклонения, видимо, происходят от неточности определения 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
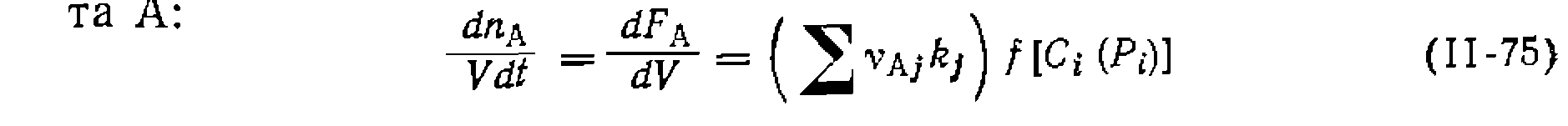

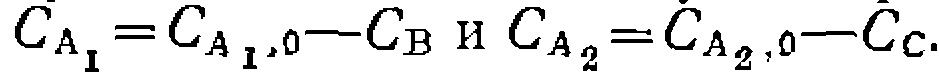

 и
и  практически постоянны, решение интеграла таково:
практически постоянны, решение интеграла таково: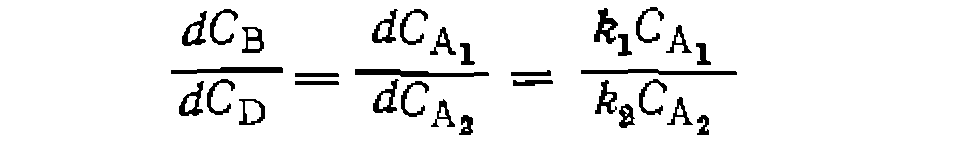
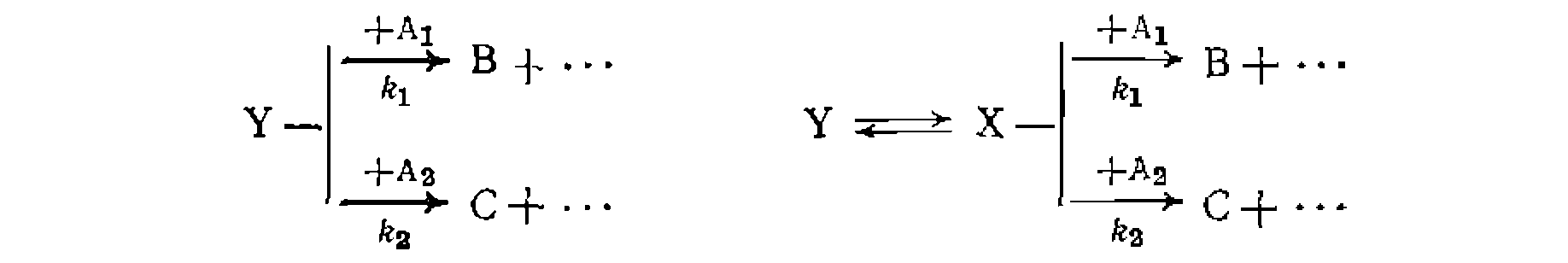
 и
и  на гетерогенном катализаторе или влияние разной их растворимости в фазе Y, где протекает реакция.
на гетерогенном катализаторе или влияние разной их растворимости в фазе Y, где протекает реакция.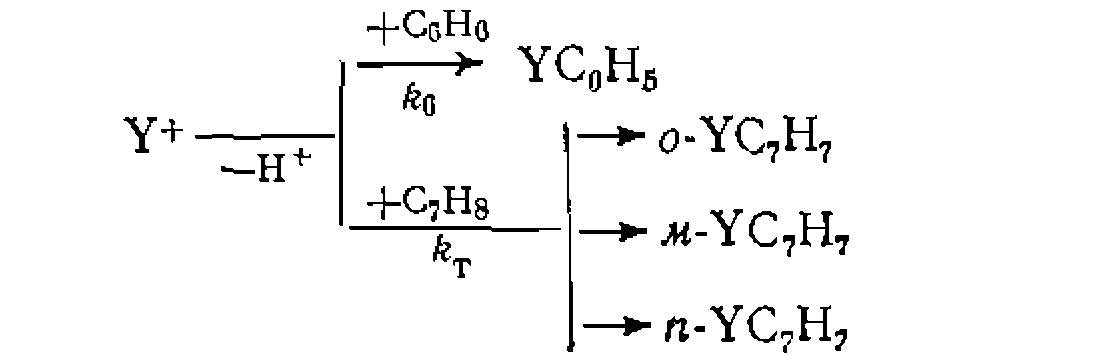
 , то с учетом наличия в молекуле толуола двух орто- и .мега-положений и одного л ара-положения, а также шести одинаковых центров замещения в молекуле бензола, вычисляют реакционную способность каждого из положений молекулы толуола по-сравнению с одним из реакционных центров незамещенного бензола
, то с учетом наличия в молекуле толуола двух орто- и .мега-положений и одного л ара-положения, а также шести одинаковых центров замещения в молекуле бензола, вычисляют реакционную способность каждого из положений молекулы толуола по-сравнению с одним из реакционных центров незамещенного бензола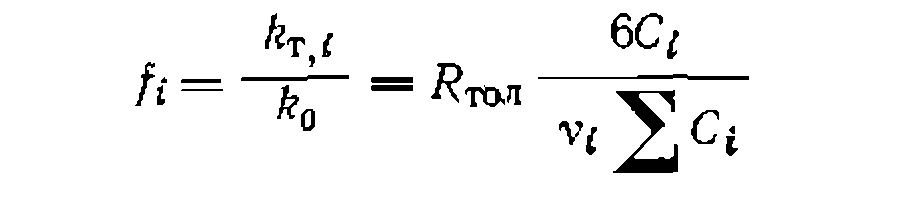
 и
и  —число соответствующих положений и концентрации изомеров замещенного толуола. Эти величины называют факторами парциальной скорости замещения в ортомета- и пара-положения
—число соответствующих положений и концентрации изомеров замещенного толуола. Эти величины называют факторами парциальной скорости замещения в ортомета- и пара-положения  . Подобным образом, например, хлорируя смесь парафинов, определяют не только суммарную относительную скорость их хлорирования, но и реакционную способность каждого из атомов водорода.
. Подобным образом, например, хлорируя смесь парафинов, определяют не только суммарную относительную скорость их хлорирования, но и реакционную способность каждого из атомов водорода.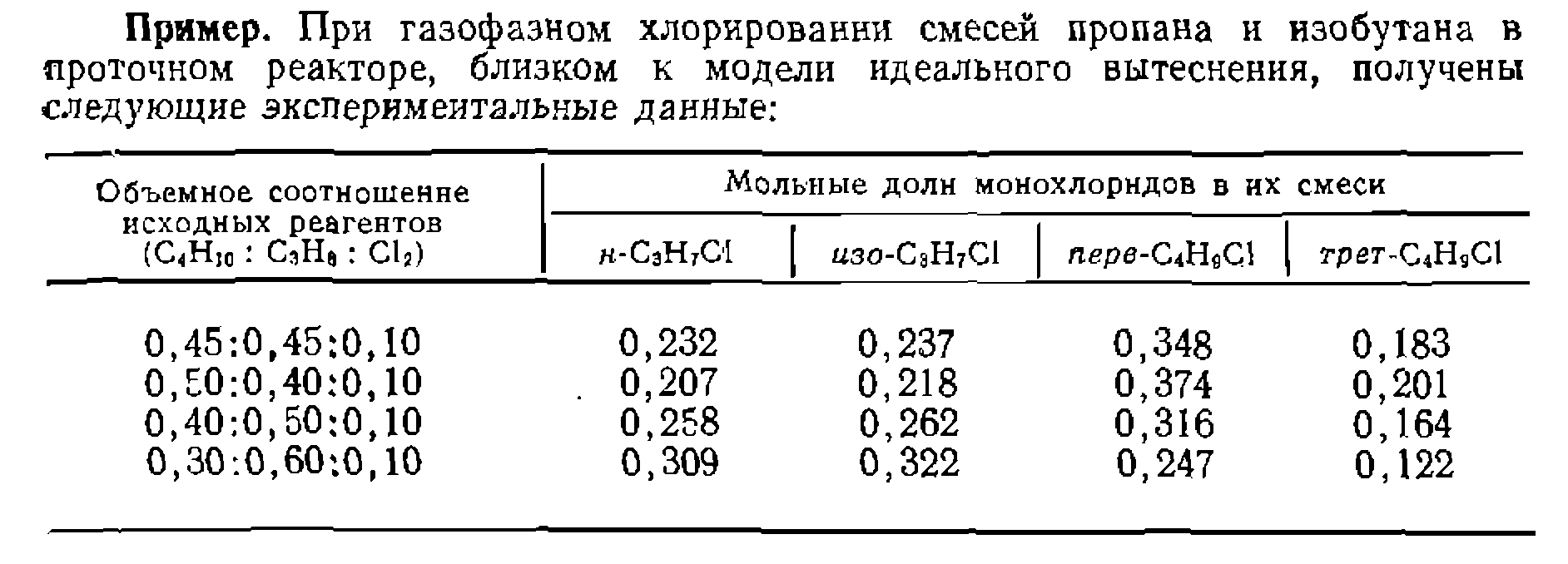
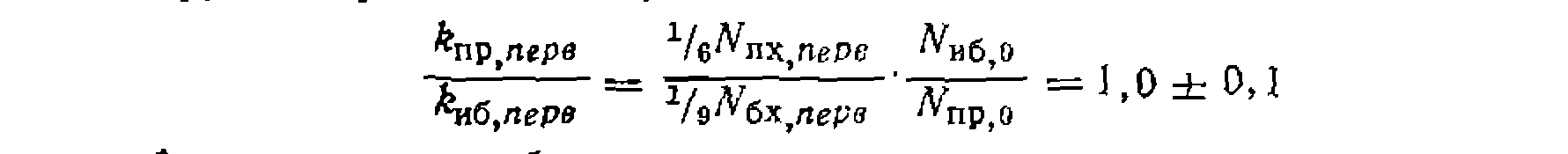

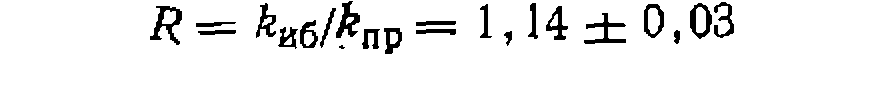
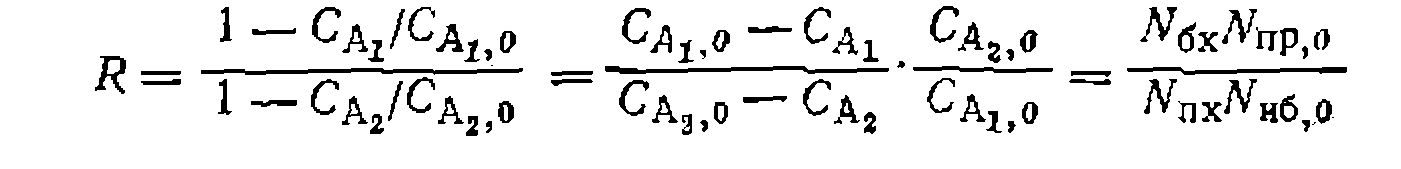
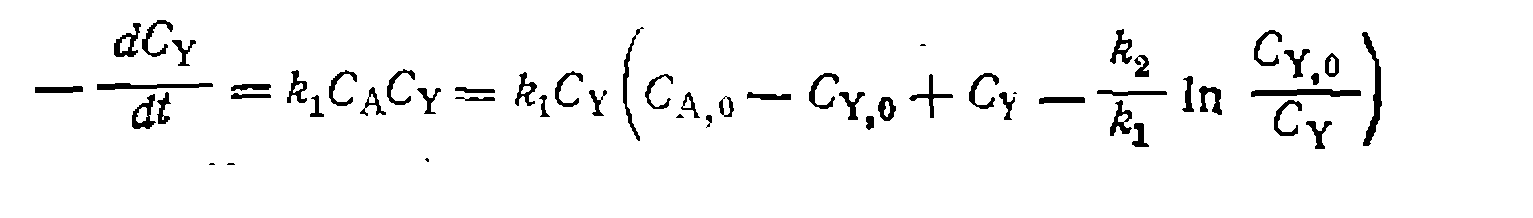
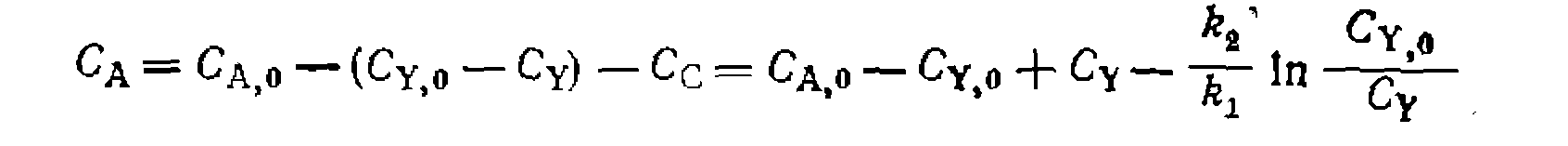

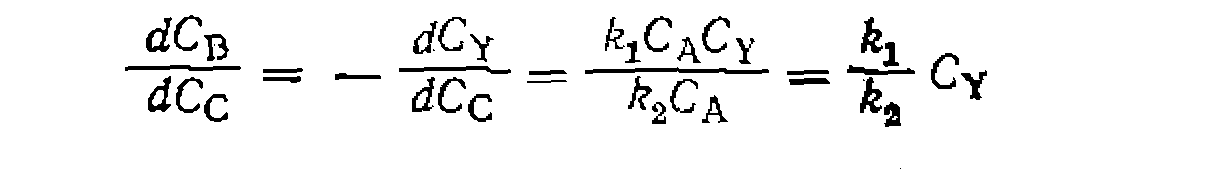

 интегриру
интегриру на цифровой ЭВМ с помощью нелинейного МНК. По значениям
на цифровой ЭВМ с помощью нелинейного МНК. По значениям  и
и  вычисляют значение
вычисляют значение  ; закоррелированность констант
; закоррелированность констант  и
и  снижается при этом по сравнению с поиском констант по кинетической модели без предварительного нахождения
снижается при этом по сравнению с поиском констант по кинетической модели без предварительного нахождения 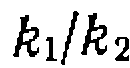
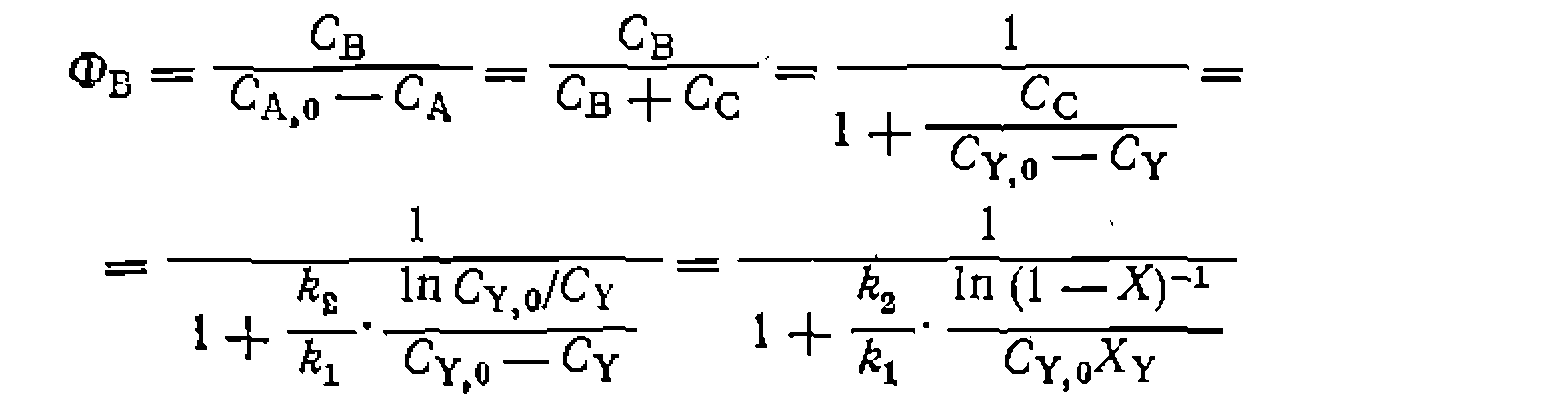
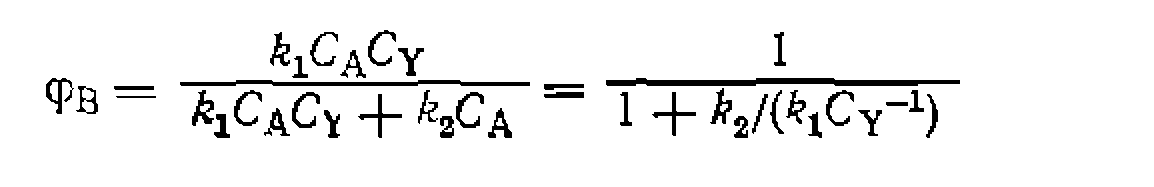
 (а следовательно, и при
(а следовательно, и при  стремится к
стремится к 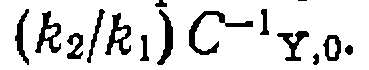 Таким образом,' при
Таким образом,' при  селективность имеет значение, промежуточное между 0 и 1, но не равное им, что является характерным признаком параллельных реакций, как и других, систем, включающих параллельные пути расходования основного реагента А.
селективность имеет значение, промежуточное между 0 и 1, но не равное им, что является характерным признаком параллельных реакций, как и других, систем, включающих параллельные пути расходования основного реагента А.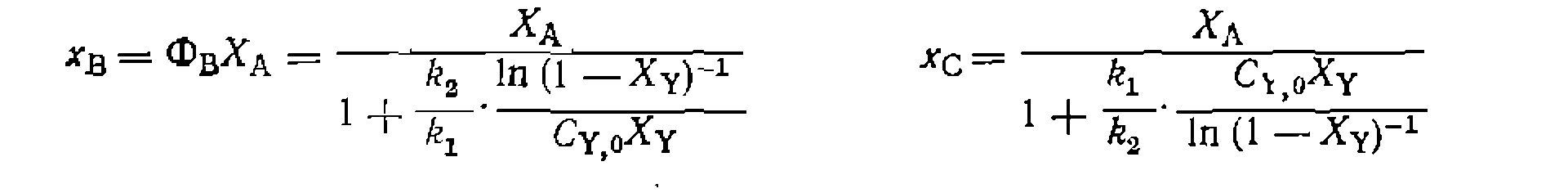
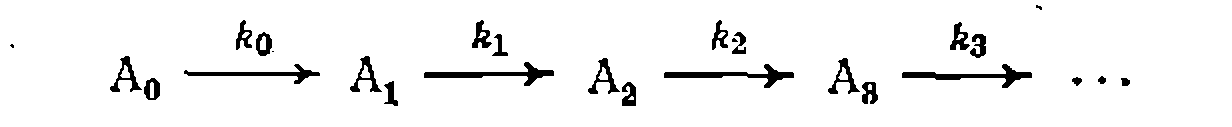
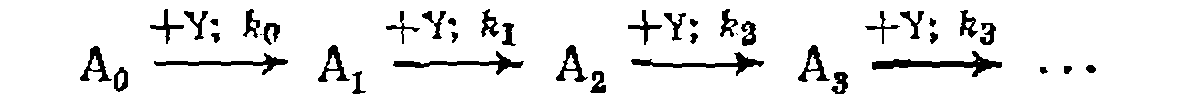
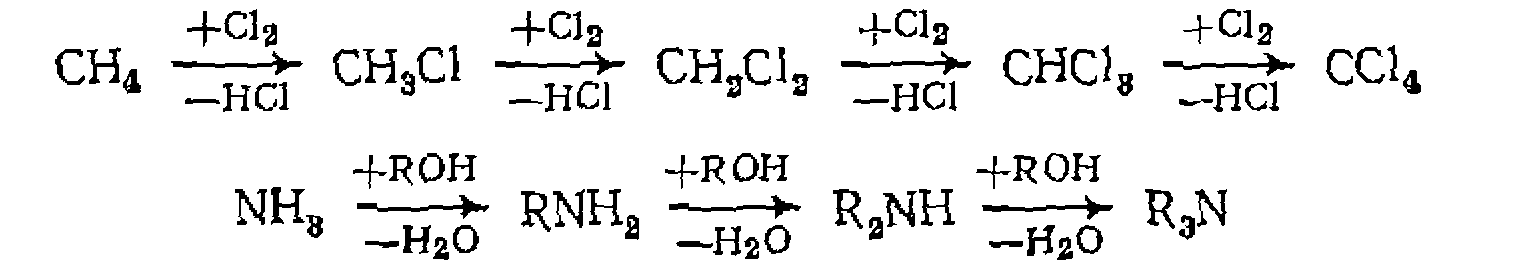
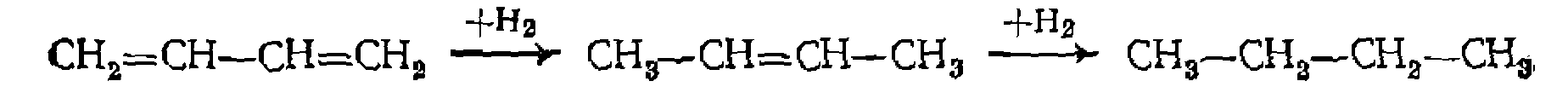
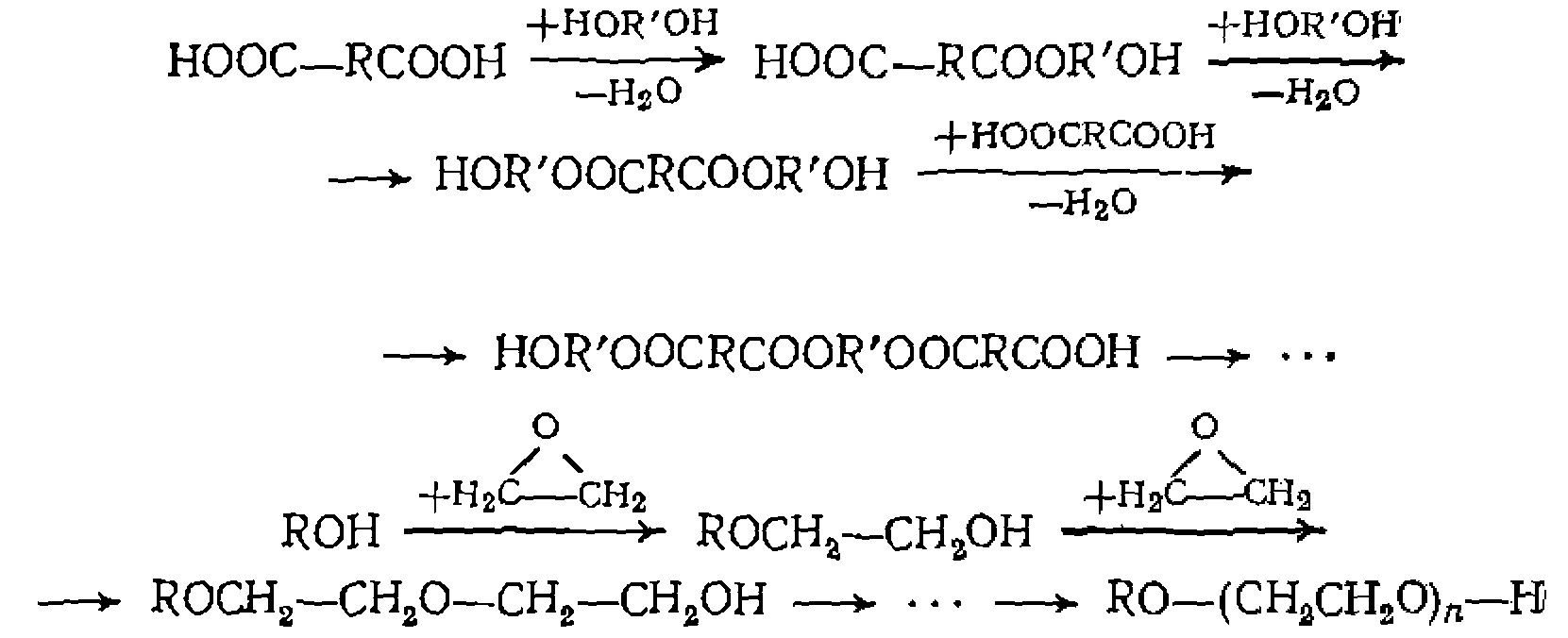
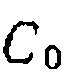
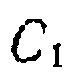
 и делаем следующие преобразования:
и делаем следующие преобразования: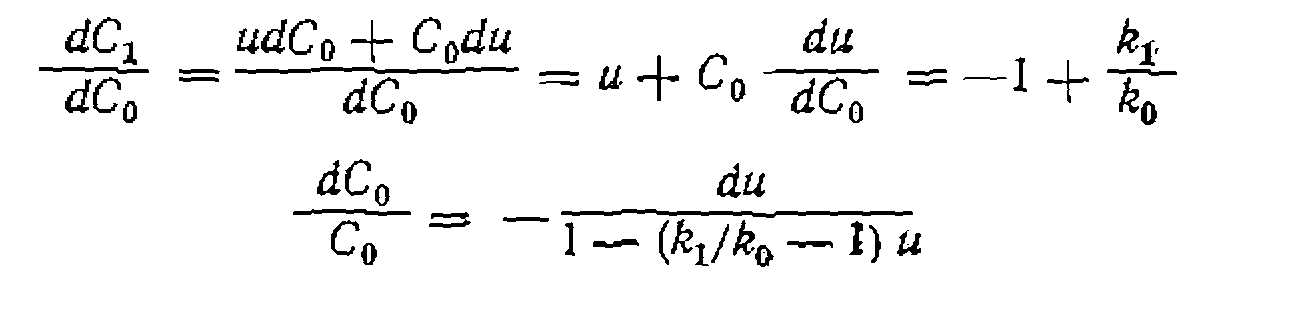
 до
до  и от начальной концентрации основного реагента
и от начальной концентрации основного реагента  до
до  дает выражение
дает выражение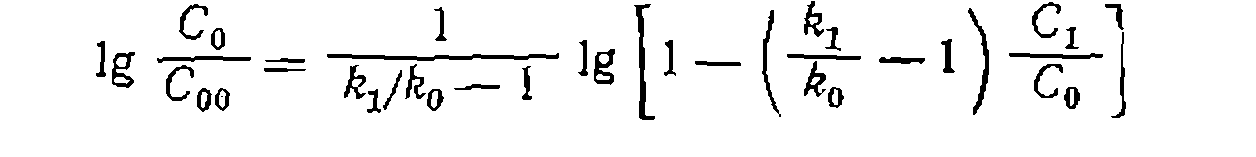
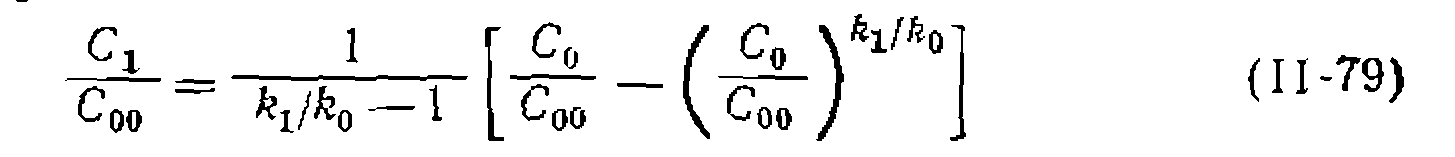
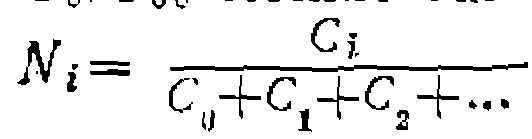
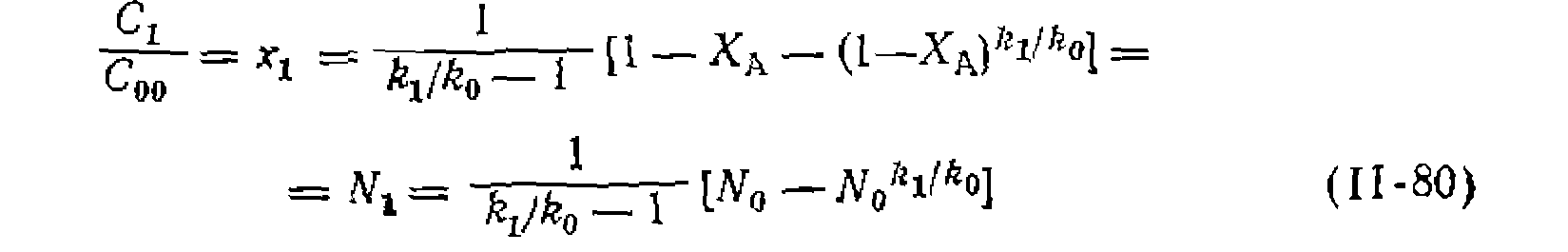
 и от соотношения констант скорости соответству
и от соотношения констант скорости соответству уравнения (II-79) и (11-80) неверны. В этом
уравнения (II-79) и (11-80) неверны. В этом
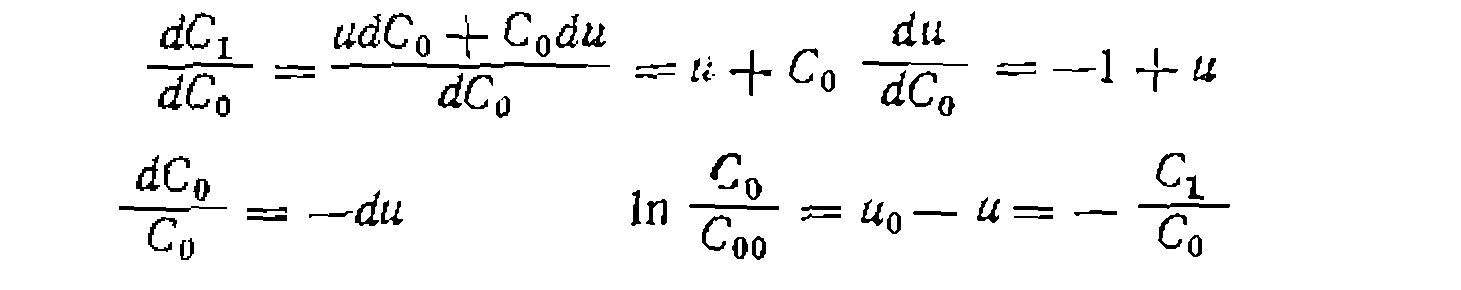
 , получим:
, получим: при хлорировании,
при хлорировании,  при алкилировании и т. д.), которая атакует каждый из последовательных продуктов реакции, причем эта элементарная стадия и определяет соотношение продуктов. В результате независимо от вида кинетических уравнений реакций оказываются справедливыми выведенные выше уравнения, по которым определяют соотношение констант элементарных реакций.
при алкилировании и т. д.), которая атакует каждый из последовательных продуктов реакции, причем эта элементарная стадия и определяет соотношение продуктов. В результате независимо от вида кинетических уравнений реакций оказываются справедливыми выведенные выше уравнения, по которым определяют соотношение констант элементарных реакций. и мольные доли всех продуктов зависят от мольного соотношения вступившего' в реакцию общего реагента Y ко всему количеству вещества А, так -как при недостатке Y невозможно получить высокое значение
и мольные доли всех продуктов зависят от мольного соотношения вступившего' в реакцию общего реагента Y ко всему количеству вещества А, так -как при недостатке Y невозможно получить высокое значение  Это мольное соотношение, которое мы обозначим
Это мольное соотношение, которое мы обозначим  , можно приравнять мольному соотношению взятых реагентов |3y только при полной конверсии реа-
, можно приравнять мольному соотношению взятых реагентов |3y только при полной конверсии реа-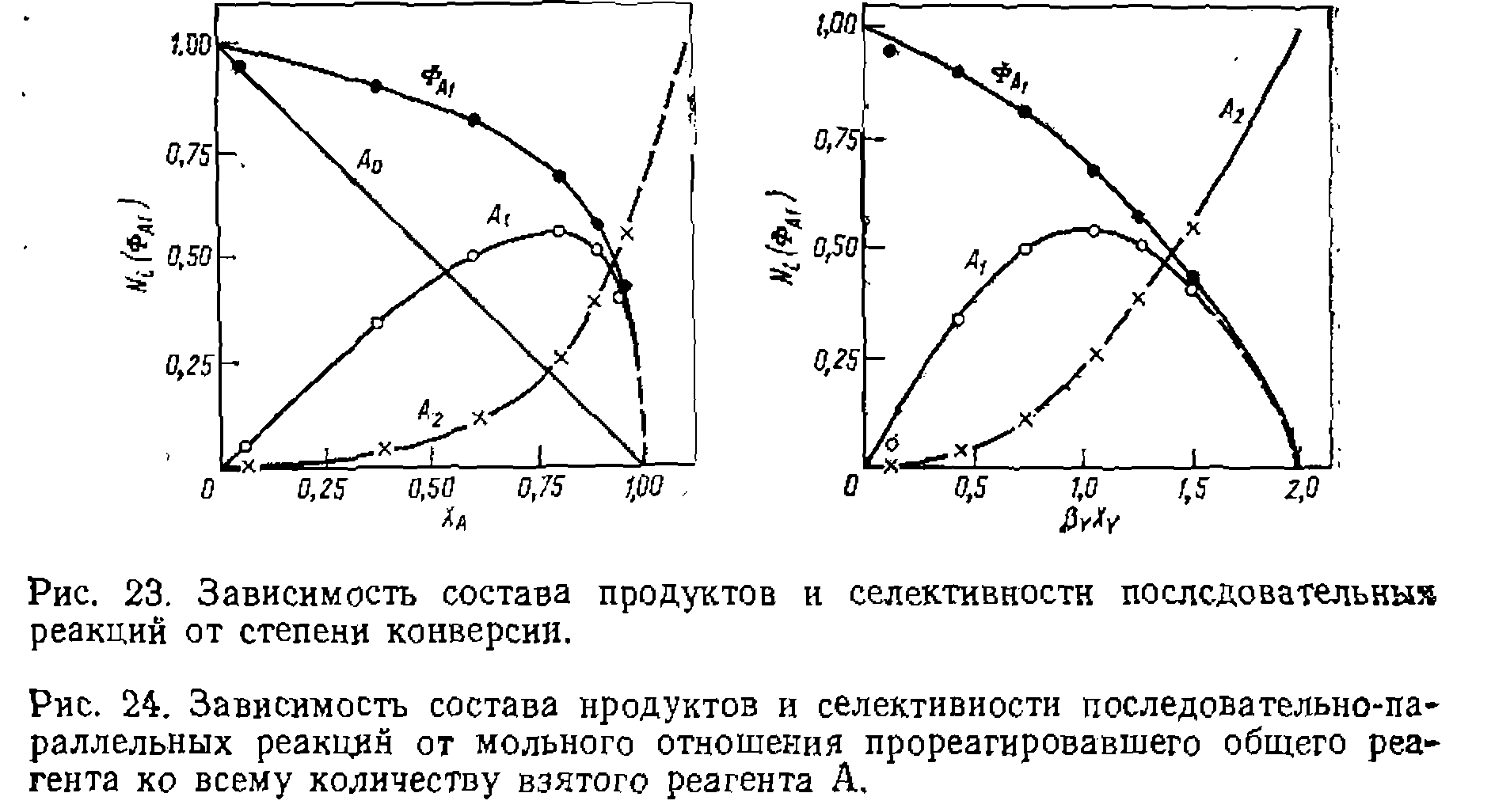
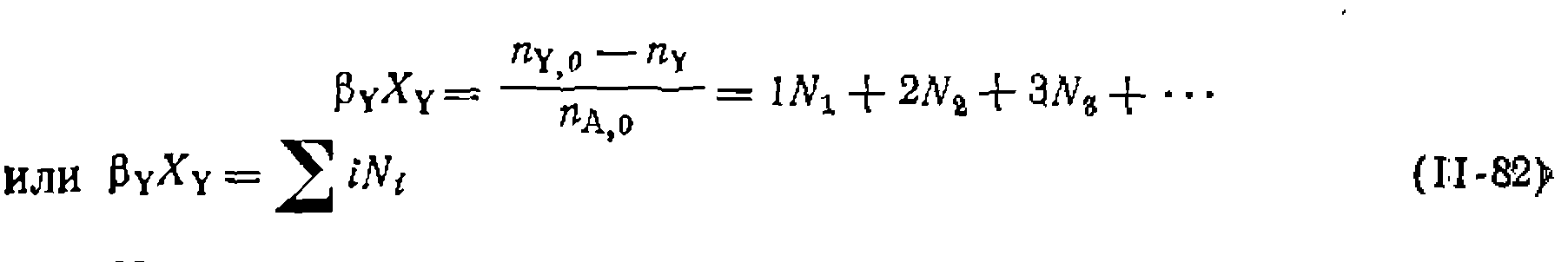
 —мольная доля продукта, содержащего I атомов, групп или фрагментов реагента Y.
—мольная доля продукта, содержащего I атомов, групп или фрагментов реагента Y. , а для последовательно-параллельных реакций*
, а для последовательно-параллельных реакций* . Соответственно и селек
. Соответственно и селек или
или  . При этом селективность по первому промежуточному продукту при
. При этом селективность по первому промежуточному продукту при  или
или  стремится к единице, что является убедительным признаком последовательной схемы превращений.
стремится к единице, что является убедительным признаком последовательной схемы превращений.
 и
и 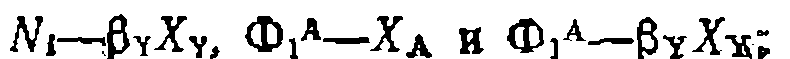
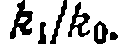

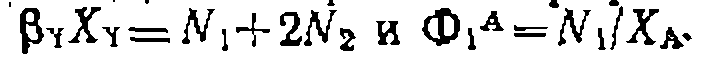

 (рис. 23) ►
(рис. 23) ► (рнс. 24),
(рнс. 24),  (рис. 23 и 24). Для количествен
(рис. 23 и 24). Для количествен . В результате находим
. В результате находим  Исходя из этого значения
Исходя из этого значения  и формулы (11-80) построены кривые рнс. 23 и 24, из которых видно их хорошее соответствие эксперименту (точки).
и формулы (11-80) построены кривые рнс. 23 и 24, из которых видно их хорошее соответствие эксперименту (точки). против числа замещения или присоединения, соответствующего образованию этого продукта, т. е. L. При этом среднюю степень замещения или олигомеризации
против числа замещения или присоединения, соответствующего образованию этого продукта, т. е. L. При этом среднюю степень замещения или олигомеризации 
 находят по формуле (II-82).
находят по формуле (II-82).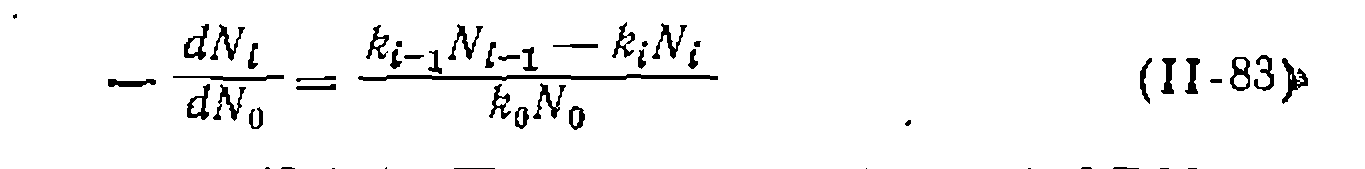
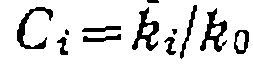 , используя их
, используя их , функция распределения описывается формулой Флори:
, функция распределения описывается формулой Флори:
 непрерывно уменьшаются от одной стадии к другой, то получится меньше низших и выс-
непрерывно уменьшаются от одной стадии к другой, то получится меньше низших и выс-
 мольные доли всех продук
мольные доли всех продук находим по разности:
находим по разности: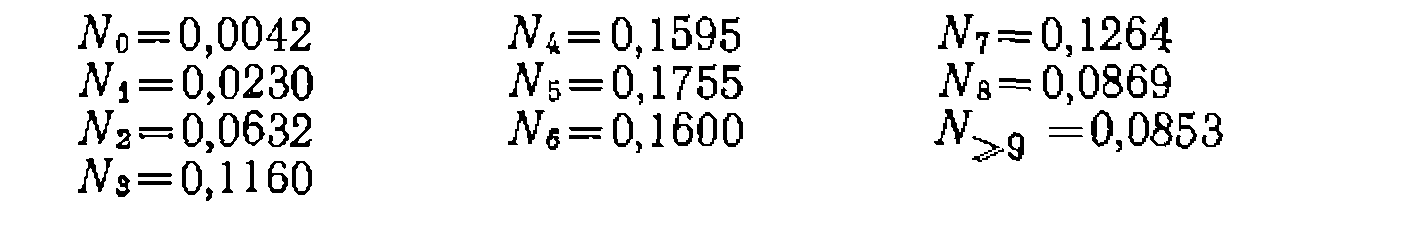
 , а следовательно, и средней степени олигоме
, а следовательно, и средней степени олигоме