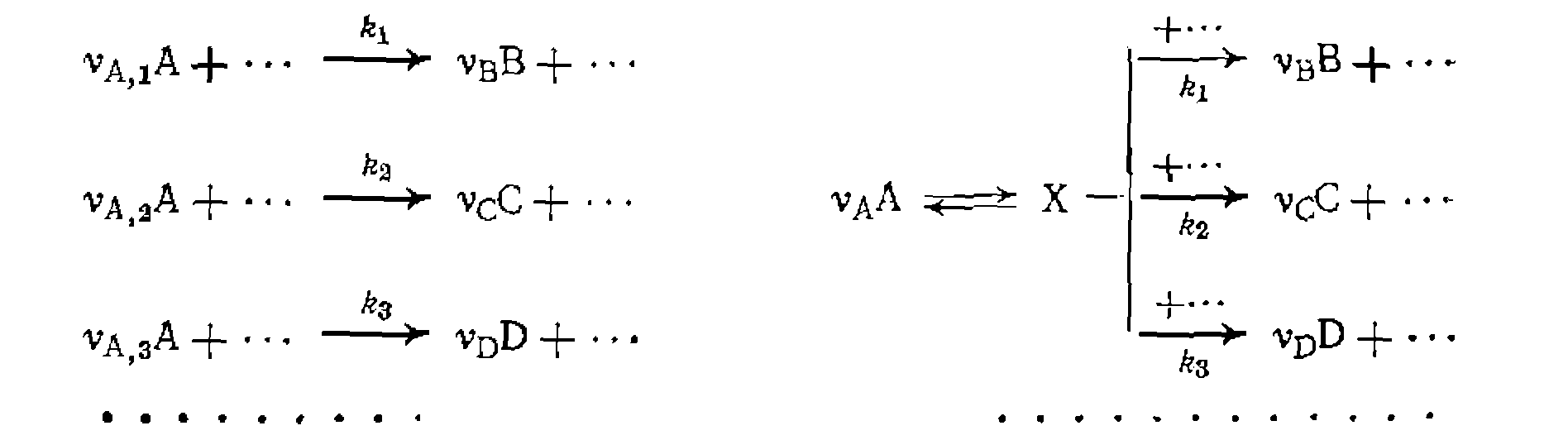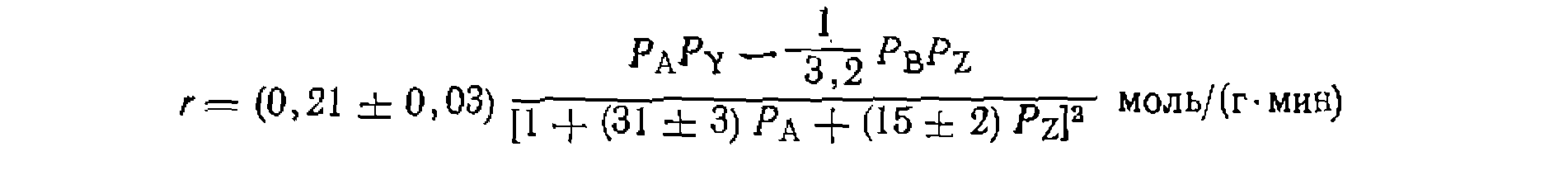|
|
Константы уравнения можно рассчитать но уравнениям линейного МНК или нрименить матричную форму расчета.дим из онытов левые части yi выведенного выше уравнения составляя матрицы функции и независимых переменных:
Транснонируем матрицу X н умножаем ее справа налево на матрицу Х> получая матрицу ошибок:
Умножаем далее Хт на матрицу Y н вычисляем матрицу
После этого находим значения констант уравнения:
Рассчитываем
сти уравнения онытиым данным. Для оценки доверительного интервала констаит составляем ковариациои* ную матоипу:
Следовательно
С учетом критерия Стьюдента н после исключения лишних значащих цифр получаем:
Коэффициент корреляции
Его величина соответствует высокой степени закоррелированности параметров. При расчете по нелинейному МНК. найдены несколько отличающиеся значения констант ходим обычным снособом
Чтобы найти доверительный интервал найденных коистант, вычисляем по интегоальной сЬпрме уравнения для каждой экспериментальной точки
имеющую п строк и два столбца. Из нее находим следующую ковариационную матрицу:
Квадратные корни нз диагональных элементов матрицы после их умножения «а /-критерии дают доверительные интервалы:
С их учетом получаем величину констант
и кинетическое уравнение
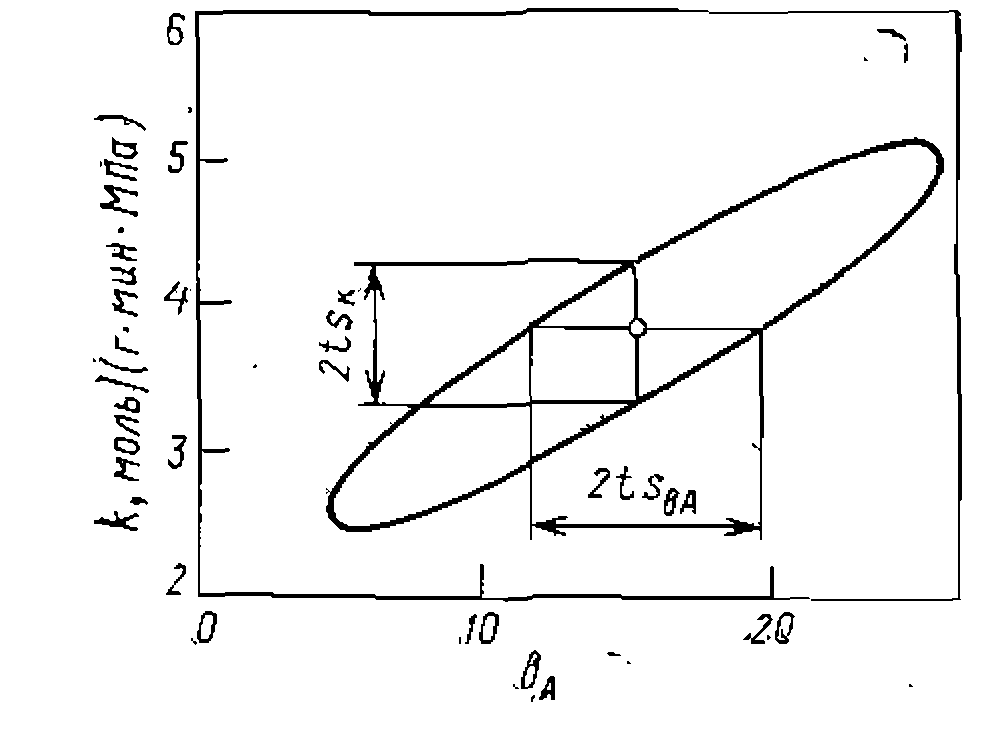
Для расчета по нелннейпому МНК на рис. 21 приведен вычисленный из опытов доверительный эллипс, внутри которого с 95%-й вероятностью на
ходятся истинные значения констант. Их можно было найти с меньшей стененью закоррелированности при увеличении числа опытов, особенно в области с повышенным парциальным давлением олефина (0,15—0,20МПа), поскольку оказалось, что обе серии опытов проводились прн
Рис. 21. Доверительный эллннс найденных констант уравнения. Аналогичным >образом, но в более сложной форме интегрируются кинетические уравнения -с тремя и -более членами в знаменателе. По ним можно обрабатывать опыты с помощью нелинейного МНК или, преобразовав в линеаризованную форму, по линейному МНК. Значительно сложнее интегрируются кинетические уравнения с многочленом в числителе. Они дают интегральные выражения, по которым поиск констант можно осуществлять только численными методами, т. е. на цифровых ЭВМ. Так, даже для обратимой реакции А^В с неизвестной константой равновесия получим:
где неизвестные помощью нелинейного МНК, приблизительно оценив кинетическая модель должна .быть .дополнена уравнениями баланса:
анз-за равновесных превращений образующихся солей
Часто еще более сложные аадачи возникают при обработке опытов по системе из одного уравнения скорости и сложных алгебраических уравнений балансов. Так, даже для элементарной реакции В результате интегральное решение уравнения скорости становится невозможным, и аадача поиска констант достигается методами численного интегрирования на цифровой ЭВМ. ДИФФЕРЕНЦИАЛЬНЫЙ МЕТОД ОБРАБОТКИ ОПЫТОВ ДЛЯ ПРОСТЫХ И ОБРАТИМЫХ РЕАКЦИИ ’Интегральный способ обработки эксперимента, как мы видели выше, часто приводит :к сложным выражениям, нередко решаемым лишь -численными методами. Этот -недостаток в значительной степени устраняется .'При дифференциальном способе, отличительной .особенностью которого 'является «обработка опытов непосредственно по дифференциальному кинетическому уравнению 1) дифференцированием кинетических кривых, полученных в периодических условиях 2) вычислением скоростей из экспериментальных данных, полученных в безградиентных условиях (аппарат полного смешения или проточно-циркуляционные установки). В первом случае дифференцирование проводят графически или численно в нескольких точках кинетических кривых, но это всегда связано с некоторыми дополнительными ошибками. Поэтому после установления адекватного опыту кинетического уравнения численные значения констант надежнее уточнять интегральным методом. Во втором случае скорости превращения веществ при варьируемых параметрах процесса вычисляют непосредственно из экспериментальных данных. Для этого служат выведенные ранее уравнения для реактора полного смешения [ (11-28), (И-29)^ (11-30)3, из которых при жидкофазных реакциях с постоянным объемом находим
В обоих случаях первичные опытные данные пересчитывают и сводят в таблицу, где для каждой точки дифференцирования кинетических кривых или для каждого опыта в безградиентных условиях сопоставляют текущие концентрации или парциальные- давления компонентов смеси и соответствующую им скорость превращения вещества. При этом парциальные давления для , простых и обратимых реакций вычисляют из степени конверсии с учетом коэффициента изменения объема во время реакции,
Последующая обработка опытов для уравнений с одной неизвестной константой может проводиться двумя способами. Если предполагается, что кинетика простой реакции описывается уравнением его логарифмируют и преобразуют в линейный многочлен можна линеаризация опытов на графике рительной оценкой значений уточнением при помощи МНК. Бели .при обработке опытов Второй способ .обработки .опытов для реакций с простым ти- 3IOM кинетического уравнения применяют для указанного выше уточнения константы скорости при округлении предварительно найденных порядков реакций .или для проверки выведенного из механизма уравнения скорости типа чаях значения г откладывают на графике против значений Оба способа обработки годятся и для обратимых реакций с .известной константой равновесия. При термодинамическом соответствии кинетики прямой и обратной реакций неизвестны только константа скорости и порядок прямой реакции, что позволяет преобразовать уравнение в логарифмическую форму, приведенную в табл. 12, где Когда в уравнении скорости содержатся две или более неизвестные константы, его также преобразуют в линейную форму. Так, для обратимой реакции с неизвестной константой равновесия и термодинамическим соответствием кинетики обеих реакций, описываемых уравнением
получим:
Из него с помощью МНК. находят Для кинетических уравнений., содержащих 'многочлен в знаменателе, преобразов авне в линейную 'форму достигается путем
их обращения. Например, для реакции, скорость которой описывается выражением
получим линейную форму
допускающую линеаризацию на плоскости. Из нее с помощью» МНК находят Линеаризованные формы некоторых кинетических уравнений для обработки опытов по дифференциальному методу приведены в табл. 12. Для газофазных реакций в эти уравнения вместо- При дифференциальном способе обработки опытов можно» применять и нелинейный МНК, принцип которого остается тем же, что и в интегральном способе, но используются более про* стые алгебраические уравнения. ROH + HC1 RCl+HaO ay в z > изучали в проточи о-цирку дявдонн ой. установке при постоянной температуре ни общем давлении 0,1 МПа, причем в некоторых опытах в исходную смесь добавляли продукты В или Z. Прн этом получены такие результаты:
Найти кинетическое уравнение н его константы, если /Ср?=3,2. Провести» статистическую обработку опытов с дискриминацией других возможных гипотез, имея в виду, что средняя квадратичная ошибка при четырех параллельных опытах равна При наиболее вероятном втором порядке прямой и обратной реакций: возможно несколько видов кинетического уравнения, прежде всего с первой’ и второй степенью знаменателя. Считая, что RC1 слабо адсорбируется поверхностью катализатора и его парциальное давление в знаменателе отсутствует^ обрабатываем опыты по таким двум линеаризованным формам уравнений?
CKODOCTH'. По линейным уравнениям ходим: Вариапт 1 Вариант 2
В обоих вариантах коэффициенты
Для оценки адекватности рассчитываем степени конверсии Вариант 1 Вариант 2
■что значительно больше дает. Аиалогичпо предыдущему рассчитываем для этих опытов парциальные давления и скорости
.тк/РА(0-10-\ г-мни/моль МПа . ХА..............................................
Оба ^-критерия оказались ниже табличных (8,94 и 9,03), что говорит об ■адекватности обоих уравнений. Для дискриминации одной из гипотез необходимы дополнительные опыты в области, где различие между ними будет <более существенным. Из анализа соответствующих уравнений видно, что в первом варианте адсорбционные коэффициенты настолько велики, что единица в знаменателе оказывается незначимой. Поэтому отличие от второго варианта снльнее проявится при низком парциальном давлении веществ А и Z. При общем давлении0,1 МПа этого можно достигнуть, проводя опыты при ^избытке НС1 и __ _ Кинетическому исследованию сложных реакций с двумя и более- независимыми переменными существенно помогает количественное определение соотношения образующихся продуктов и селективности реакции. Оно имеет значение и для изучения относительной реакционной способности веществ или разных положений молекулы.
Когда рассматриваются ключевые вещества, образующиеся по единственной необратимой параллельной реакции, получаем:
можно записать общее дифференциальное уравнение для соотношения количества образующихся продуктов:

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
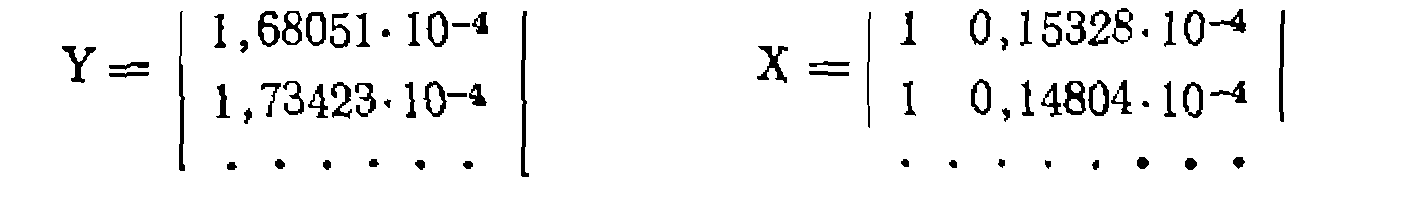
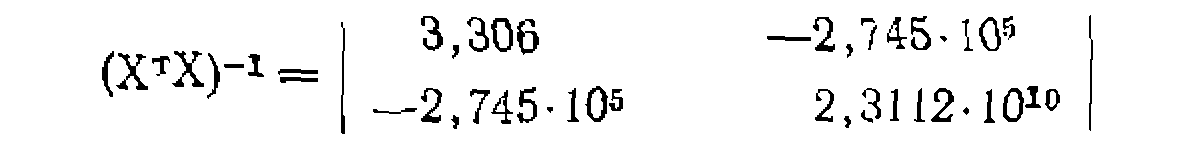
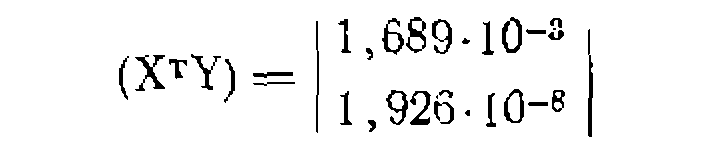
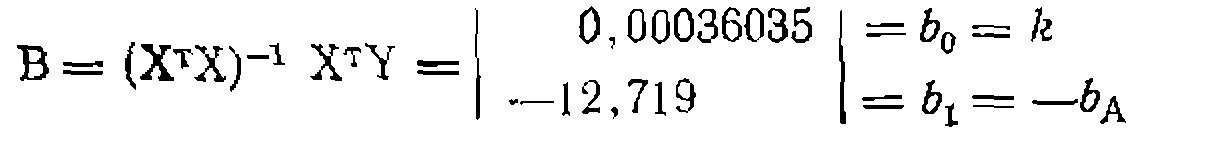
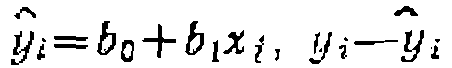 и дисперсию адекватности
и дисперсию адекватности 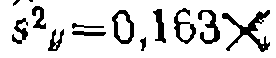
 . Для оценки дисперсии воспроизводим ости находим среднее отклонение в функции у при параллельных опытах, для чего дифференцируем ее:
. Для оценки дисперсии воспроизводим ости находим среднее отклонение в функции у при параллельных опытах, для чего дифференцируем ее: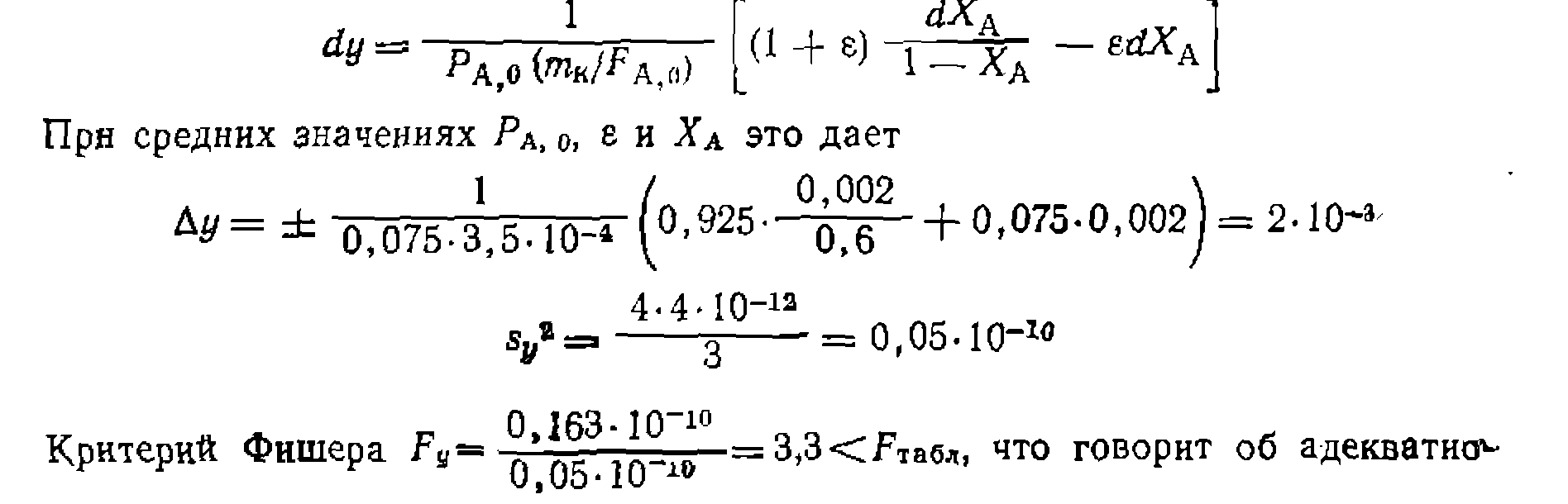
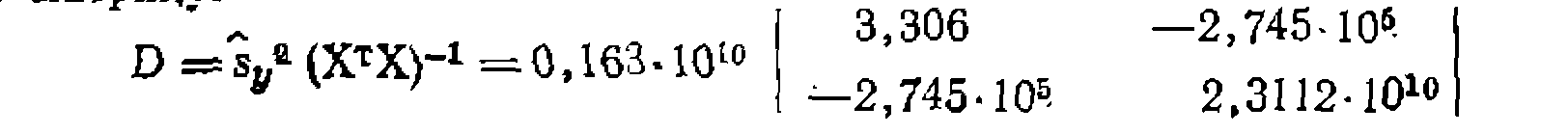
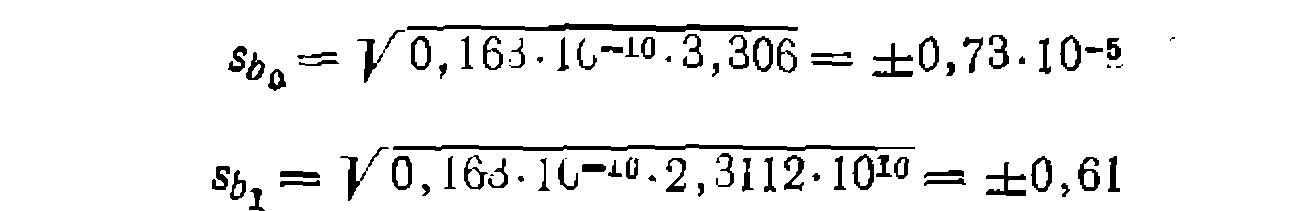
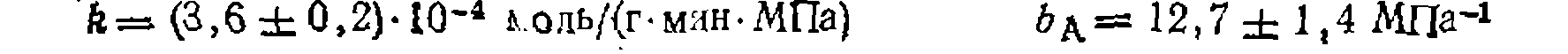
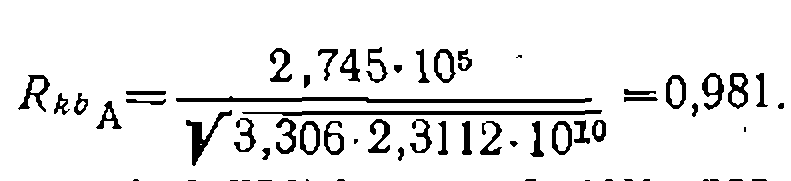
 . Для оцевки адекватности на
. Для оцевки адекватности на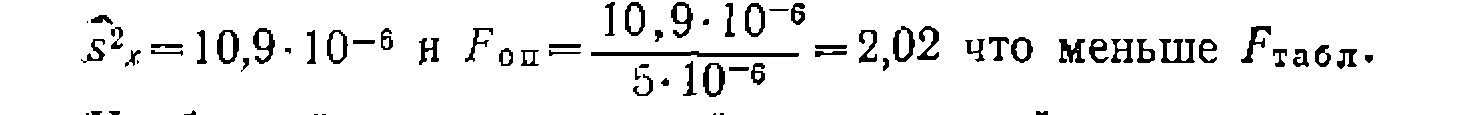
 нриннмая поочередное изменение
нриннмая поочередное изменение  и
и  соответственно на 0,3-10-4 н 0,1 по сравнению с их ранее найденным значением. В результате получаем матрицу
соответственно на 0,3-10-4 н 0,1 по сравнению с их ранее найденным значением. В результате получаем матрицу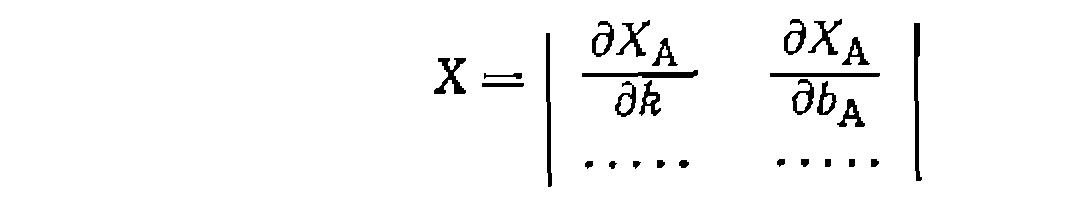
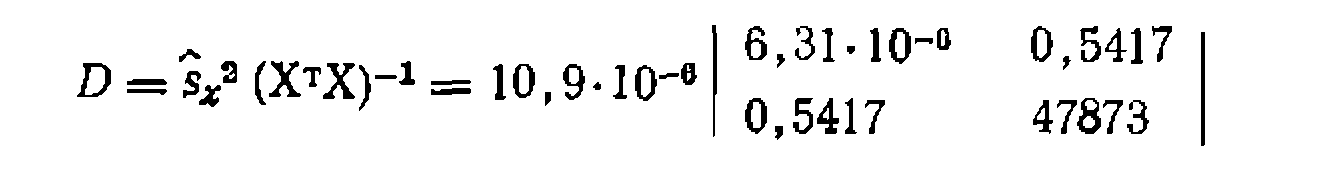
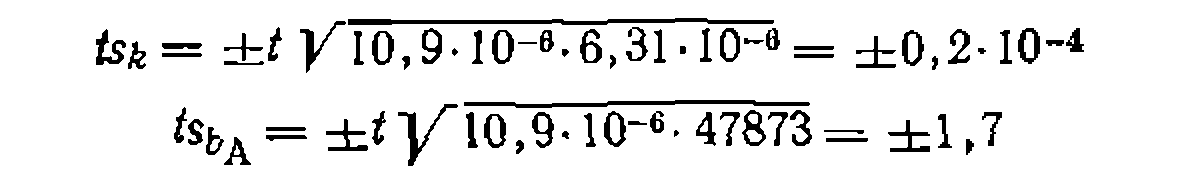
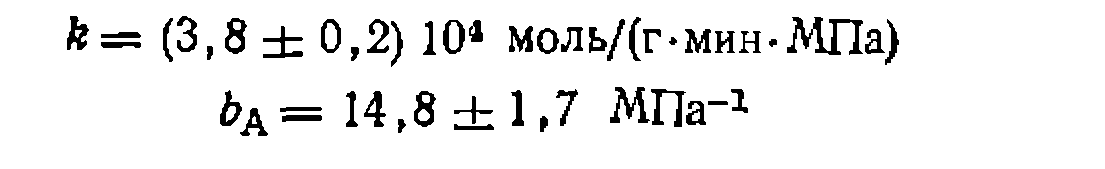
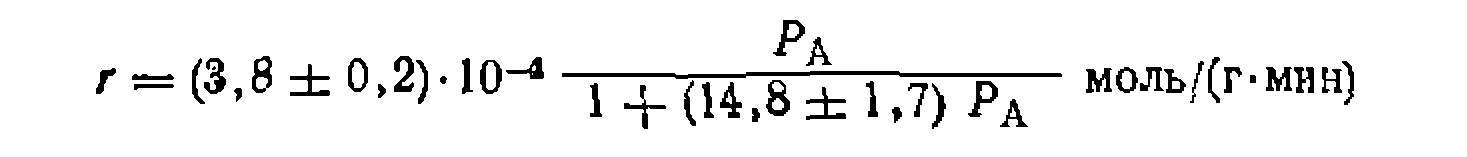
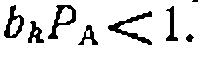
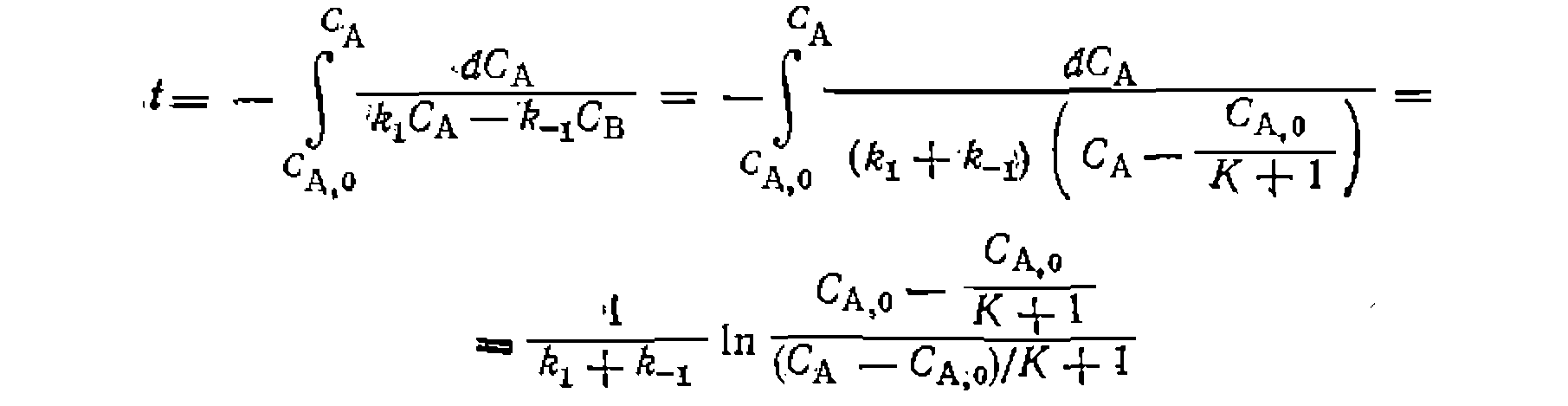
 и КтМ находят из опытных данных с
и КтМ находят из опытных данных с по начальным скоростям и К—из опытов при большом времени реакции.
по начальным скоростям и К—из опытов при большом времени реакции.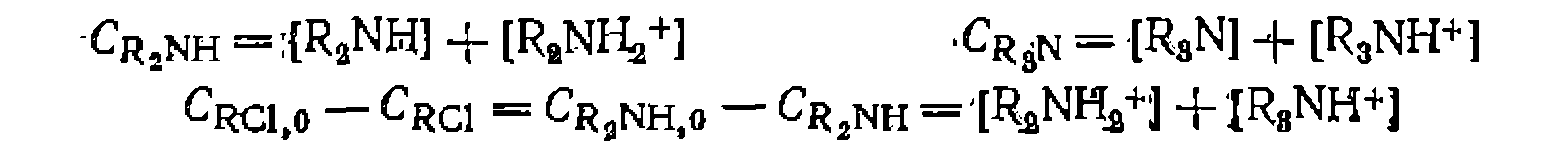
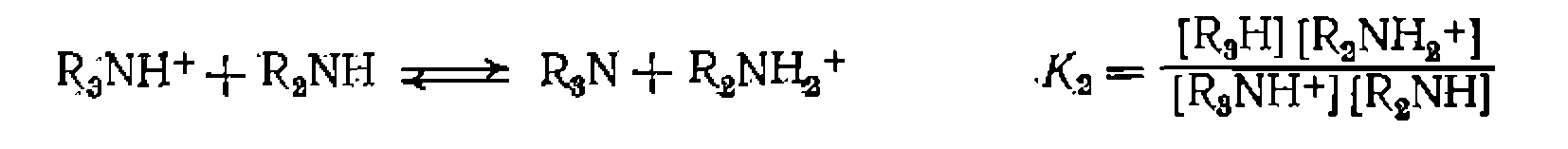
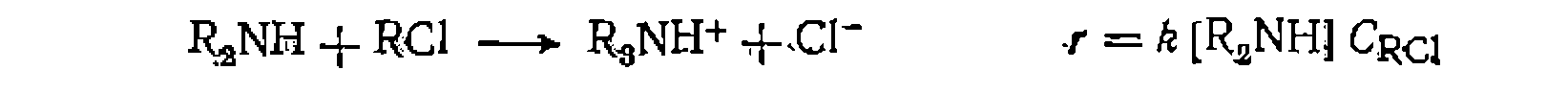
 без его интегрирования. При этом набор численных значений скорости при соответствующих значениях
без его интегрирования. При этом набор численных значений скорости при соответствующих значениях  можно получить двумя путями:
можно получить двумя путями: или в веактове идеального вытеснения
или в веактове идеального вытеснения  или
или 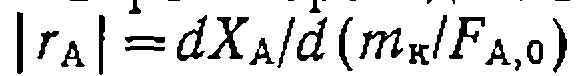 ;
;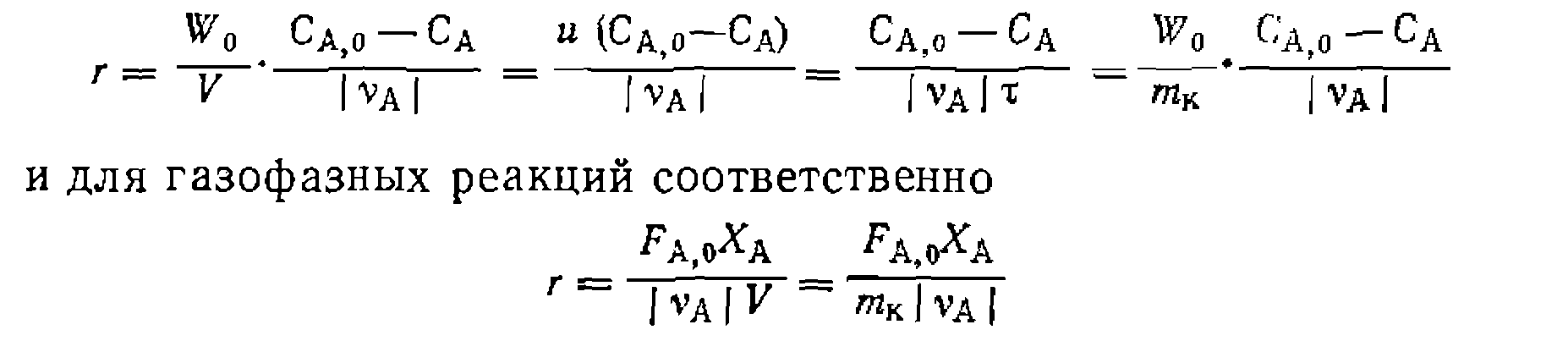
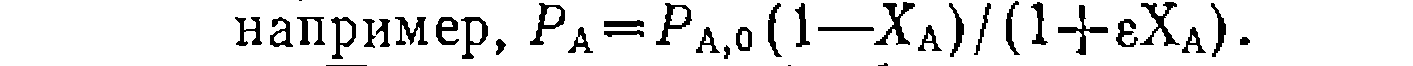
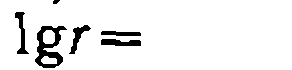
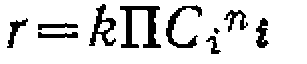 ? неизвестными порядками реакции, то
? неизвестными порядками реакции, то по которому линейным МНК находят
по которому линейным МНК находят  и
и 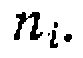 При наличии в правой части логарифмической формы уравнения только двух членов _
При наличии в правой части логарифмической формы уравнения только двух членов _ 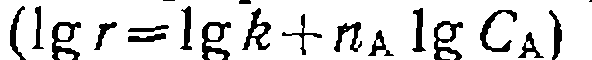 воз
воз с предва
с предва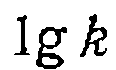 и
и  , но с последующим их
, но с последующим их получились близкими нулю, dzl или 2 (а для радикально-цепных реакций, кроме того, ±0,5 или 1,5)., их округляют до соответствующих величин и находят кинетическое уравнение, по которому значение константы уточняют излагаемым ниже способом. Нередко при подобной обработке эксперимента некоторые из значений
получились близкими нулю, dzl или 2 (а для радикально-цепных реакций, кроме того, ±0,5 или 1,5)., их округляют до соответствующих величин и находят кинетическое уравнение, по которому значение константы уточняют излагаемым ниже способом. Нередко при подобной обработке эксперимента некоторые из значений 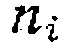 могут получиться существенно отличными от указанных выше (например, ОД 0,7 и т, д.). Такие порядки реакций назыв-ают кажущимися, а соответствующие им уравнения скорости обычно описывают процесс только в небольшом интервале варьирования параметров. Они ясно указывают, что реакция должна описываться другим уравнением, например, с многочленным знаменателем.
могут получиться существенно отличными от указанных выше (например, ОД 0,7 и т, д.). Такие порядки реакций назыв-ают кажущимися, а соответствующие им уравнения скорости обычно описывают процесс только в небольшом интервале варьирования параметров. Они ясно указывают, что реакция должна описываться другим уравнением, например, с многочленным знаменателем. „ В этих слу
„ В этих слу , и при правильности исходной гипотезы получают прямую, выходящую из начала координат, и находят
, и при правильности исходной гипотезы получают прямую, выходящую из начала координат, и находят 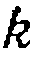 по.простейшему линейному уравнению _
по.простейшему линейному уравнению _ 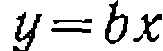
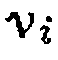 —стехиометрический коэффициент данного вещества с соответствующим знаком. В той же таблице приведено .и уравнение для обработки опытов при выведенном из механизма уравнении скорости.
—стехиометрический коэффициент данного вещества с соответствующим знаком. В той же таблице приведено .и уравнение для обработки опытов при выведенном из механизма уравнении скорости.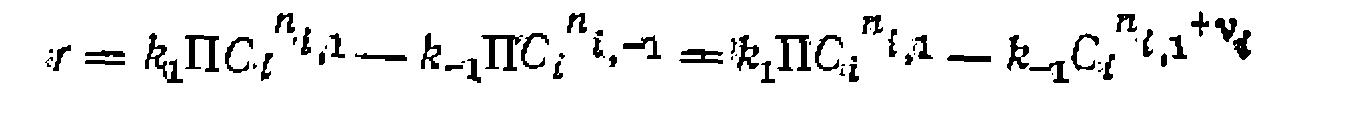
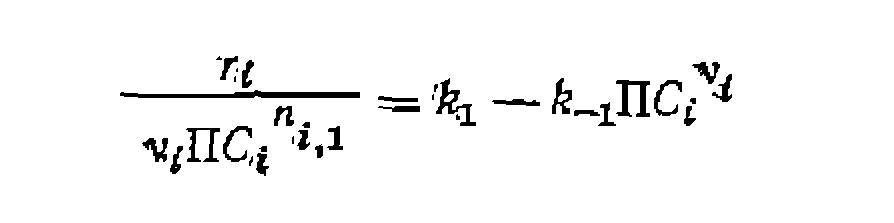
 и
и  , .а затем
, .а затем  Аналогично поступают с другими кинетическими уравнениями, ‘содержащими многочлен в числителе.
Аналогично поступают с другими кинетическими уравнениями, ‘содержащими многочлен в числителе.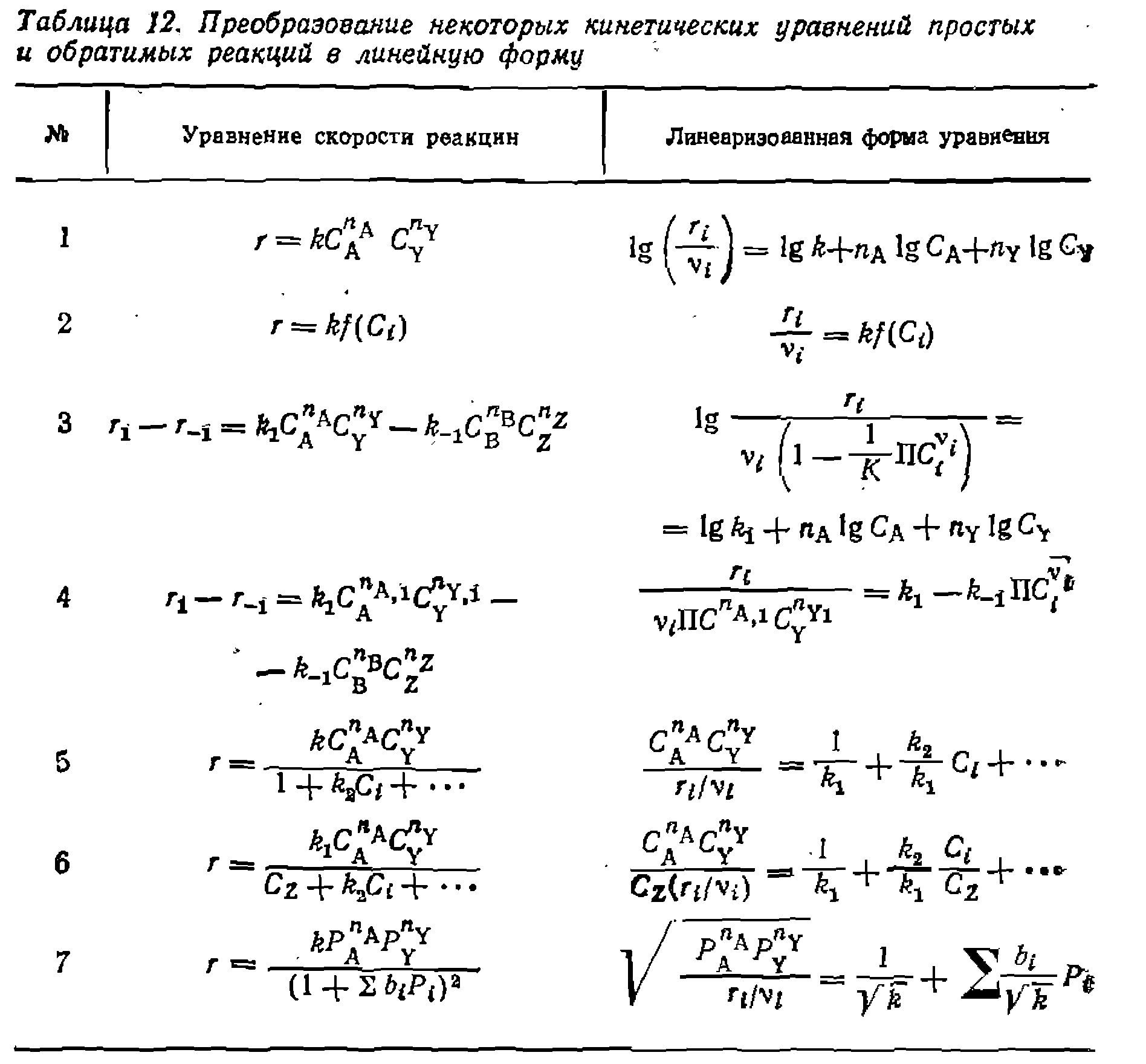
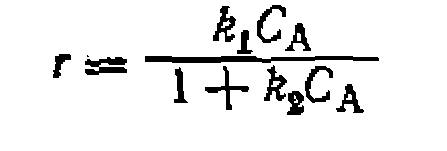
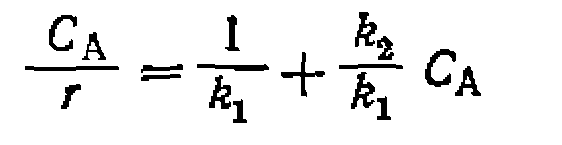
 и
и  , откуда определяют
, откуда определяют  и
и 
 подставляют
подставляют  , и наоборот.
, и наоборот.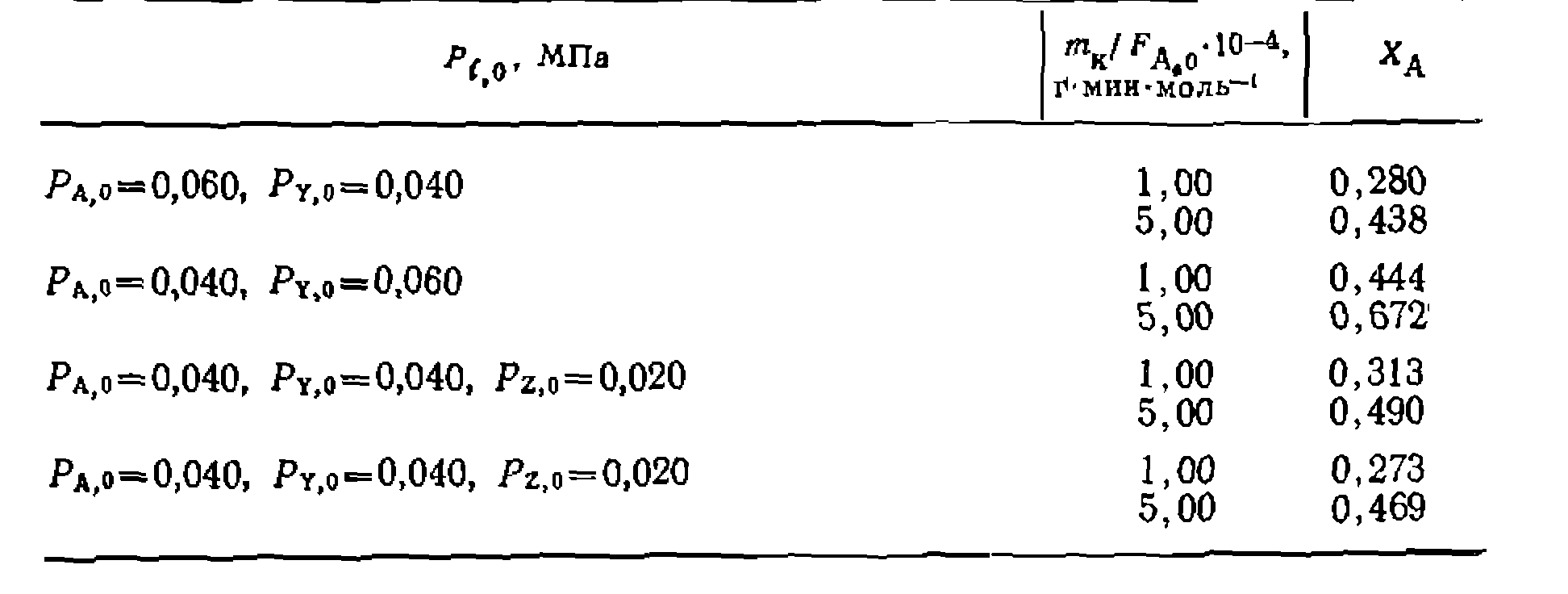
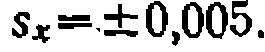
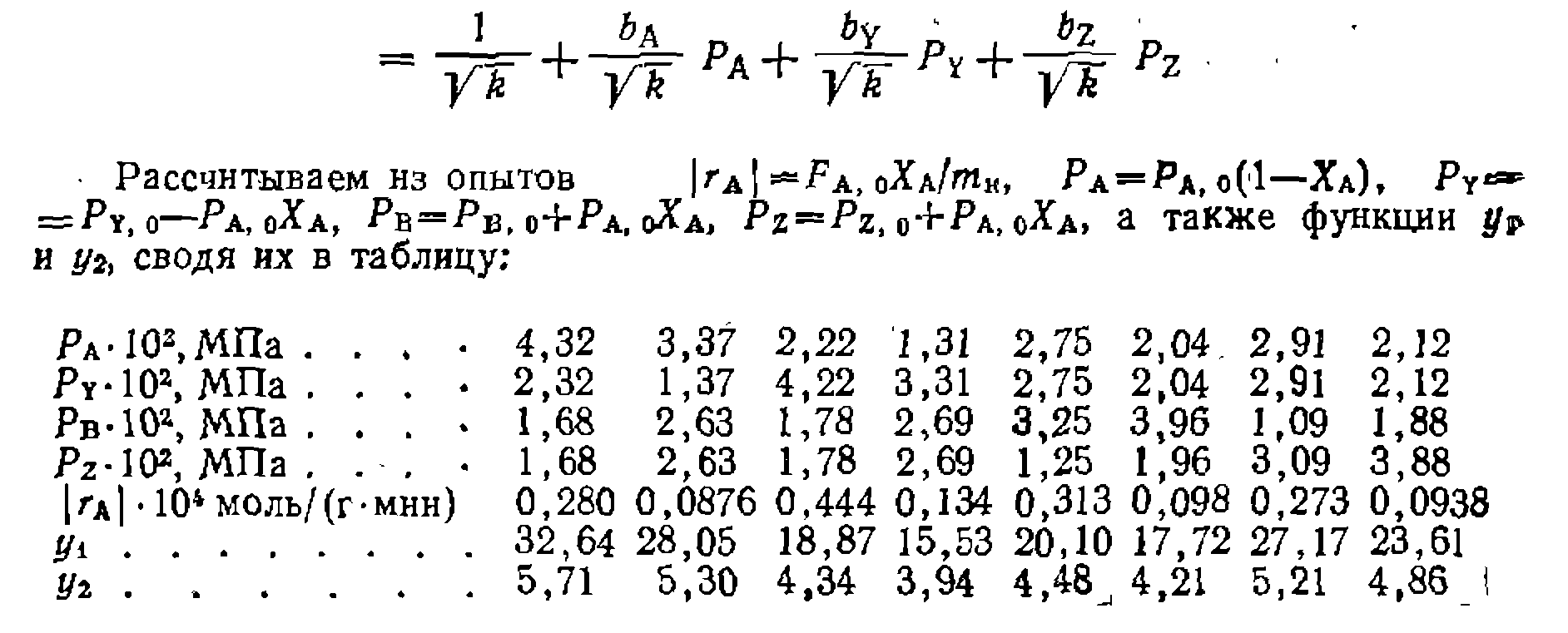
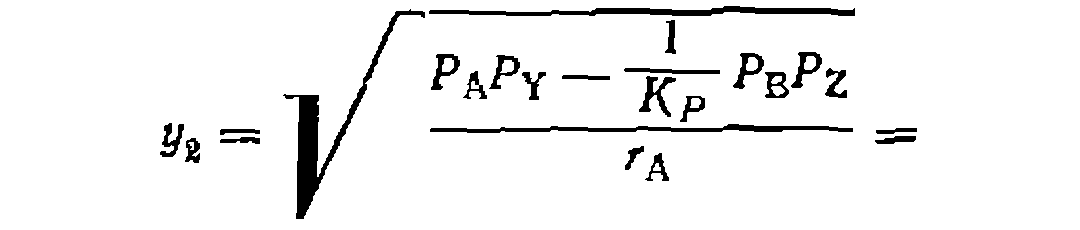
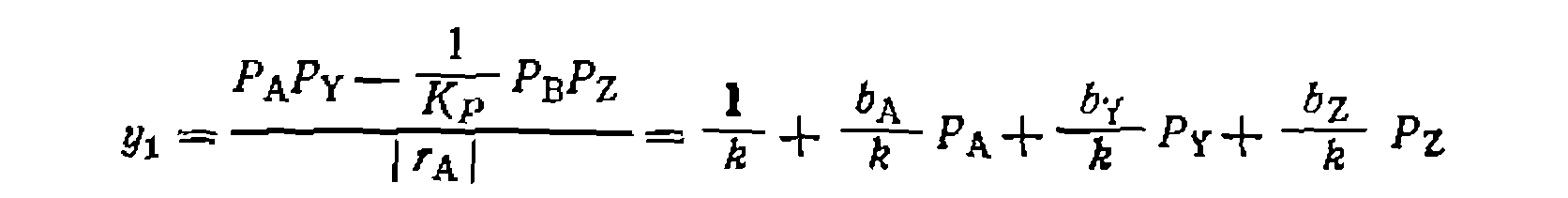
 с помощью МНК на
с помощью МНК на
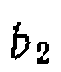 незиачимы, а в первом незначим и коэффициент
незиачимы, а в первом незначим и коэффициент  (это соответствует возможности пренебречь единицей в знаменателе кинетического уравнения). Исключая соответствующие члены, пересчитываем опыты и получаем:
(это соответствует возможности пренебречь единицей в знаменателе кинетического уравнения). Исключая соответствующие члены, пересчитываем опыты и получаем:
 , которые (Получатся при подстановке найденных коистант и параметров процесса в кинетические уравнения, дисперсию адекватности и критерии Фишера для обо- эдх вариантов:
, которые (Получатся при подстановке найденных коистант и параметров процесса в кинетические уравнения, дисперсию адекватности и критерии Фишера для обо- эдх вариантов: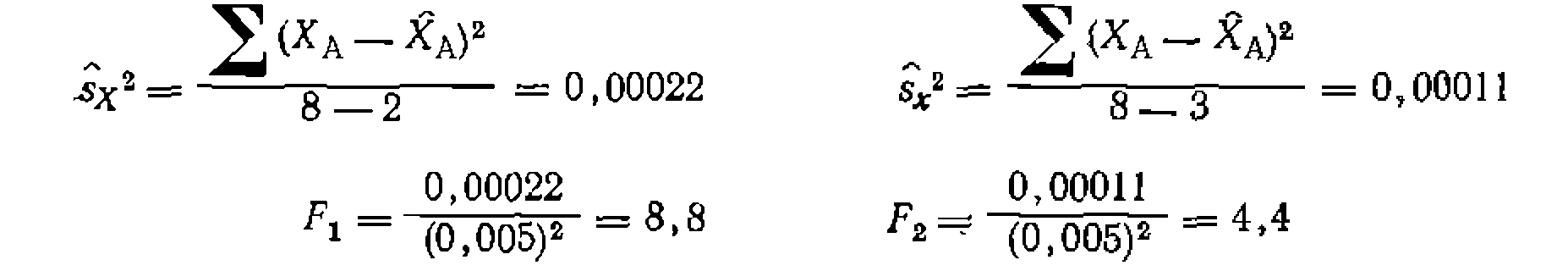
 . Следовательно, первая гипотеза отпа
. Следовательно, первая гипотеза отпа , после чего без пересчета найденных по первому варианту коистант находим
, после чего без пересчета найденных по первому варианту коистант находим  и остаточную сумму квадратов для четырех дополнительных опытов. Для первого варианта получаем
и остаточную сумму квадратов для четырех дополнительных опытов. Для первого варианта получаем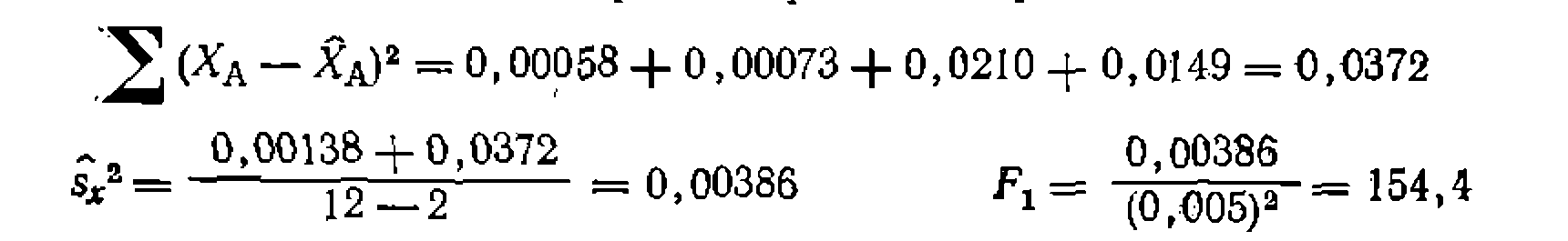
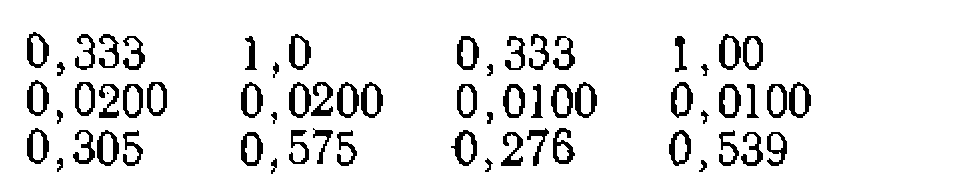
 __ _ . Они дали такие результаты:
__ _ . Они дали такие результаты: