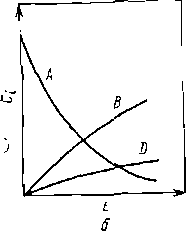МЕТОДИКА КИНЕТИЧЕСКОГО ИССЛЕДОВАНИЯ И ЭКСПЕРИМЕНТАЛЬНЫЕ УСТАНОВКИ

Кинетическому исследованию процесса всегда предшествует предварительный этап, о котором уже говорилось в начале этой главы. Обобщаются также литературные данные о механизме и кинетике изучаемых реакций.

Следующий, очень ответственный этап состоит в разработке экспериментальной установки и методики исследования, обеспе­чивающих достаточную точность и воспроизводимость опытов. Сюда входят выбор и проверка работы реакционного аппарата* регулирующих и измерительных приборов, способов анализа ре­акционной массы и т. д. Воспроизводимость, кроме того, зависит от качества и стабильности свойств применяемых реагентов, растворителей и катализаторов. Поэтому их качество и способы очистки надо обязательно охарактеризовать и поддерживать постоянными во время опытов. Полезно иметь какой-то базовый опыт и периодически повторять его, чтобы убедиться в воспро­изводимости получаемых данных.

где Ci,ср и Xi,ср — среднее арифметическое от найденных С* или Хи а пг— число параллельных опытов. Если параллельные опы­ты проводились при неодинаковых условиях, то дисперсию вос­производимости рассчитывают по уравнению

Воспроизводимость результатов процесса, т. е. найденных: экспериментально концентраций веществ Сi или их выходов (xi), оценивают, ставя параллельные опыты, по так называемой дисперсии воспроизводимости. Если все параллельные опыты проведены при одних и тех же условиях, дисперсию воспроизво­димости находят по уравнению

концентраций или выходов, а двойное суммирование квадратов отклонений проводится для каждой серии параллельных опы­тов в зависимости от значений Сi_{; ср} или xi,_ср.

Пример 1. Рассчитать дисперсию воспроизводимости для пяти парал­лельных опытов, при которых найдены концентрации вещества в реакцион­ной смеси, равные 0,126, 0,121, 0,122, 0,119 и 0,122 моль/л. Находим Сср и .дисперсию воспроизводимости sг:

Пример 2. Рассчитать дисперсию воспроизводимости выходов вещества для следующих параллельных опытов, проводимых при четырех разных условиях процесса:

Находим:

где слагаемые в числителе сгруппированы по величине отклонений от средне­го в каждой серии опытов.

Само кинетическое исследование основано на том, что экс­периментально определяемые результаты (Сi, Xi)зависят от дифференциальных уравнений скорости реакций и от парамет­ров процесса. Чтобы, найти кинетические уравнения, необходи­мо варьировать все параметры, которые могут влиять на ско­рость: начальные концентрации (парциальные давления) всех реагентов (а нередко и продуктов реакции, которые могут ее автокатализировать или тормозить), концентрацию катализато­ра, температуру, а также временные характеристики процесса (длительность реакции или так называемое условное время кон­такта). Обычно наиболее сложной задачей является нахожде­ние концентрационной формы уравнений скорости (II-I3). Она упрощается, если каждый опыт проводится в изотермических условиях, когда параметры 0jпостоянны. С этой же целью ти­пична постановка в первую очередь большой серии опытов при одной, предварительно подобранной температуре, но с варьиро­ванием всех остальных параметров. Найдя по этим данным ки­нетические уравнения и проведя уже меньшее число опытов при двух-четырех других температурах, находят зависимость пара­метров реакции (0j) от температуры по уравнениям типа урав­нений Аррениуса.

При варьировании параметров часто применяют так назы­ваемый однофакторный эксперимент, когда в сериях опытов из­меняют попеременно только один параметр при постоянстве

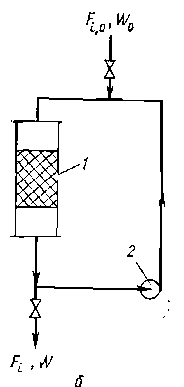
Рис. 5. Схема (а) и концентрационные кривые (б) идеального периодического реактора.

остальных. В более простых случаях для сокращения числа опытов можно использовать и многофакторный эксперимент, когда сразу варьируют два или более параметра.

Поиск кинетических уравнений упрощается при изучении процесса в реакционных аппаратах, обеспечивающих наиболее простую связь между результатами процесса и варьируемыми 'параметрами. К таким аппаратам относятся реакторы с идеаль­ным режимом (структурой) потока реакционной смеси: реакто­ры идеального или полного смешения (периодический и непре­рывный) и реакторы идеального вытеснения (непрерывный). Для сокращения мы будем называть их в дальнейшем идеаль­ными реакторами (периодическим, вытеснения и смешения).

Идеальный периодический реактор и исследование кинетики в периодических условиях. Условием идеальности периодическо­го реактора (рис. 5, а) является отсутствие градиента концент­раций и температур по его объему (dCi/dV=dT/dV=0), что возможно лишь при достаточно интенсивном перемешивании. Кроме того, предполагается мгновенная загрузка компонентов смеси или, во- всяком случае;, последнего из них, при добавлении которого сразу начинается реакция и фиксируется ее нулевое время.

В периодическом реакторе концентрации веществ изменяют­ся только во времени (рис. 5,6), а в каждый данный момент концентрации и скорости постоянны по его объему. Это позво­ляет составить материальный баланс по любому веществу за бесконечно малый промежуток времени (dni=Vridt) и полу­чить после интегрирования от 0 до t,когда количество вещества изменяется от ni,₀ до пi, следующее общее уравнение идеально­го периодического реактора:

Здесьmx/V—массакатализатора в единице объема смеси за вычетом объема, занимаемого катализатором. Ее часто (но не совсем точно) называют концентрацией катализатора.

Бели реакционный объем остается постоянным, то dfii=VdCi, что дает концентрационную форму уравнения:

В случае гетерогенно-каталитической реакции из дифферен­циального уравнения баланса (dni = mxridi) получаем

и при постоянстве объема во время реакции имеем следующую концентрационную форму уравнения:

Выведенные уравнения показывают, что в периодических условиях экспериментально определяемым результатом процес­са являются так называемые текущие концентрации веществ C_irа варьировать приходится, кроме начальных концентраций всех веществ и температуры )[они влияют на вид уравнений (II-17) — (II-20) в скрытой форме через ri], временем реакции, а для ге­терогенно-каталитических процессов — величиной mk/V.

Периодические условия используют преимущественно для кинетического исследования жидкофазных реакций. Реактором» как правило, служит колба или автоклав с мешалкой, помеща­емые в термостат, с помощью которого поддерживается нужная температура (обычно с точностью ±0,1/0,2°С). Аппарат снаб­жен устройствами для загрузки компонентов смеси (воронка­ми), термометром и, если нужно, обратным холодильником и пробоотборником. Чаще всего после начала реакции в точно фиксированное по секундомеру время отбирают пробы реакци­онной массы, тем или иным способом быстро прекращают в них реакцию и анализируют состав (титрованием, спектральным или хроматографическим методом). При этом в смеси необходимо определять по меньшей мере столько же ключевых веществ, сколько в данной системе имеется независимых реакций. Суще­ствуют н способы наблюдения за ходом реакции без отбора проб, например по давлению паров, по изменению объема, цир­куляцией жидкости через специальную ячейку, где снимаются спектральные данные, и т. д. Поэтому периодические условия

изучения кинетики наименее трудоемки — за один опыт полу­чают ряд экспериментальных точек при разном времени реак­ции. Результаты сводят в таблицу экспериментов, где сопостав­ляются варьируемые параметры и найденные текущие концент­рации веществ. Нередко их изображают также графически в виде кинетических кривых в координатах Сt—t(см. рис. 5, б).

Реактор идеального вытеснения и кинетическое изучение процесса в потоке. Реактор идеального вытеснения (рис. 6, а) является идеализированной моделью непрерывно действующих аппаратов вытеснения, в которых реакционная масса движется вдоль оси, «вытесняя» последующие слои. Условие его идеаль­ности состоит в том, что каждый элемент потока в данном по­перечном сечении аппарата движется вдоль оси с одинаковой линейной скоростью (поршневой режим). Это предполагает от­сутствие торможения потока стенками или насадкой, а также отсутствие диффузионных явлений, из которых наиболее значи­тельно продольное (или обратное) перемешивание. При стацио­нарном режиме работы, т. е. при постоянстве скорости подачи и состава исходной смеси, а также условий теплообмена, каж­дый элемент потока пребывает в таком реакторе в течение оди­накового времени, а концентрации и температура в каждом по­перечном сечении остаются постоянными. При этом в отличие от периодического реактора концентрации веществ изменяются не во времени, а по длине аппарата (рис. 6,6). Это позволяет составить уравнение материального баланса для бесконечно ма­лого элемента объема, поперечного потоку реагентов (dFi =ridV), и после интегрирования от 0 до V, когда мольный по­ток любого из веществ меняется от Fi,₀до Fi,получить общее уравнение:

Если на рис. 6, aWoпредставляет собой объемный поток всей реакционной смеси (объем/время), приведенной к темпера­туре и давлению в реакторе, то при постоянстве объема смеси во время реакции имеем Fi = WoCiи dFi = WodCi, что позволяет

получить концентрационную форму уравнения;

В нем V/Woимеет размерность времени и при отсутствии насад­ки в реакторе или за вычетом ее объема равно истинному времени контакта. Очевидно, что в этом случае уравнения (II-18) для периодического реактора и (11-22) полностью совпадают.

Более общую форму уравнения для реактора идеального вытеснения, верную и для меняющегося объема смеси, можно вывести, заменяя Ftчерез выходы ключевых веществ (Fi= v'i/|v'a|Fa,oxi;^a) :

Это уравнение годится и для основного реагента А, если пола­гать, что его выход равен хA=1-XA. В левой части уравнения (II-23) находится величина, обратная мольной нагрузке едини­цы объема реактора по основному реагенту в единицу времени Fa.o/Vи имеющая размерность

[ (объем) (время) (моль)^-1]. Она называется условным временем контакта и является временной характеристикой гомогенных непрерывных процессов, заменяю* щей время реакции при периодических условиях. ,

Для гетерогеннокаталитических реакций материальный ба­ланс можно составить не для микрообъема, а для микромассы катализатора (dFi = ridm_K)и соответственно предыдущему по­лучить:

Чаще используют последнее уравнение, в левой части которого находится величина, обратная мольной нагрузке единицы мас­сы катализатора по основному реагенту в единицу времени — FA,o/mk и имеющая размерность [(масса) (время) (моль)^-1];

Ее также называют условным временем контакта, и она является временной характеристикой непрерывных гетерогенно-ката­литических реакций.

Иногда (особенно в технологии) используют еще одну вре­менную характеристику процесса, а именно объемную скорость и;[ (время)^-1]. Если ее выражать по объему всей поступающей смеси, приведенному к условиям в реакторе, то u — Wo/V, т. е. объемная скорость равна объемной нагрузке единицы реакцион­ного объема в единицу времени. Тогда при неизменности объ­ема смеси во время реакции и = т^-1ист. Объемную скорость при­меняют и для характеристики гетерогенно-каталитических про­цессов, относя ее к насыпной массе катализатора. Кроме того, ее часто выражают по объемному потоку не всей смеси, а только основного реагента, и притом в нормальных условиях (0,102 МПа и 20 °С). Чтобы использовать такие величины в пре­дыдущих уравнениях, их надо пересчитывать на условное время контакта.

Реакторы.идеального вытеснения применяют для кинетиче­ского исследования реакций в потоке, особенно для газофазных процессов, в том числе гетерогенно-каталитических. К условиям идеального вытеснения близки аппараты большой длины и ма­лого диаметра при турбулентном движении газа. Поэтому реак­тор изготавливают в виде трубки (которую можно заполнять катализатором) или змеевика, имеющих карманы для термо­пар. Газообразные вещества подают в аппарат из баллонов или газометров, точно регулируя и изменяя скорость их потока. Жидкие вещества вводят при помощи микронасосов или градуи­рованных дозаторов разного типа. Все компоненты смешивают и предварительно испаряют или подогревают до температуры реакции (прежде чем подать в реактор). Поскольку теплопере­дача от газа к стенке малоинтенсивна, особенно при наличии ге­терогенного катализатора, больше значения имеет организация теплообмена., гарантирующая постоянство температуры по длине диаметру реактора. Этого достигают, помещая реактор в термостат или баню с псевдоожиженным слоем песка, а также при помощи электрообогрева. Для реакций с большим выделе­нием или поглощением тепла целесообразно применять трубки малого диаметра, разбавлять гетерогенный катализатор инерт­ной насадкой и т. д. Ввиду трудностей с теплообменом в этом типе реактора допускается регулирование температуры с пони­женной точностью —до +1—2°С.

Перед началом каждого опыта через реактор надо пропус­тить 3—5 объемов смеси заданного состава, чтобы в аппарате установился стационарный режим. После этого накапливают пробу продуктов и анализируют ее тем или иным методом, на­чиная следующий опыт при других параметрах процесса. Сле­довательно, каждый опыт дает только одну экспериментальную точку, обусловливая большую длительность и трудоемкость ис­следования по сравнению с периодическими условиями. При

Рис. 7. Схема (о) и концентрационные прямые (б) реактора полного сме­шения.

этом варьируют те -же параметры, но вместо времени изменяют условное время контакта (V/FА,о или mк/F_A,o).

Экспериментальные данные сводят в таблицы; если нужно, представляют их в виде кинетических кривых в координатах Xi^A—V/F_A,оили mк/F_A,о(рис. 6,6). Эти же таблицы и графики могут содержать и вычисленные из опытов данные о селектив­ности.

Реактор полного смешения и кинетическое исследование процесса в безградиентных условиях. Реактор полного смеше­ния (рис. 7,а) также является непрерывно действующим. Усло­вие его идеальности состоит ,в отсутствии градиента концентра­ций и температуры по объему (dCi/dV=dT/dV=0), причем в стационарных условиях этот градиент отсутствует и во време­ни. При введении исходной смеси в большой реакционный объ­ем происходит скачкообразное снижение концентраций реаген­тов до величины, равной концентрации в реакторе и на выходе из аппарата (рис. 7,6). Для стационарных условий работы по изложенным причинам можно составить баланс для реактора в целом (Fi— Fi,o = riVили rimk), откуда получаем общее урав­нение:

При постоянстве объема смеси во время реакции справедли­во равенство

Fi= WoCi,откуда имеем концентрационные формы уравнений:

применимые не только при W=const, но и при переменном объ­еме смеси:

В этих уравнениях величины х, и, V/F_A)qи mk/F_A,о имеют тот же •смысл и наименования, как и для реакторов идеального вытес­нения.

В реакторах периодического действия и идеального вытесне­ния концентрации изменяются во времени или по объему, и конечный результат находят после интегрирования (интегральные реакторы). В отличие от этого, в аппарате полного смешения градиент концентраций отсутствует (безградиентные условия процесса), а конечный результат находят, решая алгебраиче­ское уравнение, что значительно упрощает расчет.

Безградиентные условия применяют для кинетического изу­чения главным образом газофазных (в том числе гетерогенно­каталитических) реакций. Реактор может быть устроен по типу изображенному на рис. 7, а; он до лжен иметь хорошо действую­щую мешалку, на которой может находиться и помещенный вметаллическую сетку гетерогенный катализатор. Относительно редко применяют так называемый дифференциальный реактор (рис. 8, а). Он близок к модели идеального вытеснения, но ис­следование ведут при малой степени конверсии, когда можно пренебречь изменением концентраций. Недостаток такого аппа­рата состоит в малой точности результатов, так как небольшая разность C_i,0—Ciопределяется со значительной погрешностью Пожалуй, наибольшее применение нашли так называемые про­
точно-циркуляционные установки, в которых осуществляется циркуляция реакционной смеси через реакционное пространство¹ (катализатор). При высокой степени циркуляции такие установ­ки близки к реактору-полного смешения. В одних (рис. 8,6) ор­ганизована внешняя циркуляция при помощи газодувки или компрессора, в других (рис. 8, в) имеется внутренняя циркуля­ция при помощи поршня, который через систему клапанов осу­ществляет смешение реакционной массы и ее проталкивание че­рез слой катализатора.

Остальное оснащение безградиентных установок и последо­вательность проведения опытов — такие же, как для реакций в потоке. Очень важно, что температурный режим в них регули­руется проще и точнее, а результаты исследования газофазных гетерогенно-каталитических реакций в безградиентных условиях считаются самыми достоверными.

Не нашли, что искали? Воспользуйтесь поиском по сайту: