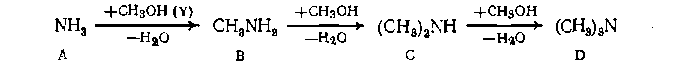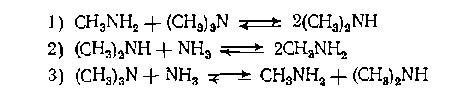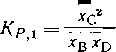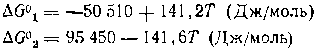|
|
КОНСТАНТЫ РАВНОВЕСИЯ ЖИДКОФАЗНЫХ РЕАКЦИЙТермодинамические расчеты обратимых реакций, протекающих в жидкой фазе или в гетерофазных системах, несколько отличаются от расчетов для газофазных реакций, поскольку приходится учитывать физико-химические особенности жидкого состояния вещества и растворов. Использование понятия активности позволяет и в этом случае упростить решение многих задач, хотя на этом пути могут встретиться значительные трудности. В идеальных растворах, подчиняющихся законам Рауля и Генри, летучесть компонентов пропорциональна нх мольной доле в растворе и при небольших давлениях практически не отличается от парциального давления соответствующих компонентов над раствором
где Ni— мольная доля вещества iв растворе, Р,:,р-p и Р;; ж — парциальное давление над раствором и давление насыщенного Бара чистой жидкости для iкомпонента. Если рассматривать идеальный раствор как смесь компонентов, не выделяя растворитель и растворенные вещества, то стандартными следует считать состояния каждого компонента в виде чистой жидкости, когда его стандартная летучесть равна f°i,ж. Отсюда следует, что активности компонентов таких растворов совпадают с мольными долями
Для расчета равновесии таких идеальных систем можно использовать данные об энергиях Гиббса образования каждого- компонента из простых веществ для стандартного газообразного состояния ∆G0f, г. Для этого из них рассчитывают энергию- Гиббса для стандартного состояния чистой жидкости ∆G0i,ж, которая равна сумме ∆G0f, г и энергии перевода вещества из состояния насыщенного пара в стандартное газовое состояние (испарение не сопровождается изменением ∆G0)
Следовательно, для расчета равновесия жидкофазной реакции можно рассмотренным ранее образом определить Кр и затем с учетом давления насыщенного пара над чистыми компонентами реакции рассчитать Kn Такой способ расчета дает удовлетворительные результаты для превращений углеводородов и галогенпроизводных; в меньшей степени он пригоден для органических соединений других классов. Так, дляизомеризация н-бутана в изобутан стандартное изменение энергии Гиббса для газообразного состояния равно ∆G298=—3767 Дж/моль, что дает константу равновесия для газовой фазы, равную:
Давления насыщенных паров чистых н-бутана и изобутана при 298 К равны соответственно 2,40 и 3,43 ат. Отсюда константа равновесия той же реакции в жидкой фазе равна:
Из рассмотренного примера и уравнения (1-19) видно, что при образовании более летучих веществ из менее летучих константа равновесия в жидкой фазе меньше, чем в газовой. Другим примером этого является реакция этерификации уксусной кислоты этанолом СНзСООН+С2Н5ОН=СНзСООС2Н5+Н20, для которой, несмотря на неидеальность системы, наблюдается та же зависимость: в жидкой фазе константа равновесия равна Рис. 2. Обработка экспериментальных дшшых по зависимости парциального дп пления паров вещества от его мольной доли в растворе.
примерно 4, а в газовой фазе достигает 15—20. Противоположный пример — реакция синтеза метанола СО + 2Н2= СНзОН, когда образуется менее летучее вещество и константа равновесия жидкофазной реакции значительно больше, чем для газофазной- Рассмотренный метод оказывается непригодным для растворов, отклоняющихся от законов Рауля и Генри; к таким растворам относится большинство систем, представляющих практический интерес. Согласно теории активностей, в этих условиях необходимо знать термодинамические характеристики растворенных веществ в стандартном состоянии, которым считается их состояние в идеальных растворах с активностью, равной единице. Для описания этого (обычно фиктивного') состояния требуются экспериментальные данные об изменении парциального давления компонента над раствором в зависимости от его мольной доли в области очень разбавленных растворов, когда безразмерную активность вещества в газовой фазе можно приравнять его парциальному давлению в атмосферах;
где Ki— константа фазового равновесия i-roкомпонента. При бесконечном разбавлении все растворы близки к идеальным; тогда, согласно уравнению (1-17)
и, следовательно, имеем:
В области очень разбавленных растворов зависимость последней должна стремиться к константе фазового равновесия К-i,которая будет определяться величиной отрезка, отсекаемого на оси ординат в указанных координатах (рис. 2). Обычно такая зависимость вблизи нуля становится линейной, что позволяет провести экстраполяцию к нулю. Из найденного значения Kiрассчитывают парциальное давление пара компонента iнад раствором, где его активность а;, р-р равна 1:
Как и по уравнению (1-18), теперь оказывается возможным оценить энергию Гиббса образования компонента iпри его стандартном состоянии в растворе:
К сожалению, изложенные выше приемы нахождения константы равновесия в жидкой фазе по данным о стандартных энергиях Гиббса образования реагентов являются скорее иллюстрацией, чем руководством к расчету. Теоретически они справедливы и применимы для случаев, когда растворенные вещества сольватируются растворителем и не оказывают влияния друг на друга, так как иначе константа фазового равновесия компонента становится функцией состава смеси и зависит от содержания других веществ в растворе, т. е. уравнения делаются неприменимыми.
В заключение рассмотрим равновесие гетерофазных реакций, протекающих в жидкой фазе, но с участием не только жидких, но и газообразных веществ, в тон или иной мере растворимых в жидкой фазе (гидрирование водородом, отщепление НС1 и др.). Для них константа равновесия жидкофазной реакции причем активность газообразных веществ в растворе аi,p-p=Kiaiг. Константы распределения Кi. можно ввести в константу равновесия и пользоваться другой ее величиной Ka= П(avip.pavi, г), где активность жидких и; газообразных веществ относится соответственно' к той фазе„ где эти компоненты преимущественно находятся. Тогда для для жидкофазного гидрирования бензола в циклогексаа имеем;
Последнее означает, что для веществ, находящихся в жидкой фазе, за стандартное принято состояние чистой жидкости, а для газа—состояние идеального газа при давлении 1 ат (0,1013 МПа). Очевидно, что для неидеальных систем за стандартное надо принимать идеальное состояние с ai =1. Методы расчета ∆G0f,p.pи ∆G°f,r, а также ∆G° = —RTlnKдля неидеального газа и раствора уже были рассмотрены, причем они справедливы и для гетерофазных реакций с теми же ограничениями, которые указаны ранее. Иногда точные данные по термодинамическим функциям или равновесию реакций отсутствуют. Тогда для их количественного расчета прибегают к экспериментальному определению равновесий. Оно позволяет во многих случаях не только измерить константы равновесия, но и сделать полезные, а часто и наиболее точные расчеты других термодинамических функций — энергии Гиббса, тепловых эффектов и т. д. Методы экспериментального определения констант равновесия основаны на анализе состава реакционной смеси после достижения ею состояния химического равновесия. Для получения надежных результатов кроме обычной проверки на воспроизводимость необходимо ставить эксперименты таким образом, чтобы состояние равновесия достигалось с разных сторон, т. е. при первоначальном протекании как прямой, так и обратной реакции (в разных опытах). Только совпадение (в пределах ошибки опыта) аналитических данных по составу реакционной массы может в этом случае гарантировать, что изучается истинное равновесие. Основные экспериментальные приемы для измерения констант равновесия делятся на две группы: J) статические методы; 2) динамические методы. При статических методах используют периодический реактор и ведут процесс до тех пор, пока результаты анализа реакционной массы не окажутся практически совпадающими. Начиная с этого момента, кинетические кривые для всех продуктов будут параллельны оси абсцисс, что и отвечает состоянию равновесия, исходя из которого при известной стехиометрии можно вычислить константу равновесия. Динамические методы основаны на использовании непрерывных реакторов вытеснения и особенно удобны для изучения равновесия гетерогенно-каталитических реакций. В этом случае постепенно увеличивают время пребывания реакционной смеси в аппарате, пока на выходе не будет достигнут практически постоянный состав, соответствующий равновесию. В обоих методах необходима постановка ряда опытов с варьированием начальных концентраций (парциальных давлений) веществ и расчетом средней константы равновесия при данной температуре. Нахождение констант для нескольких температур позволяет воспользоваться интегральной формой уравнения П-7)
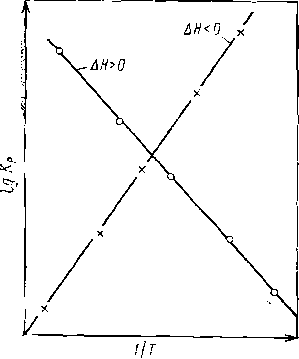
где lgKo— постоянная интегрирования. Графически в координатах lgKp—1/Т экспериментальные данные для достаточно узкого интервала температур укладываются на прямую (рис. 3); по ней и находят значения ∆Н0 и lgKo- Из этих же данных легко вычислить для каждой температуры ∆G0 = —RTlnKpи по ти изменение энтропии реакции. Когда энтальпия, энтропия и энергия Гиббса образования неизвестны только для одного из реагентов илн продуктов, данный метод позволяет весьма точно их определить. Таким способом найдены многие из табличных термодинамических функций, о которых говорилось раньше.
Для жидкофазных реакций экспериментальное определение констант равновесия более сложно. Как мы видели выше, для идеальных или близких к ним систем следует находить из опытов КN, но часто пользуются константой равновесия, выраженной через концентрации, между которыми нередко имеется существенная разница. Для неидеальных систем точное определение констант равновесия связано с дополнительным исследованием давления паров над растворами компонентов и их активности. Этим часто пренебрегают и подбирают из опытов некоторую среднюю величину Knили Кс, сохраняющуюся более или менее постоянной при варьировании начальных концентраций реагентов и продуктов. Например» при синтезе пентилтрихлор ацетат а при 100 °С в жидкой фазе
При известных константе равновесия, определенной тем или иным из рассмотренных выше методов, и начальном составе смеси (Pi,о, Ci,o) становится возможным рассчитать состав равновесной смеси (равновесные Сi, Рi выходы Xiи степени конверсии ХА), а также найти их зависимость от условий проведения процесса. Единственная обратимая реакция. Если при газофазных реакциях число молей веществ и объем реакционной смеси не меняются, проще всего в уравнении Кр=ПРiviзаменить равновесные парциальные давления веществ на их начальные давления и равновесные .степени конверсии, например PA = Ра,о (1—Ха). При избытке второго реагента используют введенное ранее мольное соотношение реагентов BY=Py,o/Pa,o. В результате находятХа, являющуюся достаточной характеристикой баланса единственной обратимой реакции.
Пример. Для газофазной реакции
Из рассмотренного примера видно, что для газофазных реакций, не сопровождающихся изменением объема, равновесная степень конверсии не зависит от РА,о. На нее влияет лишь избыток второго реагента Y, с увеличением которого растет и ХA. Это широко используют в технологии, когда применяют избыток более дешевого реагента для смещения равновесия. Объем реакционной смеси обычно является постоянным для любых жидкофазных реакций, что позволяет использовать тот же метод расчета, но с заменой давлений на концентрации или мольные доли. Пример. Для жидкофазной реакции
константа равновесия равна Кс— 4. Найти состав равновесной смеси, если реакция проводится без посторонних растворителей прн 4-кратном мольном избытке бензола У но отпошению к диэтилбензолу А. Ввиду близкой плотности всех комнонентов ее можно принять одинаковой и равной 870 г/л.
Обозпачим равновесную концентрацию диэтнлбензола через СА, а исходную через С а,о- Тогда, по условию, равновесные концентрации бензола и этилбензола составят: Если объем реакционной смеси при газофазных реакциях изменяется, расчет состава несколько усложняется. Расчет можно провести с помощью введенного ранее коэффициента изменения объема, е, выражая через него Ра,о,Byи ХA равновесные парциальные давления всех веществ. В термодинамике более принят способ парциальных молярных балансов, составляемых на 1 моль основного реагента А. Пример. Реакция гидрирования бензола в циклогексан
проводится без посторонних разбавителей при общем давлении P0бщ и мольном соотношении водорода и бензола в исходной смеси, равном BУ. Вывести общие уравнения для равновесных парциальных давлений всех веществ и для степени конверсии бензола ХАесли константа равновесия равна Кр- Рассчитать равновесную степень конверсии бензола при. BY=3 и BY=10, Р0бщ= = 0,1 МПа и РОбщ=1,0 МПа, если КР= 13800 МПа-3. Это уравнение четвертой степени решается способами вычислительной математики. Из всех его корней только одни удовлетворяет условию 0<Х,А<1... Для заданных Рoбщ и Byполучаем следующие значения: XA
Из примера видно, что для реакций, сопровождающихся уменьшением объема реакционной смеси, на смещение равновесия вправо положительно влияет не только избыток второго реагента, но и увеличение общего давления, что широко используется в практике. Наоборот, для процессов, идущих с увеличением объема, благоприятно снижение давления реагентов, в том числе за счет их разбавления инертными веществами. Пример, Для реакции дегидрирования этилбеизола в стирол
вывести общее уравнение зависимости XA от общего давления Робщ и коэффициента разбавления этилбензола водяным паром Bo=PH20/PA,о. Рассчитать ХA при Poбщ=0,1 МПа, Ро=0 и j3o=10, а также при /3Общ = 0,1 и 0,01 МПа в отсутствие разбавителя, если Кр=0,015 МПа. _ Составляем парциальный молярный баланс и находим Pi:
Системы из двух и более обратимых реакции. Для них искомыми величинами при расчете являются равновесные парциальные давления, концентрации (мольные доли)’ или выходы всех ключевых веществ, число которых определяется числом независимых реакций. Для каждой из этих реакций составляют уравнение равновесия и находят решение из системы алгебраических уравнений методами вычислительной математики при.помощи ЭВМ.
Например, при дегидратации этанола протекают две независимые обратимые реакции: из которых при известных Kр,1, Kр,2 и Робщ находят равновесные выходы *в и лгс. Так, при 423 К Кр,i= 1,62 МПа_и Кр,2 = = 51,5,_откуда при РОбщ = 0,1 МПа получим xb = 0,888, xс = 0,084 и ХА=xb+xc= 0,972. Аналогичным образом рассчитывают равновесный состав реакционной смеси для последовательных и более сложных систем обратимых реакций.
Рассчитать для РОбщ=0,02 МПа и температуры 800 К, когда Kp,i = = 0,0172 МПа и Кр,2—0,00112 МПа, равновесные выходы н-бутеиа н бутадиена, а также равновесную стенень конверсии н-бутапа, если реакция протекает без посторонних разбавителей. На 1 моль исходного н-бутана в равновесной смеси содержится (в моль): н-бутана
1-xв-хс, н-бутена хв, бутадиена хсн водорода xb+2xc, откуда сумма молей равна 1-xb-xc-+xb+xc+xb+2xc=1xb+2xc Парциальные давления веществ при равновесии составят Реакцию проводят при Р0бщ = 5 МПа иТ=623 К. Требуется найти равновесные выходы продуктов и степень конверсии аммиака, если мольное соотношение метанола и аммиака в исходной смесн составляет ру. Из трех обратимых реакций диспропорционнрования независимы только две, из которых выбираем первую и третью. Рассчитываем для них по термодинамическим данным необходимые величины:
Рис. 4. Зависимость равновесных концентраций продуктов аммонолиза метанола от мольного соотношения (B) спирта и аммиака.
Двух уравнений для нахождения трех неизвестных недостаточно. Дополнительное условие дается балансом но метанолу
который верен прн By<3, так как при ввиду необратимости реакций алкилирования единственным продуктом будет триметиламин. Решения трех уравнений нри разном даны в графическом виде на рнс. 4, из которого видно, что равновесные выходы промежуточных продуктов имеют максимумы. В заключение отметим, что термодинамика позволяет рассчитывать равновесия любых реакций, в том числе суммарных. Однако наиболее правильно проводить эти расчеты для каждого из протекающих в системе обратимых превращений. В противном случае иногда можно даже прийти к неверным выводам об осуществимости процесса. Так, для суммарной реакции
значение G°>>0 при всех доступных температурах. Это показывает, как будто, что ее невозможно провести. В действительности же эта суммарная реакция состоит из двух последовательных: 1. Какая разница между изменениями энергии Гиббса Gи стандартной энергией Гиббса G0? Какая из них при равновесии равна нулю? 2. Можно лн, изменяя температуру, сделать самопроизвольный процесс самопроизвольным и наоборот? Каким образом это осуществить для разных реакций? ' 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

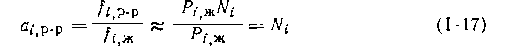 поскольку в стандартных состояниях можно считать fi, Ж = Pi:, ж- Это означает, что для таких, наиболее простых, случаев равно-
поскольку в стандартных состояниях можно считать fi, Ж = Pi:, ж- Это означает, что для таких, наиболее простых, случаев равно-


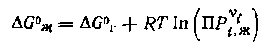


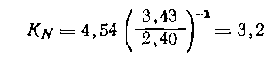


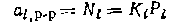








 Незначительное изменение КN при изменении исходного мольного соотношения реагентов более чем в три раза позволяет принять ее постоянной и использовать среднее значение KN=5,84 для расчета равновесных степеней конверсии.
Незначительное изменение КN при изменении исходного мольного соотношения реагентов более чем в три раза позволяет принять ее постоянной и использовать среднее значение KN=5,84 для расчета равновесных степеней конверсии.


 найти состав равновесной смеси и равновесную степень конверсии, если Кр = 15иреакция проводнтся при 2-кратиом мольном избытке спирта по отношению к кислоте и общем давлении «0,120 МПа.
Согласно материальному балансу, имеем при равновесии:
найти состав равновесной смеси и равновесную степень конверсии, если Кр = 15иреакция проводнтся при 2-кратиом мольном избытке спирта по отношению к кислоте и общем давлении «0,120 МПа.
Согласно материальному балансу, имеем при равновесии:
 откуда получаем квадратное уравнение:
откуда получаем квадратное уравнение:
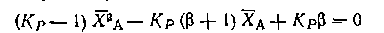

 Из выражения для константы равновесия имеем:
Из выражения для константы равновесия имеем:





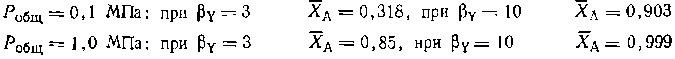









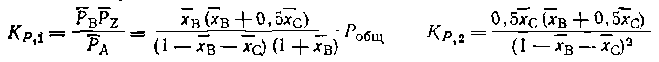
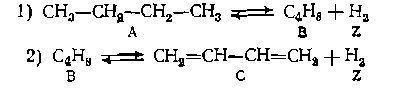
 откуда имеем расчетные уравпения:
откуда имеем расчетные уравпения:
 При РОбщ=0,02 МПа получаем: .гВ = 0,608, хс=0,075 и Ха = *в+яс =0,683. Пример 2. При аммоиолизе метанола
При РОбщ=0,02 МПа получаем: .гВ = 0,608, хс=0,075 и Ха = *в+яс =0,683. Пример 2. При аммоиолизе метанола