
|
|
РАСЧЕТ КОНСТАНТ РАВНОВЕСИЯ ГАЗОФАЗНЫХ РЕАКЦИЙ ПО ТЕРМОДИНАМИЧЕСКИМ ДАННЫМДля газов и паров за стандартное принято состояние вещества в виде идеального газа при давлении 1 ат (0,1013 МПа≈0,1 МПа). Именно для такого состояния и температуры 298 К в термодинамических таблицах, имеющихся в монографиях и справочниках, приводятся данные о стандартной энергии Гиббса и энтальпии образования соединений из простых веществ, а также об их абсолютной энтропии. Первые две величины обозначают ∆G°/f,298 и ∆H°f298(где индекс / происходит от англ. formation), а последнюю S°298- Если соединение при.указанных условиях (1 ат, или 0,1013 МПа, и 298 К) является, жидким или твердым, эти данные соответствуют его фиктивному состоянию в виде идеального газа. В свою очередь, ∆G0/,298 и ∆H°f,29 8 относятся к образованию соединения из простых веществ (02, Н2, С и др.) в их обычном для 0,1 МПа и 298 К газообразном, жидком или твердом состоянии в виде наиболее стабильной модификации (значения ∆H°д298 и S°290для некоторых органических веществ приведены в. качестве примера ниже, в табл. 3). Изменение соответствующих характеристик при химической реакции нетрудно вычислить как их сумму для продуктов и исходных реагентов с учетом величины и знака стехиометрических коэффициентов:
Если .в реакции участвуют простые вещества, то для них ∆H0и ∆G0при всех температурах приняты равными нулю, но надо учитывать их абсолютную энтропию. После расчета ∆G°298, если необходимо, определяют величину AG°tпри интересующей температуре реакции, для чего существует ряд способов. Перед рассмотрением их отметим, что входящая в уравнение (1-1) активность для идеального газа равна соотношению его парциальных давлений в данном и стандартном состояниях Pi/Pi°.В технической системе единиц Pi°равнялось 1 ат, поэтому безразмерная активность идеального- газа равнялась его давлению в атмосферах. Этому соответствовала и величина Kp=ПPiVi, имеющая размерность aTViи находимая по уравнению AG°T = —RTlnKp. Наиболее простой способ расчета констант равновесия для идеальных газов, пригодный для приближенной их оценки или В действительности при точном расчете Кр = 0,190 МПа.
При подобном расчете иногда выражают константу равновесия как функцию температуры в соответствии с уравнением:
По нему легко предсказать область температур, при которой константа равновесия становится достаточно большой. В действительности термодинамические функции определенным образом зависят от температуры, что нужно учитывать при точном расчете равновесий. Для энергии Гиббса эта зависимость такова:
Практическое применение этого уравнения осложняется тем, что стандартное изменение энтальпии реакции также зависит от температуры в соответствии с законом Кирхгоффа:
В уравнении (1-8) Cp представляет собой разность изобарных теплоемкостей' продуктов и исходных веществ, которую рассчитывают с учетом стехиометрии процесса:
Одно из приближенных его решений, предложенное Темкиным и Шварцманом, основано на применении регрессионного уравнения зависимости теплоемкости веществ от температуры:
a∆a, ∆b, ∆c—суммы коэффициентов уравнений теплоемкости для реагентов и продуктов, полученные в соответствии с уравнениями (1-11) и (1-9). Интегралы Темкина — Шварцмана Мo, М1, М2, М-1и М-2, включающие под знаком второго интеграла температуру в соответствующей степени, зависят только от температуры. Они заранее рассчитаны с интервалом в 50 и 100 гра-
дусов, а внутри расчетных интервалов значения каждого интеграла следует находить интерполяцией (табл. 1).
Пример. Дегидрирование этанола в ацетальдегид
В уравнении (1-13) /, как и ∆Но0, является константой интегрирования, следовательно, расчетная форма уравнения должна включать две численные величины I ,н ∆H°0, которые могут быть, найдены из соответствующих экспериментов. Так, если известны ∆G0или константы равновесия реакции при двух разных температурах, то их подстановка в левую часть уравнения (I-I3) позволяет найти I н ∆H°о. Если имеются данные о тепловом эффекте,, то можно найти ∆Н°о, и тогда достаточно знать ∆G0 при той же или при иной температуре, чтобы, зная H°о, вычислить I.Возможны и некоторые другие варианты, но очевидно, что для расчета двух постоянных интегрирования всегда требуется не менее двух экспериментально найденных величин ∆G0или их сочетания с ∆H°, ∆S° и т. д.
По своей точности такой расчет ∆G°Tне может превосходить метод Темкина — Шварцмана. Равновесие для реальных газов. При повышенном давлении или в состоянии, близком к насыщенному пару, газы перестают быть идеальными, и для них используют выражения констант
равновесия и изотермы Вант-Гоффа через активности [(1-1) и (1-3)]1. Чтобы сохранить общий вид термодинамических зависимостей для реальных газов, введено понятие летучести, или фугитивности /, удовлетворяющее условию dG=—RTdlnf.При этом стандартная летучесть f°принята равной летучести газа в идеальном состоянии при давлении 0,1013 МПа. Активностью называют соотношение летучестей реального газа в данном и стандартном состояниях (ai = fi/fi°), а коэффициентом летучести— соотношение его летучести и парциального давления (Yi = =fi/Pi).При давлении 1 ат реальный газ можно принять за идеальный, и поэтому /°= 1 ат. Тогда
где Р{ выражено в ат. Для идеального газа Yi =1, ai =PiВ случае реального газа коэффициент летучести находят по принципу соответственных состояний, согласно которому значения у для реальных газов являются одинаковыми, если газы находятся при тех же приведенных Температурах 0 = Т/Ткр и давлениях л = Робщ/Ркр (при определении л берут не парциальное давление, а общее, так как газ испытывает влияние всех компонентов смеси, а для водорода вместо критических параметров используют Ркр+8 ат и Tкр+8 К). Все это позволяет использовать для нахождения у любых реальных газов одни и те же графики или таблицы (табл. 2). Изотерму Вант-Гоффа для реальных газов можно преобразовать в следующую форму:
Здесь Кр выражено в ат, а Ку = ПYivi является произведением коэффициентов летучести участников реакции в степени, равной их стехиометрическим коэффициентам с соответствующим знаком. Следовательно, для расчета искомой величины Кр для реалъных газовых смесей необходимо: 1) найти, как- для- идеальных газов, ∆G0tн по ней величину InKa=— ∆G°t/RT;2) по приведенным параметрам определить YiиКпосле чего вы 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|








 В соответствии с уравнением (1-8) и дифференциальным выражением TdS = CpdTполучаем такие интегральные зависимости
В соответствии с уравнением (1-8) и дифференциальным выражением TdS = CpdTполучаем такие интегральные зависимости




 или 0,00236МПа .(по экспериментальным данным 0,0121 ат, или 0,00122 МПа).
или 0,00236МПа .(по экспериментальным данным 0,0121 ат, или 0,00122 МПа).
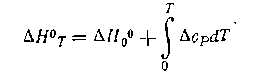



 или
или


 Для 200 °С оно дает lgКр = 1,596, Кр=0,02536 ат (0,002569 МПа), что близко к результату предыдущего расчета.
Для 200 °С оно дает lgКр = 1,596, Кр=0,02536 ат (0,002569 МПа), что близко к результату предыдущего расчета.


