
|
|
БЕЗРАЗМЕРНЫЕ ХАРАКТЕРИСТИКИ МАТЕРИАЛЬНОГО БАЛАНСА РЕАКЦИИ.ПРЕДИСЛОВИЕ Курс теории химических процессов основного органического и нефтехимического синтеза является первой специальной дисциплиной, призванной заложить научные основы для последующего изучения химии и технологии данной отрасли промышленности. Он опирается на предшествующий курсы, особенно на органическую к физическую химию, вычислительную математику и вычислительную технику, процессы и аппараты химической технологии, раздел химических реакторов в общей химической технологии; излагаемый в них материал в данном курсе расширяется и углубляется применительно к. химическим процессам основного органического и нефтехимического синтеза. Авторы старались свести к минимуму возможные повторения с перечисленными выше дисциплинами и именно по этой причине из данного издания исключены главы, посвященные механизмам нуклеофильных и электрофильных реакций (они достаточно изучаются в органической химии и, кроме того, часть материала перенесена в главу гомогенного катализа), а также методику планирования эксперимента (который хорошо представлен в курсе вычислительной математики и вычислительной техники), С другой стороны, существенно модернизированы и расширены главы, посвященные основам кинетического исследования, гетерогенному и особенно гомогенному катализу. В связи с растущим значением методов математического моделирования н оптимизации большое внимание в книге уделяется научно обоснованному количественному исследованию и расчету химических процессов, закономерностям разных типов реакций и видов катализа с точки зрения их интенсивности и селективности, построению кинетических моделей, основанных на механизме химического процесса и его физической модели, применению полученных данных для предсказания наиболее благоприятных (или оптимальных) условий практической реализации процесса. В книге имеется значительное число примеров и задач исследовательского или расчетного характера. К каждой главе даны вопросы и упражнения, которые могут служить длясамо' проверки в усвоении материала и для более углубленного его изучения. С этой же целью в Московскомхимикотехнологи ском институте им. Д. И. Менделеева, где этот курс читается уже около 20 лет, по разным его разделам выдают студентам домашние задания по расчетам химических процессов или обработке опытов. Имеется также лабораторный практикум, в котором проводится исследование химических процессов путем их моделирования на ЭВМ или же исследование на экспериментальных установках с обработкой результатов опытов на ЭВМ. Данное издание учебника значительно переработано по сравнению с первым, вышедшим в 1975 г., Н. Н. Лебедевым заново написаны введение, главы II и VII, а В. Ф. Швецом — глава III. Им же переработана глава IV, Н. Н. Лебедевым и М. Н. Манаковым — главы I и VI, Н. Н. Лебедевым — глава V. Авторы выражают благодарность В. Н. Сапунову и М. Г. Макарову за ценные консультации, М. Г. Макарову и Т. В. Бухаркиной за подготовку ряда примеров и их расчет на ЭВМ, а также коллективу кафедры химии и технологии основного органического синтеза Московского института тонкой химической технологии им. М. В. Ломоносова за внимательное рассмотрение рукописи и сделанные замечания. Авторы надеются, что книга будет полезна инженерам и научным работникам данной или смежных отраслей промышленности и заранее выражают признательность за отзывы и критические замечания, которые могут быть ценными при дальнейшей переработке учебника. Первичной основой учения о химических превращениях веществ является стехиометрия, на которой базируются все количественные соотношения при химических реакциях. В технике количества веществ чаще всего выражают через их массу mi,измеряемую в г, кг или т. Однако при химических реакциях вещества расходуются и образуются в мольных соотношениях, и поэтому для материальных расчетов более удобны их мольные количества ni, выраженные в моль или кмоль. Они связаны с массой соотношением
где Mi— молекулярная масса вещества, что позволяет после расчета в молях легко перейти к единицам массы. Мольные количества веществ ni вполне подходят для характеристики периодических процессов. В непрерывных условиях, когда вещества подают и выводят из реактора непрерывно, более приемлемой материальной характеристикой является мольный поток, который для стационарного режима процесса выражается уравнением
СТЕХИОМЕТРИЯ РЕАКЦИИ И МАТЕРИАЛЬНЫЕ РАСЧЕТЫ С точки зрения стехиометрии все химические реакции подразделяют на простые и сложные.
Простые реакции характеризуются тем, что при них протекает единственное необратимое превращение и не образуется иных стабильных продуктов, кроме записанных в уравнении реакции:
Рис. 1. Изменение мольного соотношения веществ при простых реакциях.
а также более сложные системы, включающие сочетания этих трех типов сложных реакций. Среди веществ, участвующих в сложных реакциях, различают исходные реагенты и продукты. Среди исходных реагентов один — обычно основной (более дорогостоящий или определяющий основную схему превращений). В дальнейшем его обозначаем через А. Из продуктов реакции один является целевым, ради которого реализуется весь процесс. Целевой продукт обозначим буквой В. Остальные продукты реакции называют побочными. Соответственно этому реакция образования целевого продукта называется целевой, а остальные — побочными. При анализе известной системы сложных реакций прежде всего необходимо определить число стехиометрически независимых превращений, уравнения которых нельзя получить комбинацией уравнений других реакций (сложением, вычитанием, умножением стехиометрических коэффициентов на постоянные множители). В большинстве случаев это легко сделать последовательным исключением стехиометрически зависимых реакций. Так, при обратимом превращении уравнение обратной реакции легко получить, умножив на минус единицу уравнение прямой реакции; следовательно, в этом случае имеется только одно независимое превращение. В системе сложных реакций дегидратации этанола
исключив реакцию —2 (как обратную второй) и реакцию 3 (уравнение которой можно получить вычитанием уравнения 2 из уравнения 1), находим, что система имеет лишь две независимые реакции. В. более сложных случаях для определения числа (R) стехиометрически независимых превращений используют методы матричной алгебры, составляя стехиометрическую матрицу, строки и столбцы которой соответствуют определенным вещест вам и реакциям. Для предыдущей системы стехиометрическая матрица будет такой:
Оказывается, что ранг стехиометрической матрицы равен числу независимых реакций. Определяя ранг приведенной матрицы, находим R = 2. Одновременно с числом независимых реакций определяют равное ему число так называемых ключевых веществ, по которым можно полностью охарактеризовать материальный баланс системы. В простой реакции ключевое вещество только одно (например, циклогексен из предыдущего примера). В сложных системах выбор независимых реакций и ключевых веществ взаимосвязан и определяется тем, чтобы в каждой независимой реакции участвовало хотя бы одно ключевое вещество и в то же время выбранные ключевые вещества участвовали бы только в одной или в некотором минимуме независимых реакций. Так, для дегидратации этанола выгодно выбрать в качестве независимых реакций 1 и 2, а в качестве ключевых веществ — этилен и диэтиловый эфир. Выбор ключевых веществ зависит также от простоты и точности их аналитического определения. После анализа сложной системы превращений, выбора независимых реакций и ключевых веществ легко провести ее материальный расчет. Для каждой из независимых реакций по аналогии с выражением (0-3) можно записать уравнения полноты реакции
где индекс iсоответствует веществу, а индекс j — реакции. Тогда, имея в виду, что каждое из веществ может участвовать в
Зная начальные условия и ni; (или Fi) для ключевых веществ, находим вначале по уравнениям (0-5) полноту реакций njили Fjи затем полный состав реакционной массы. Отметим, что при обратимых реакциях с единственным независимым превращением и одним ключевым веществом справедливы уравнения баланса, выведенные ранее для простых реакций, в том числе соотношения, иллюстрированные на рис. 1.
Тогда
На основе этого расчета составляется таблица материального баланса, в которой сопоставляются взятые и полученные количества веществ. Например, для предыдущего расчета получим:
При балансовых опытах или подведении фактического материального баланса установки обычно наблюдается небольшое расхождение между суммами взятых и полученных веществ. Это объясняется неточностью анализов и неучтенными потерями. Материальные расчеты удобно проводить по независимым суммарным реакциям образования ключевых веществ из исходных реагентов. В рассмотренном выше примере они совпадают с соответствующими простыми реакциями, но в другихслучаях бывает не так. Например, при этилировании бензола протекают следующие простые реакции:
Стехиометрический анализ показывает, что из четырех простых реакций две являются независимыми. Столько же имеется и ключевых веществ, за которые можно принять два вещества, выделенные жирным шрифтом,— этилбензол и диэтилбензол. Суммарные реакции их образования из исходных реагентов таковы:
реакций. Поэтому дальнейший расчет при заданных начальных условиях и Fi(ni) для ключевых веществ проводится аналогично. Уравнение (0-5) для суммарных реакций образования ключевых веществ служит для составления баланса по исходным реагентам, который часто необходим при исследовании или расчете процесса. Когда каждое из ключевых веществ образуется только по одной суммарной реакции, имеем:
БЕЗРАЗМЕРНЫЕ ХАРАКТЕРИСТИКИ МАТЕРИАЛЬНОГО БАЛАНСА РЕАКЦИИ. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

 где t - время, за которое подают или выводят из реактора niмолей вещества.
где t - время, за которое подают или выводят из реактора niмолей вещества.

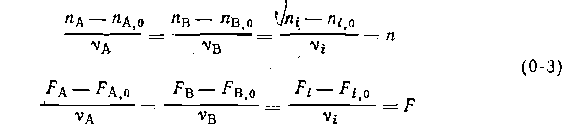












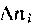












 •Одна из них совпадает с соответствующей простой реакцией, а другая не совпадает и имеет иные стехиометрические коэффициент
•Одна из них совпадает с соответствующей простой реакцией, а другая не совпадает и имеет иные стехиометрические коэффициент
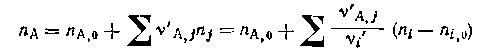 Например, для предыдущего процесса этилирования бензола получим:
Например, для предыдущего процесса этилирования бензола получим:
