КООПЕРИРОВАНИЯ И «СПРАВЕДЛИВОГО ДЕЛЕЖА»

Математические модели строгого конфликта с опорой на собственные силы — это достаточно грубый инструмент анали­за, чтобы им можно было напрямую пользоваться на практике. Учитывая объективную прагматическую слабость антагонисти­ческих игр, для оценки рисков на основе принципов не только индивидуальной, но и альтернативной полезности, коопериро­вания и «справедливого» дележа, большое распространение по­лучили специфические формы моделирования при исследова­нии конфликтных ситуаций — деловые игры (ДИ).

Однако мало кому известно, что родились ДИ в нашей стра­не. Еще в 1930 г. в Ленинградском инженерно-экономическом институте была организована так называемая группа пуска ново­строек. В результате ее исследований было установлено, что од­ной из важнейших причин неудач и задержек в запусках круп­ных заводов являлась нехватка опыта у руководящих кадров. Первая деловая игра была проведена в июне 1932 г.

Глава 4. Управление рисками в условиях конкуренции

За несколько следующих лет было разработано около 40 ши­рокомасштабных ДИ (для тренировки диспетчеров; по отработ­ке аварийных ситуаций в энергетике и других отраслях промыш­ленности; по перестройке производства и т.п.). К сожалению, в конце 1930-х годов ДИ в нашей стране были преданы запрету и забвению вслед за такими науками, как кибернетика и генетика. В середине 50-х годов за развитие ДИ взялась Американская ас­социация менеджмента. В итоге к 1980 г. в США насчитывалось около 1000 деловых игр. Вообще-то, ДИ — это моделирование по определенным правилам реальных ситуаций с целью отработ­ки навыков приятия решений. Основной элемент игры — моде­лирование ситуации, близкой к реальной. Имитация отдельных этапов реального процесса позволяет провести эксперимент не в реальных условиях, а на вербальных (описательных) и математи­ческой модели этого процесса. Это особенно важно при изуче­нии сложных экономических и общественных процессов.

Первоначально деловая игра предполагала участие в ней опытного эксперта, способного задать исходные условия для имитационной модели и затем оценить результаты действий уча­стников, но людей, обладающих экспертными знаниями, понят­но, немного и этот факт существенно тормозил распространение деловых игр на начальном этапе массового обучения. Важно иметь в виду, что с самого своего зарождения ДИ предполагали коллективную форму, то есть взаимодействие нескольких игро­ков, принимающих решения. Появление ЭВМ и дисплейных классов легко переносили коллективный вариант игры в вычис­лительную среду, моделирующую внешние условия, и роль экс­перта (анализ и оценка действий участников) частично перехо­дила к ЭВМ (подводит итоги и комментирует окончательные ре­зультаты по-прежнему руководитель игры).

С появлением вычислительной техники ситуация постепен­но изменялась, изменилось и распределение ролей между чело­веком и машиной. Роль эксперта доверили компьютеру. Первая компьютерная ДИ была создана в США в 1956 г. и моделировала деятельность фирм-производителей и их конкуренции на р ы н к е готовой продукции.

Теперь за 2-3 часа можно пройти гораздо больше циклов иг­ры, чем прежде, например «прожить» несколько лет в роли ди­ректора предприятия. Теперь компьютерные ДИ позволяют об­ходиться без партнеров и даже без преподавателя, выполняя

Риск -менеджмент

роль неких тренажеров, которые можно использовать для само­совершенствования. В итоге ДИ оказались весьма эффективны­ми по результатам обучения персонала. Исследования еще 60-х годов показали, что при сравнении ДИ с соответствующей ей по содержанию лабораторной работой в традиционной форме уров­ни усвоения знаний существенно различаются. Так, в игровой группе он составил 79,3%, а в группе, непосредственно выпол­нявшей лабораторную работу, — 54%; через две недели — 64,9 и 11,8% соответственно, через 4 недели — 49 и 8,5%, через 6 недель и далее — 32 и 5%.

Все указанные особенности ДИ предпринимателю следует обязательно знать, а при необходимости — применить этот ап­парат на практике, особенно если нет возможности (знаний, умений, навыков, денег, времени и пр.) для математического моделирования. Предприниматель в сравнительно короткие сроки и при минимальных затратах может получить важные практические рекомендации для решения возникшего двух- или многостороннего конфликта. Для этого порой бывает достаточ­но всего лишь 3—4 человек и отдельного помещения. Главным методическим приемом в такой мини-ДИ является назначение одного из лучших своих сотрудников так называемым «адвока­том дьявола». Разыграйте с этими людьми простую сценку: вы предпринимаете какие-то действия, которые, как вам кажутся, не раз опробованы вами лично, или об их эффективности вам известно от доверенных лиц, или — они являются вашим экс­промтом.

Поручите человеку, назначенному «адвокатом дьявола», быть вашим оппонентом. Пусть это для него вы делаете деловые предложения и должны убедить вашего «противника» в правиль­ности предлагаемого вами пути разрешения возникшего кон­фликта. И пусть этот человек внимательно анализирует ваши предложения и действия. Пусть он импровизирует с одной-единственной целью — находить слабые места, жестоко крити­ковать и разрушать все, что бы вы ни предложили. Но не голо­словно, а аргументированно. Тогда вы получите хорошую мо­дель будущего. Здесь вы увидите много нового для анализа как самого конфликта, так и вашей позиции на переговорах. Будьте изобретательны, постоянно ищите, как повернуть ситуацию в конструктивное русло, как вывернуться из-под огня критики оппонента. И пусть в ходе этой мыслительной дуэли еще один

Глава 4. Управление рисками вусловиях конкуренции

человек (а лучше — два) фиксирует все происходящее на видео­камеру. В крайнем случае - на магнитофон, в самом худшем -«на карандаш». Проведите «блиц-турнир» с назначенным вами «адвокатом». Отдохните. Соберите всех, кто будет участвовать в будущей акции по разрешению конфликта. Продемонстрируйте им все полученные документальные материалы по ДИ. Можете не сомневаться — не только они, но и вы сами увидите для себя много нового. Обсудите увиденное. Подумайте вместе над буду­щим. Будет, наверняка, полезно.

И все же, если есть хоть какая-то возможность, изучите мате­матические методы анализа. Для этого не надо каких-то сверх­мощных способностей. Аппарат игр с нестрогим соперничест­вом покажется вам достаточно простым, если вы уже уверенно оперируете понятием гарантированного результата и усвоили аппарат матричных игр. Нужно только дополнить эти знания пониманием основных формальных допущений в математиче­ских моделях нестрогого конфликта. Эти допущения сводятся к следующему:

>•каждый игрок имеет свою функцию выигрышей, v,(a,, Z>_;)и v₂(a,., bj), причем для большинства ситуаций игры ока­зывается, что v,(a₍, b,) ф (-v₂(a₍, b );другими словами, один из игроков не всегда выигрывает ровно столько, сколько ему проигрывает другой; > • имеется хотя бы одна ситуация (кроме ситуации равнове­сия в максиминных стратегиях игроков), для которой ин­тересы игроков совпадают или весьма близки; >-каждый из игроков намерен использовать все свои страте­гические возможности, к которым он не прибегал в анта­гонистической игре. Теперь рассмотрим математические модели нестрогого кон­фликта, базирующиеся на принципах индивидуальной и альтер­нативной полезности. Наиболее простой из возможных игр, удовлетворяющих перечисленным допущениям, является так называемая биматричная игра. Эта игра формируется из двух от­дельных матриц — отсюда и название «биматричная», которыми руководствуются каждый из игроков. Принято результаты зано­сить в одну матрицу, но в каждой ячейке записывать значения двух самостоятельных функций выигрыша: первая цифра — вы­игрыш первого игрока, вторая — второго. Генеральная задача

Риск-менеджмент

каждого из игроков — максимизировать собственную функцию выигрыша.

Например, на рынке два торговца представляют каждый свой товар. Товары могут различаться по номенклатуре, по каче­ству, по цене. Каждый торговец заинтересован в максимизации собственной прибыли. При этом представленные торговцами товары могут быть коррелированы по величинам прибьши тор­говцев из-за активной роли таких факторов конъюнктуры рын­ка, как количества товаров, их потребительские свойства, време­на появления на рынке и пр. Коррелированность здесь может проявляться также и в том, что один товар может дополнять дру­гой, усиливая его потребительские качества, или выступать угне­тающим фактором для другого товара, мешая его продаже. Все эти обстоятельства приводят к тому, что разные ситуации бимат-ричной игры по-разному предпочтительны для каждого из игро­ков.

Задача анализа биматричных игр сводится к тому, чтобы за каждого из игроков оценить величины гарантированных резуль­татов, установить наличие или отсутствие ситуации равновесия, представить доводы в пользу той или иной из имеющихся стра­тегий поведения игроков. Здесь, как и в случае матричных игр, вначале проводят анализ, исходя из предположения об одно­кратной партии игры, и выявляют ситуации равновесия в чис­тых стратегиях (если таковые есть). После этого, если есть к это­му предпосылки, игру анализируют как многократно повторяю­щуюся и оценивают результаты в смешанных стратегиях.

Итак, пусть заданы множества А, В стратегий первого и вто­рого игроков соответственно и их собственные функции v, {a_n bj )v₂(a,, b_j) выигрыша, заданные на множестве {(а_п Ь,)} си­туаций игры. В общем случае полагают, что функции v,(«,., bj) v₂(fl„ неотрицательны. Обозначим через я.* и Ь' максимин-ную и минимаксную чистые стратегии, а через а" и Ь" — равно­весные чистые стратегии. Тогда для биматричной игры формулируют условие равновесия (по Дж. Нэшу) в чистых стра-

тегиях:

Глава 4. Управление рисками в условиях конкуренции

На неформальном языке эти соотношения означают, что ес­ли оба игрока придерживаются равновесной ситуации (а",Ь"), то они не могут получить меньше, чем получил бы каждый из них, если бы отклонялся от ситуации равновесия, в то время как ее придерживается другой.

Принципиальное отличие условия равновесия по Нэшу для биматричной игры по сравнению с ситуацией равновесия в мат­ричной игре состоит в следующем. Во-первых, равновесный вы­игрыш в биматричной игре для каждого из игроков не меньше по величине, чем выигрыш в максиминной ситуации равнове­сия, то есть в общем случае выполняются неравенства:

Во-вторых, в биматричной игре отклонение какого-либо иг­рока от ситуации равновесия может по-разному повлиять на вы­игрыш как самого этого, так и другого игрока. В антагонистиче­ских играх, как мы знаем, уклонение любого из игроков от ситуации равновесия, в то время как другой продолжает придер­живаться своей максиминной (или минимаксной) стратегии, приводит к ухудшению положения «уклониста» и одновремен­но — к улучшению ситуации для рационально поступающего иг­рока. А в неантагонистической игре такое же отклонение может по-разному повлиять на выигрыш другого игрока. Например, может даже оказаться, что, если оба игрока отклонятся от равно­весной ситуации, то выигрыш каждого из них может увеличить­ся. Но может — остаться прежним или уменьшиться.

Из этих двух отмеченных особенностей вытекает важный вы­вод для практического использования аппарата биматричных игр: если при анализе биматричной игры будет установлено, что равновесные выигрыши игроков существенно превосходят мак-симинные, то в таком случае им стоит подумать о перспективах применения равновесных стратегий биматричной игры. Однако необходимо помнить, что решение следовать равновесной по Нэшу стратегии сродни желанию «жить по закону»: принудить к этому нельзя, и, кроме того, в условиях, когда «все живут по за­кону», у кого-то обязательно возникает искушение нарушить за­кон, поскольку ему лично это значительно выгоднее (хотя все

Риск -менеджмент

остальные от этого могут сильно страдать). Продемонстрируем все отмеченные особенности и выводы классическими иллюст­ративными примерами [63].

«Семейный спор». Игра была разработана с целью продемон­стрировать факт присутствия в поведении индивидов достаточно противоречивых устремлений. С одной стороны, каждый стре­мится к повышению собственной выгоды (принцип индивиду­альной рациональности), с другой - каждый из этих индивидов может испытывать значительное удовлетворение от того, что он может сделать приятное другому (принцип групповой рацио­нальности). Фабула модели: муж любит хоккей, а жена - балет. Близится выходной день. Каждый из супругов стремится про­вести его как можно приятнее для себя. Но, если муж согласится пойти на балет, то жена получит максимум удовольствия, а муж будет удовлетворен только тем, что будет вместе с женой. Если же на хоккей согласится жена, то именно она будет удовлетворе на только тем, что не провела выходной одна. Если же каждый из них будет настаивать на собственном способе проведения от­дыха, будет отдыхать «своим путем»: жена — на балет, а муж — на хоккей — оба не получат удовольствия. Матрица игры имеет следующий вид:

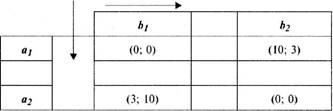
Данная модель хорошо описывает также проблемы столкно­вения интересов при совместном решении вопросов об установ­лении квот на рынке сбыта.

Предположим два конкурента (далее условно именуемые «сторона А» и «сторона 5») прибыли на переговоры об установ­лении квот на рынке сбыта определенного товара, например нефти и нефтепродуктов. Каждая из сторон прибывает со свои­ми пакетами предложений. Для простоты предположим, что у каждой из сторон две альтернативы: настаивать на принятии своих предложений (альтернативы а,и Ь,) или принять предло­жения конкурента (альтернативы a₂nb₂).

Оценим выгодность всех возможных ситуаций в порядковой шкале, считая, что если стороны не придут к соглашению, то со­храняется status quo и полезность переговоров равна нулю. Дру-

Глава 4. Управление рисками в условиях конкуренции

гие градации шкалы следующие: если принимается предложение стороны А в ущерб стороне В, то выигрыш стороны А более чем в три раза превышает выигрыш стороны В; аналогично оценива­ются выигрыши, если принимается предложение стороны В в ущерб стороне А. Для полноты анализа будем считать, что ситуа­ция, когда обе стороны соглашаются на план конкурента, также имеет нулевую ценность для обеих сторон (как невероятный случай).

В результате биматрица игры примет следующий вид:

Вначале найдем максиминные стратегии для каждого из иг­роков. Обе стратегии первого игрока являются максиминными, так как они обеспечивают ему одинаковый наибольший гаран­тированный результат (равный нулю). Оказывается, что обе стратегии второго игрока также являются максиминными и так­же дают этому игроку гарантированный результат, равный нулю.

Найдем теперь равновесные по Нэшу ситуации, пользуясь определением. Проще всего это сделать путем фиксирования, так сказать, претендентов на звание равновесных стратегий. По­кажем, как это делается при отыскании равновесных стратегий для первого игрока. Зафиксируем первую стратегию Ъ\ второго игрока, считая, что именно она претендует на роль «равновес­ной». При таком предположении наибольший результат для пер­вого игрока дает использование его стратегии а₂, поскольку вы­полняется неравенство v_l(a₂, b_{) = 3 > v_l(a_t,b_l) = 0. Теперь про­ведем сравнение стратегий первого игрока, зафиксировав в качестве претендента на роль «равновесной» вторую стратегию Ь₂ второго игрока. Получается, что первому игроку при такой ги­потезе выгоднее применить свою первую стратегию а\,посколь­ку выполняется неравенство v^a,, b₂) = 10 > v_x{a₂jb₂) = 0.

Аналогично проведем оценку предпочтительности стратегий второго игрока, предполагая поочередно, что претендентами на роль «равновесной» являются стратегии a_t и а₂ первого игрока. В результате проверки указанных гипотез получаем: v₂ (я,, Ь₂ )= 3 >

Риск-менеджмент

>v₂(a_]b_l) = О иv₂(a₂i>,) = 10 >v₂(a₂b₂) = 0. Это означает, что если на роль «равновесной» претендует стратегия а_ьто второму игроку предпочтительнее использовать стратегию Ь₂, а если фик­сировать а₂, то выгоднее будет стратегия Ь|. Предпочтения сто­рон в парной биматричной игре удобно отражать стрелками, на­правленными от более предпочтительной ситуации к менее предпочтительной. Результат применения подобного «метода стрелок» представлен на рис. 4.1. На этом рисунке предпочтения на парах стратегий игроков, выраженные при условии фиксации у конкурента претендентов на роль «равновесных», отображены в виде стрелок, направленных от более предпочтительной стра­тегии к менее предпочтительной.

Геометрически стрелки, отображающие предпочтения, схо­дятся на ситуациях {af, />/) и (а/, Ь₂). Такое согласие в предпочте­ниях конкурирующих сторон означает, что в этой игре две рав­новесные стратегии: (я/; b_t) и (а/, Ь₂). Эти две равновесные си­туации улучшают положение каждой из сторон по сравнению с ситуациями, дающими им каждой нулевой результат. Но эти равновесные ситуации принципиально различаются по пред­почтительности для сторон: одна из сторон согласно условиям получает более чем втрое по сравнению с другой. Согласятся ли стороны с таким «равновесием»?

«Дилемма заключенного». Эту игру в своеобразной интерпре­тации разработал американский ученый из Принстонского уни­верситета А. Таккер (A.W. Tucker). Этим и объясняется несколь­ко экстравагантное название модели. На самом деле ее разработ­ка была связана с поиском решения проблемы стратегической стабильности. Стороны А и В решают договориться о масштабах сокращения вооруженных сил. У каждой из сторон две страте-

Глава 4. Управление рисками в условиях конкуренции

гии: или поддерживать вооружения на прежнем уровне, или произвести существенное сокращение вооружений. В то же вре­мя эта игра хорошо демонстрирует психологию лиц, готовых поддержать любые предложения по «всеобщему и повсеместно­му исполнению законов», но — только не ими самими.

Фабула игры следующая. Окружной прокурор приказал взять под стражу двух подозреваемых в совершении дерзкого ограбле­ния. Они помещены в разные камеры и не могут переговари­ваться. У каждого из заключенных две возможности: признаться в том, что участвовал в ограблении, или запираться до конца. Если оба будут запираться, то через трое суток их вынуждены бу­дут отпустить. Если оба признаются, то они получат минималь­ное наказание.

Рассмотрим матрицу игры со следующими оценками пред­почтительности для каждого из заключенных под стражу:

Применяя «метод стрелок», получаем, что равновесной явля­ется ситуация {а2, Ь₂) — оба заключенных признаются в совер­шении преступления, — в которой их выигрыши равны по еди­нице у каждого. Но совершенно очевидно, что ситуация {a_h bj) — не признаваться — для них выгоднее. Другими словами, эта си­туация доминирует равновесную ситуацию и лучше обоим запи­раться, чем обоим признаваться. Но тут есть одно «но»: у каждо­го из подозреваемых в ситуации (а_иb,) существует мощный сти­мул признаться «в одиночку», пока его подельник запирается. И тем самым — существенно выиграть по сравнению с неустой­чивой ситуацией (a_h b,). Так запираться или признаваться? -Вот в чем вопрос...

Рассмотренные примеры являются иллюстративными в смысле условности значений выигрышей сторон. Эти выигрыши назначались нами в соответствии с простым предпочтением од­ного исхода над другим без детализации, на сколько или во сколько раз сильнее то или иное предпочтение. Для таких игр — «игр с предпочтениями» — бессмысленно говорить о примене-

Риск-менеджмент

нии смешанных стратегий. Если же биматричная игра описыва­ется в шкале полезностей не менее совершенной, чем интер­вальная, то рассмотрение смешанных стратегий оправданно, если это допустимо их интерпретацией в рамках данного кон­фликта.

Но что делать, если выигрыши, получаемые конфликтующи­ми сторонами в равновесной, по Нэшу, ситуации, их не устраи­вают? В таком случае им ничего не остается, как начать обмени­ваться информацией, блефовать, угрожать и договариваться друг с другом о совместном разрешении конфликта. Математической моделью конфликта при таких устремлениях сторон становится кооперативная и коалиционная игра. Такая игра ведется по сле­дующим правилам:

>-разрешено заключать совместные соглашения;

> допускается совместный выбор стратегий (в общем слу­чае - смешанных);

>-допускается передавать полезность от одного игрока к другому (хотя, возможно, и не всегда линейно).

Каждый из приведенных пунктов правил ведения коопера­тивных игр в целом означает следование принципу групповой рациональности. Однако последний пункт, хотя и предполагает, что игроки могут «покупать и продавать» друг другу имеющуюся в их распоряжении полезность, чтобы улучшить собственное по­ложение в игре, не накладывает каких-либо ограничений на то, как это должно делаться. А ведь принцип индивидуальной ра­циональности будет заставлять каждого, образно говоря, «тянуть одеяло на себя», а значит — индивидуальная рациональность может войти в противоречие с групповой. Другими словами, ес­ли кооперирование допускается, то сразу возникает вопрос: «Что такое справедливый дележ»?

Нэш предложил компромиссную схему [63] распределения имеющейся в распоряжении игроков максимальной полезности, которая может быть принята за модель «справедливого дележа». Суть этой схемы в следующем. Вначале устанавливают «начало отсчета». За него принимают тот минимальный результат, кото­рого игрок может достичь и самостоятельно, поэтому он не со­гласится ни на какие меньшие дележи. Понятно, что этот мини­мальный результат определяется собственными стратегически­ми возможностями каждого игрока и равен наибольшему гарантированному результату. Затем нужно вычислить прираще-

Глава 4. Управление рисками в условиях конкуренции

ния Av,(v,, v,) и Av₂(v,, v₂) полезностей игроков от согласован­ного ими дележа v,, v₂. Эти приращения составляют величины:

Av,(v,, v₂) = v, - v* и Av₂(v,, v₂) = v₂ -v₂,

V,* и v₂ — максиминные выигрыши первого и второго игроков, соответственно.

После этого формируется целевая функция <p(v,,v₂) = =AV|(v_bv₂) • Av₂(V|,v₂), и на множестве {vi,v₂} допустимых деле­жей отыскивается максимум этой функции. В результате компро­миссное решение v, и v₂ отыскивается в ходе решения задачи:

v,,v₂:max(p(v₁,v₂).

Поиск экстремума в этой задаче отражает стремление к наи­лучшему компромиссному дележу полезности между игроками. При этом большую часть общей полезности при дележе получит тот игрок, у которого минимаксный результат (то самое «начало отсчета»), или status quo, представляет более предпочтительную величину. Это примерно соответствует некой гипотетической ситуации дележа определенной суммы денег между богатым и бедным, однако саму эту сумму они получат только при условии, что смогут договориться, как ее разделить. В такой ситуации, чтобы получить хоть что-то, более бедный, скорее всего, вынуж­ден будет пойти на некоторые уступки при дележе, а богатый, у которого финансовое положение более прочное, может позво­лить себе дольше торговаться и настаивать на большей доле для себя. Рассмотрим количественный пример согласно приведен­ному вербальному описанию [63].

Двоим людям предлагают $100, если они смогут решить, как поделить эти деньги между собой. Предполагается, что первый из них очень богат, а второй имеет капитал всего в $ 100. Предпо­лагается также, что функция полезности денег логарифмиче­ская, то есть полезность любой суммы денег пропорциональна ее логарифму. Как должны быть разделены эти деньги, чтобы люди на него согласились? Обозначим через х сумму денег, ко­торую получит первый игрок. По условиям игры — это очень бо­гатый человек. Поэтому для этого игрока не будет большой ошибкой считать, что его функция полезности на интервале воз­можных значений выигрыша приблизительно пропорциональна

Риск-менеджмент

полученной сумме, то есть logx ~ х. Кроме того, для величины х выполняется очевидное условие: х < 100, то есть первый из уча­стников дележа не может получить больше, чем предложено дво­им для дележа. Так как второй участник дележа имеет вначале только $100, то приращение Av₂(v,,v,) полезности, которое он получает от своей части дележа в ($100 — х), равна

log(l00 + (100 - х)) - /oglOO = /og-'^r--.

Максиминные выигрыши v,(a',b]) и v₂(a', b'_:)обоих игро­ков, конечно же, равны нулю, поскольку, согласно условию, они смогут получить в свое распоряжение $100, если только догово­рятся о том, как их поделить. Составим выражение для целевой функции:

<р" (vj^^Av^v,^)• Av₂(V|, v₂)⁴= x • log

л

Эта функция одной переменной х. Отыскиваем оптимальное значение х⁰""""', которое максимизирует функцию ср (vi,v₂). В та­ком случае доли для дележа между участниками сделки составят: _Vl =х"""'"'" и v, =100 - х"""""' Для отыскания максимума целевой

функции <p(v,,v₂) можно применить необходимое условие суще­ствования экстремума, согласно которому в точке х"""""' экстре­мума производная от функции 9(v_bv₂) по переменной х должна быть равна нулю.

После дифференцирования и

водной мы получаем уравнение

получаем приближенно х'""""'" = 54,4. Следовательно, богатый участник сделки может претендовать на v, = $54,4, а бедный, у которого только и есть что его $100, должен согласиться на сум­му v₂ = $100 - $54,4 = $45,6. Иначе, согласно условиям, сделка не состоится.

В некотором смысле полученное решение кажется стран­ным. Из него следует, что богатый участник сделки должен по­лучить больше, чем бедный, о котором можно утверждать, что он больше нуждается в деньгах. Однако такое утверждение пред­полагает сравнение полезностеи разных лиц. А для них логариф-

Глава 4. Управление рисками в условиях конкуренции

мическая функция полезности используется на разных участках определения аргумента: для богатого — в области насыщения, для бедного — на участке интенсивного роста. Иными словами, полученное, согласно схеме Нэша, решение учитывает, что фак­тическая полезность денег у второго участника сделки убывает быстро, а у первого — медленно. В результате получается, что второй участник дележа стремится получить хоть что-то и при сделке может уступить богатому участнику.

Против решения Нэша задачи о сделках можно выдвинуть серьезное возражение, состоящее в том, что оно не принимает в расчет угрозы. И если кто-то из игроков все же не удовлетворен компромиссным решением, получаемым в ходе решения указан­ной оптимизационной задачи, он может оценить свои стратеги­ческие возможности по применению стратегий угроз.

Что мы будем понимать под стратегией угрозы? Во-первых, это некая реальная или провозглашенная в качестве возможной для применения в конфликте стратегия поведения того или ино­го игрока. Во-вторых, эта стратегия должна быть эффективна в отношении достижения цели дележа, а именно — объявление одним из игроков о намерении использовать стратегию угрозы должно склонить другого игрока к мысли, что ему выгоднее пой­ти на уступки при дележе, чем попасть в ситуацию, когда будет применена стратегия угрозы. При демонстрации угрозы пуска­ются в ход все уловки: «дымовые завесы», намеки, «пробные ша­ры», а порой и заявления на пресс-конференциях — вся извест­ная техника дипломатии бросается на запугивание и выяснение намерений друг друга. Взаимоотношения сторон делаются мно­гомерными и, в общем случае, — многополюсными. Но в своих основных моментах они, как всегда, базируются на простой, почти физической «силе».

Таким образом, эффективность стратегии угрозы определя­ется не только результатом предполагаемого истинного воздей­ствия по каким-то физическим объектам. Такое воздействие мо­жет привести к изменению состояния объектов, связей между ними, формы или качества входящих в них элементов. Кроме того, эффективность стратегии угрозы в значительной мере оце­нивается психологическим воздействием на субъекта, которому угрожают. И это психологическое воздействие приводит к тому, что у этого субъекта изменяются мнения относительно ценности тех или иных ситуаций конфликта, изменяются суждения о про-219

Риск -менеджмент

порциях дележа полезности и т.п. В-третьих, поведение угро­жающего игрока и само провозглашение стратегии угрозы долж­ны быть таковы, чтобы у того, кому угрожают, не оставалось со­мнений в том, что угроза может быть приведена в исполнение. Таким образом, стратегия угрозы эффективна только в том слу­чае, если она правдоподобна, если она может улучшить положе­ние угрожающего по отношению к тому, кому угрожают, и если она сделана обдуманно. Последнее означает, что если угроза объявлена, то угрожающий обязательно ее применит, если по­требуется.

Найти компромиссное решение в случае применения игро­ками стратегий угроз можно путем решения оптимизационной задачи, аналогичной той, которую мы только что рассмотрели. Только при формировании целевой функции вместо величин v.* и v*₂ использовать значения vf и vf, которые представляют со­бой величины полезностей игроков в ситуации, которая сложит­ся после применения игроками своих стратегий угроз. Рассмот­рим пример. Пусть биматричная игра моделируется матрицей вида:

1,4 (-2,4) (-3,-1) (4,1) '

Достаточно просто убедиться, что для этой игры имеются две ситуации равновесия по Нэшу, выигрыши в которых превосхо­дят максиминный уровень. Эти ситуации принципиально отли­чаются по предпочтительности для каждой из сторон: ситуация (a], bj) более предпочтительна второму игроку, а ситуация {а₂, Ь₂) - первому. Наибольший гарантированный результат v, игры для первого игрока равен —2 и обеспечивается этому игро­ку применением его первой стратегии. Для второго игрока его наибольший гарантированный результату* равен -1 и достига­ется применением вторым игроком также его первой стратегии. Скорее всего, такие значения выигрышей игроков устроить не могут, поскольку в данной игре они оперируют максимальной полезностью v_max = 5 (суммы выигрышей в ситуациях (а. Л) и (а₂,Ь₂) игры).

Если игра будет вестись как некооперативная и бескоалици­онная, то, согласно принципу индивидуальной рациональности, игроки применят свои максиминные стратегии и получат реаль-

Глава 4. Управление рисками в условиях конкуренции

ные (а не гарантированные) результаты, соответствующие ситуа­ции {а\,Ь\). Это, конечно, устроило бы второго игрока (его вы­игрыш стал бы равным 4), но никак не первого. В такой ситуа­ции первый игрок хотел бы применить стратегию угроз, чтобы добиться для себя некоторых уступок от второго. Какие у него в таком случае стратегические возможности? Попытаемся качест­венно проанализировать конфликтную ситуацию. Во-первых, менее предпочтительными для игроков являются ситуации (йь Ь₂) и (а₂, Ь\), более предпочтительны для них ситуации (a_t, Ь\) и (а2,Ь₂). Очевидно, что все недоминируемые дележи, среди которых следует вести поиск компромисса, представляют собой математический отрезок, соединяющий точки со значе­ниями выигрышей для ситуаций (а_иЪ\) и (а₂, Ь₂). В то же время, как мы уже отмечали, ситуация (а\,Ь\) более предпочтительна для второго игрока, а ситуация (а₂, Ь₂) — для первого.

Предположим, что первый игрок попробует угрожать приме­нить свою вторую стратегию а₂, если второй не согласится на компромиссное решение, которое будет более выгодно для него. Но будет ли такая угроза первого игрока эффективной? Оказы­вается, что нет. Очевидно, что второй игрок может легко пари­ровать эту угрозу, ответив контругрозой применить свою первую стратегию. Вроде бы второй игрок блефует, поскольку он риску­ет при этом оказаться в ситуации (а₂, Ь\), которая принесет ему явный проигрыш, равный -1. Однако такой исход сильнее нака­зывает первого игрока, поскольку его проигрыш в таком случае составит уже —3. Следовательно, позиция первого игрока в рас­сматриваемой игре весьма сложная. А вот у второго игрока есть весьма эффективная угроза — применить свою первую страте­гию.

Против такой угрозы первый игрок ничего не может пред­принять, существенно не ухудшив свое положение в игре. По­этому первому игроку следует пойти на значительные уступки при дележе общей полезности. Определим компромиссный де­леж общей полезности игроков, приняв ситуацию (а₂, Ь\) за си­туацию угрозы со значениями полезностей для игроков V|V^rP = — 3 и v₂^yrp = —1. С учетом того, что максимальная полезность ^vmax = V\+v₂ на эффективной границе равна 5, можно положить v₂ = 5 — V| В таком случае функция (p(v_bv₂) = AV|(v_hv₂) Av₂(v,,v₂) примет вид: (p(v,,v₂) = [v, -(-3)] [(5 - v,) - (-1)] = -v,²+ 3 v, + 18.

Риск-менеджмент

Максимум в этой задаче безусловной оптимизации можно также искать, применив сначала необходимое, а затем — достаточное условие существования экстремума. После несложных преобра­зований находим, что это условие выполняется для стационар­ной точки V|= 3,5 Достаточное условие для задачи на максимум состоит в отрицательности второй производной от функции по ее аргументу в стационарной точке. Это условие также выполня­ется.

Следовательно, решением рассматриваемой задачи, задаю­щим компромиссное решение Нэша в биматричной игре с угро­зами, будут значения v,= 3,5; v₂ = 15. Но если компромиссное решение, полученное в рамках модели «линейного распределе­ния полезности», не устраивает конфликтующие стороны, им остается попробовать достичь соглашения путем переговоров в ходе деловой беседы.

Не нашли, что искали? Воспользуйтесь поиском по сайту: