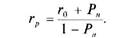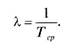АНТИКРИЗИСНОГО УПРАВЛЕНИЯ ФИРМОЙ

Оценка вероятности банкротства (Z-модель). Риск банкрот­ства достаточно распространен, причем не только в странах с переходной экономикой. Об этом свидетельствует и отечествен­ный опыт, и события последних десятилетий в зарубежных стра­нах. С 1 марта 1993 г. в России введен в действие Закон «О несо­стоятельности (банкротстве) предприятия» (от 19 ноября 1992 г. № 3929-1). Согласно этому закону под банкротством понимает­ся неспособность предприятия удовлетворять требования креди­торов по оплате товаров (работ, услуг), включая неспособность обеспечить обязательные платежи в бюджет и внебюджетные фонды, в связи с превышением обязательств над имуществом или в связи с неудовлетворительной структурой баланса. Как видно, в приведенном определении уже содержится указание на

Риск -менеджмент

главные факторы, определяющие возможность наступления это­го, далеко не безобидного экономического и юридического со­бытия. Но это не все. С формальных позиций банкротство — это событие, то есть простейшая, системная модель сложного эко­номического явления. Это явление не является статичным. Как правило, банкротству предшествует достаточно длинная полоса финансово-экономических затруднений, вслед за которыми происходит лавинообразное ухудшение финансового состояния предприятия. Динамика банкротства также нашла отражение в Федеральном законе «О несостоятельности (банкротстве)» от 26.10.02 № 127-ФЗ. В нем определены сроки наступления собы­тия банкротства. Так, юридическое лицо считается не способ­ным удовлетворить требования кредиторов, если его обязатель­ства не исполнены в течение трех месяцев с момента наступле­ния даты исполнения.

Учитывая указанные обстоятельства, банкротство можно прогнозировать, чтобы можно было своевременно принять не­обходимые меры для его предотвращения как события. Сущест­вуют разные методы прогнозирования финансового состояния предприятия с позиции его потенциального банкротства. Наи­больший интерес среди них представляют математические мето­ды, которые уже почти сорок лет широко используются в зару­бежной практике оценки риска банкротства. В частности, широ­ко известны (см., например, [66, 77, 84] и др.) так называемые Z-модели, разработанные известным западным экономистом Э. Альтманом (Altman) в конце 60-х годов XX в. (другие назва­ния этой модели: коэффициент Альтмана, индекс кредитоспо­собности). По форме модель Альтмана представляет линейную функцию от двух до семи факторов. Ее параметры рассчитывают на основе статистического обобщения финансовых показателей, характеризующих экономическую деятельность тех предпри­ятий, которые либо уже обанкротились, либо удачно избежали банкротства. Например, при построении первой своей модели Альтман обследовал около 70 предприятий США, половина ко­торых обанкротилась в период между 1946 и 1965 гг., а половина работала успешно.

Наиболее простая из моделей Альтмана — двухфакторная. В ней переменными являются коэффициент текущей ликвидности и доля заемного капитала в общей сумме источников заемных

Глава 3. Управление стохастическими рисками

средств. Модель формирует качественную шкалу для оценки ве­роятности банкротства и задается соотношением вида:

Z = -0,3877 - 1,0736 К, + 0,0579 К₂,

К₄ — отношение рыночной стоимости акций к величине заемно­го капитала;

К₅ — отношение выручки от реализации продукции к сумме ак­тивов.

По сравнению с двухфакторной моделью качественная шка­ла оценок пятифакторной модели имеет отрицательную направ­ленность по вероятности банкротства, а именно: чем больше

Риск -менеджмент

значение Z, тем меньше вероятность банкротства. Результаты расчетов позволили установить диапазон возможных откликов Z-модели. Он ограничен в пределах примерно от -15 до +20. Де­тализация этого диапазона по градациям вероятности банкрот­ства проводится различными исследователями, в целом, одина­ково. Все сходятся в мнениях, что если Z > 3, то предприятие финансово устойчиво, а если Z< 1,8 - несостоятельно. Однако в связи с тем, что в четвертом коэффициенте фигурирует рыноч­ная стоимость акций, этот показатель можно использовать лишь в отношении крупных компаний, и границы вынесения оценок здесь начинают смазываться. Тем не менее часто в литературе можно встретить почти вдвое больше качественных градаций шкалы вероятности банкротства, чем в двухфакторной модели:

>-«очень высокая», если Z < 1,8;

>«высокая», если 1,81 < Z< 2,7;

>•«возможная», если 2,8< Z< 2,9;

>-«маловероятная», если Z > 3.

Итак, основной недостаток пятифакторной модели Альтмана в том, что ее адекватность высока только для достаточно круп­ных компаний, длительное время уверенно котирующих свои акции на бирже.

Наконец, в конце 70-х годов XX в. Альтманом была разрабо­тана семифакторная модель. По некоторым оценкам, она позво­ляет прогнозировать банкротство за пять лет до его наступления с надежностью не менее 0,7. Кроме того, примерно в этот же пе­риод были разработаны модели и других авторов: Винакора и Смитира (по результатам оценки работы более 180 фирм); Фиц-патрика (исследовано 20 фирм, которые потерпели крах в 1920-1929 гг.); Мервина (изучен опыт 939 фирм в 1926-1936 гг.);Таффлера; Спрингейта; Фулмера (30 успешных компаний и 30 банкротов); Лего (были проанализированы 30 финансовых по­казателей 173 промышленных компаний Квебека) и др. Они со­держат от 4 до 9 факторов. Более подробные сведения по этим моделям можно почерпнуть в книге Ф. Робертса «Дискретные математические модели с приложениями к социальным, биоло­гическим и экономическим задачам» [77].

Дискретная аналитическая модель кредитного риска. В зави­симости от того, в каком контексте рассматривается угроза поте­ри или убытка, для оценки риска могут вполне быть использова-

Глава 3. Управление стохастическими рисками

ны модели и методы теории надежности. Пусть вначале требует­ся оценить риск для самого, так сказать, неблагоприятного исхода — полного невозвращения кредита. При таком подходе к оценке риска этот случай вполне адекватно описывается моде­лью внезапного отказа. Обозначим через Р_н — вероятность не­возвращения кредитных средств полностью в установленный срок, а через г₀ — банковскую ставку кредитования при нулевом риске. Обычно полагают, что риск незначителен, если вероят­ность Р_н < 0,25, а при уровнях вероятности Р_п >0,60 его считают критическим.

Поскольку 0 < Р_н< 1, кредитор может не получить принадле­жащие ему заемные средства С с учетом процентов, то есть он может потерять сумму (1+ г₀)С с вероятностью Р_н. Поэтому в ус­ловиях риска он стремится увеличить ставку кредитования с г₀ до г_р, ориентируясь, на средний ожидаемый доход. Этот ожидае­мый доход можно вычислить по известной формуле для матема­тического ожидания дискретной случайной величины:

Р„ ■ 0 + (1 -Р„) > (1 + г_р)С= (1 - Р_н) ■ (1 + _Гр)С.

По справедливости, это ожидаемое значение должно равнять­ся по величине той сумме, которую кредитор получил бы, если бы положил деньги в банк и не рисковал. Поэтому полагаем, что

(\-Р_н)(1₊Г_р)С:=(1+Г₀)С.

Отсюда легко определяем, что процентная ставка г_р кредито­вания в условиях риска должна быть равна

Например, для введенных нами градаций уровней 0,25 и 0,60 вероятности Р„ невозвращения кредитных средств и банковской ставке />= 0,05 кредитования значения, величины процентной ставки г_р кредитования в условиях риска составят:

r_f < 0,4 при Р_н < 0,25 и г_р > 1,625 при Р_и > 0,60.

Непрерывная модель кредитного риска. Предположим теперь, что банк постоянно выдает кредиты или учитывает векселя. Предположим, что риск невозврата кредита пренебрежимо мал.

Риск -менеджмент

Однако банк может испытывать затруднения, даже нести потери или убытки оттого, что заемщики опаздывают со сроками воз­врата или со сроком погашения векселей. При достаточно дли­тельном процессе проведения подобных кредитных и факторин­говых операций, при значительной массовости таких событий хорошей моделью для оценки риска несвоевременного возврата может служить модель простейшего (пуассоновского) случайно­го потока событий. В такой модели случайными являются мо­менты времени возврата кредитованных средств с задержкой, а следовательно, случайной является и сама величина 7 времени за­держки. Обозначим через Г_ср среднее время задержки возврата.

Среднее время Т_ср задержки возврата можно установить, на­бирая статистику по задержкам возврата за достаточно длитель­ный период наблюдений. Предположим, что среднее время Г_ср задержки возврата известно, и оказалось, что оно примерно по­стоянно за весь рассматриваемый период финансовой структу­ры. Это означает, что среднее число случайных событий — воз­вратов кредита с задержкой или опоздание с погашением вексе­лей — не зависит от того, когда именно мы фиксируем эти события, а зависит только от того, за какой промежуток времени эти опоздания установлены. В таком случае можно рассчитать интенсивность X постоянного потока рассматриваемых нами случайных событий, когда возврат произошел с запаздыванием:

Этой характеристики вполне достаточно, чтобы полностью охарактеризовать простейший поток случайных событий - опо­зданий с возвратом кредита или погашения векселей — и рас­считывать характеристики риска.

Например, функция F(f) распределения непрерывной слу­чайной величины 7 продолжительности времени запаздывания с возвратом кредита задает вероятность того, что момент возвра­та кредита с запаздыванием наступит не позднее фиксированной величины t. Эта функция имеет вид:

F(t)=P(t< t) = 1-e -'"'.

Это неубывающая функция своего аргумента с параметром А. интенсивности потока запаздываний. Следовательно, чем боль­ше значение величины t продолжительности запаздывания, тем

Глава 3. Управление стохастическими рисками

меньше вероятность невозврата к этому сроку при заданной ве­личине X. Например, вероятность запаздывания с возвратом средств не позднее среднего времени Т_ср запаздывания (то есть вероятность наступления Р(1 < Т_с )= F(T_C )= 1 - е'^ьт'

ср' - у ср >

та средств не позднее двукратного среднего времени запаздывания

будет равна Р(7 <2T_Cf=) F(2T_c/= 1 -е'^к'²=1 -e"²=0,865, а

через три средние продолжительности запаздывания средства бу­дут возвращены практически достоверно (P(t < ЗТ_С = 1 -_e-*-^iT» =l-_e-³ =0,950).

Итак, при запаздывании с возвратом кредитованных средств заимодатель несет убытки — отданные им в кредит средства не работают и не приносят дохода. Какими могут быть эти потери по величине? Пусть г* - процентная ставка наиболее выгодного размещения средств. Тогда, например, при средней задержке Т_ср времени погашения векселей на одной факторинговой операции кредитор потеряет г*Т_ср, а при номинале вексельного портфеля, обслуживаемого факторингом, равном N, эти потери составят ужеr*T_cpN.

Следовательно, с учетом риска несвоевременного возврата ставка кредитования должна быть скорректирована на «эффект задержки» в погашении векселей. Для этого следует банковскую ставку г₀ кредитования при нулевом риске увеличить на некото­рую долю от процентной ставки г* наиболее выгодного размеще­ния средств. Величину доли от процентной ставки/** определить пропорционально отношению величины среднего времени Т_ср задержки погашения векселей к среднему сроку кредитования (среднему сроку жизни векселей до погашения).

ГЛАВА 4

Не нашли, что искали? Воспользуйтесь поиском по сайту: