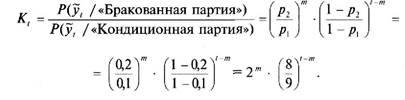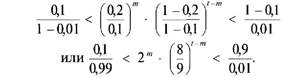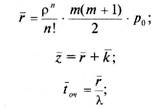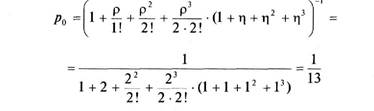|
|
ИСПОЛЬЗОВАНИЕ МАТЕМАТИЧЕСКИХМОДЕЛЕЙ И МЕТОДОВ ДЛЯ ОБОСНОВАНИЯ РИСКОВАННЫХ ПРЕДПРИНИМАТЕЛЬСКИХ РЕШЕНИЙ Определение оптимального размера выборки для принятия решения о назначении скидки с подписной цены журнала. Предприниматель, занимающийся изданием глянцевых журналов, решает вопрос об увеличении тиража журнала, поскольку это обещает дополнительную прибыль. Однако он понимает, что если спрос на журнал не увеличится, то дополнительный тираж — это чистые убытки. Для составления прогноза величины будущего дохода предприниматель может получить информацию о размере процента положительных ответов при помощи опроса не всех, а только некоторой части из бывших подписчиков журнала. Однако возник вопрос, насколько такая информация может быть точной. Мы достаточно хорошо понимаем, что вопрос о цене не отделим от вопроса о качестве, причем чем выше качество информации, тем выше ее цена. Следовательно, необходимо было оптимизировать соотношение цены и качества. Предприниматель решил произвести случайную выборку 50 имен из рассылочной ведомости, получить ответы от подписчиков и на основе полученных положительных ответов оценить будущее количество подписчиков. На основе опыта подобных действий в прошлом наш предприниматель сделал предположение — выдвинул гипотезы — о проценте возможных положительных ответов. Пусть, например, он считает, что процент ответов будет между 1 и 5, и при этом нет причин считать, что возможность получения какого-либо конкретного процента из представленных более вероятно, чем другого. При таком предположении каждому возможному (гипотетическому) проценту ответов соответствует одинаковая вероятность, равная, согласно классическому определению, 1/5. Обозначим через Н\ Н2, Я3, Н4, Я5 гипотезы о том, что процент положительных ответов составит 1, 2, 3, 4 и 5 соответственно. Тогда в этих обозначениях априорные вероятности гипотез составят Р(Н\) = Р{Н2) = Р(#з) = Р(^4) = P(Hs) = 0,2. После рассылки предложений клиентам число положительных ответов будет дискретной случайной величиной, подчиняющейся закону Глава 3. Управление стохастическими рисками редких событий — распределению Пуассона. Напомним, что вероятностный ряд или ряд распределения Пуассона задается формулой:
где а — математическое ожидание случайной величины у; к = 0, 1, 2, 3, ... — возможные значения, которые может принимать случайная величина у. Случайное число у положительных ответов будет иметь среднее значение (математическое ожидание) а такой величины, которая, как мы помним, определяется выражением а = пр, причем в нашем примере п — 50, а вероятность р успеха диктуется величиной предполагаемого процента успеха. А теперь примем во внимание, что одно и то же значение к рассматриваемая нами случайная величина может принять при разных значениях параметра а, то есть своего математического ожидания. Таким образом, можно получить, например, три положительных ответа и в том случае, когда истинный процент желающих возобновить подписку на журнал по льготным условиям равен 1%, и в том случае, если этот процент будет равен 2, 3, 4 или 5. Только вероятности Р(у"''и) этих условных событий окажутся разными: чем ближе значение к возможного значения случайной величины к ее среднему значению а, тем, как правило, выше значение вероятности Р(?-%)и наоборот. Для рассматриваемых нами гипотез Н\ Н2, Н^, Н4, Н5 о проценте положительных ответов величины вероятностей успеха составят^, = 0,01,р2- 0,02, р3= 0,03,р4 - 0,04 ир5= 0,05 соответственно. Следовательно, математическое ожидание случайной величины у числа положительных ответов для первой гипотезы Нх составит величину а, = 50 • 0,01 = 0,5. Аналогично можно подчитать средние значения чисел положительных ответов для остальных гипотез: «2=1,0, а3—1,5, й4=2,0, а5= 2,5. Для вычислений вероятностей Р(у =у к) рядараспределения Пуассона, как мы уже отмечали, удобно использовать функцию ПУАССОН(х; среднее; ...) пакета Microsoft Excel. С использованием этой компьютерной программы была вычислена зависимость между случайным числом подписавшихся (возможные результаты выборки) и гипотетическим процентом ответов. Услов- Риск -менеджмент ные вероятности Р(у=%) возможных значений числа к полученных положительных ответов для различных гипотетических значений процентов истинных положительных ответов представлены в табл. 3.4. Т а б л и ц а 3.4
Условные вероятности Р(у=к/„ ) возможных значений числа к полученных положительных ответов для различных гипотетических значений процентов истинных положительных ответов. Проанализируем данные, например, четвертой строки табл. 3.4. Для удобства ее значения оттенены. Видно, что ровно три (значение к=3) положительных ответа из 50 на предложение возобновить подписку на льготных условиях при истинности первой гипотезы (один процент положительных ответов) будут получены с вероятностью 0,013; а при истинности других гипотез — Н2,Н2,Н4,Н> — вероятность этого же числа успехов составит 0,061; 0,126; 0,180 и 0,214 соответственно. Глава 3. Управление стохастическими рисками Но для целей принятия решения на рискованную операцию нашему предпринимателю нужно знать не те вероятности, которые представлены в табл. 3.4, а другие — апостериорные вероятности Р("'у=к) ИСТИННОСТИ гипотез при получении того или иного из возможных значений к случайной величины у. Их легко определить, воспользовавшись формулами условной и полной вероятности. Напомним эти формулы: Р(А/В) = — -, Р(В) ф 0 - формула условной вероятности; Р(А) = "£Р(А вк) Р(Вк— формула полной вероятности. к Следуя этим формулам, для вычисления вероятностей Р(и'4=к) нужно вначале найти вероятности P(Hi(y=4i)) = Р(Н/)-Р(>'=к/н)и Р(у -к), а затем уже вычислить требуемые вероятности по формулам:
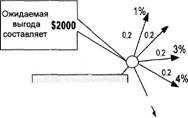
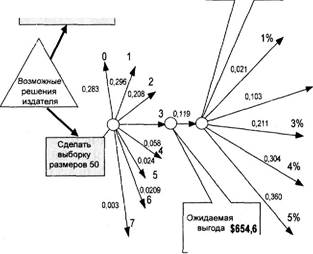
Рассчитаем, например, апостериорные вероятности Р(н у-^) для случая, когда на 50 разосланных предложений пришло ровно 3 ответа с намерением возобновить подписку по специальной цене. Вначале вычислим совместные вероятности Р(Я1 • (у = 3)) = = Р(Н,.) • Р(*'ън) наступления каждого из гипотетических событий — процентов ответов и события — результата, состоящего в том, что у = 3. Вспомним, что вероятности Р(Я,), Р(Нг)Р(Н3). Р( Я ДР( Я, гипотетических событий-процентов ответов равны 0,2. Следовательно, например, искомая вероятность совместного события Р(Я, • (у = 3)) составит величину Р(Н[ • (у = 3)) = = Р(Я,) • Р(^3д) =0,2 • 0,013 = 0,0026. Аналогично получаем: Р(Н• (у = 3)) =0,2 • 0,061 = 0,0122; Р(Н3 • (у = 3)) = 0,2 • 0,126 = = 0,0252; Р(Н• (у=3))=0,2 • 0,180 = 0,0361 и P(HS • (у = 3)) = 0,2 • 0,214 = 0,0428. Сума полученных совместных вероятностей дает полную вероятность Р(у = 3), которая получается равной 0,1187. В результате чего апостериорные вероятности Р(н'/~^) = Р(Н„)Р(^ ) /Н ч =----------------- —— будут соответственно равны: Р( '/~^) = Р(у =3) Риск-менеджмент =0,0026/0,1187 = 0,021; />("' Р.3)= 0,0122/0,1187= 0,103; Р("< f.3) = = 0,0252/0,1187 = 0,211; /'("^=0,0361/0,1187 = 0,304 и P("^J = = 0,0428/0,1187 = 0,360. Таким образом, как это следует из расчетов, вероятность увеличения числа подписчиков на журнал по специальной цене на 1% при условии, что из 50-ти разосланных предложений ровно 3 содержало положительный ответ, равна 0,021, хотя априорная вероятность этой гипотезы была 0,2. Соответствующие апостериорные вероятности увеличения числа подписчиков ровно на 2%, 3%, 4% и 5% по результатам проведенных нами вероятностных расчетов составили 0,103, 0,211, 0,304 и 0,360 соответственно (в то время как априорные вероятности всех этих событий были одинаковыми и равнялись 0,2). На рис. 3.8 представлено дерево возможных событий для случая сравнения этой стратегии и стратегии предварительной рассылки 50 предложений продолжить подписку по специальной цене, причем на этом дереве в развернутом виде представлены события только для случая, когда получено 3 положительных ответа из 50. Апостериорные вероятности гипотез для этого случая нами уже вычислены, а их значения проставлены возле стрелок, изображающих случайные исходы рассылки предложений подписчикам. Средняя величина ожидаемой прибыли при вычисленных значениях апостериорных вероятностей (для 3 положительных ответов из 50) составляет $5513. Чтобы получить это значение, потребовалось, как обычно, умножить значение апостериорной вероятности для каждой из гипотез на соответствующее этой гипотезе значение дохода (положительного или отрицательного) и полученные значения всех произведений сложить. Для исхода «3 положительных ответа из 50» величина среднего дохода представлена на рис. 3.8 в вынесенном прямоугольнике. Как видим, если предприниматель решится на рассылку предложений подписчикам и получит ровно 3 положительных ответа, то ожидаемая прибыль почти в 2,8 раза превысит то ее значение, которое было вычислено для случая, когда издатель хотел делать предложение о спеццене без предварительного сбора информации. До проведения рассылки, конечно, нельзя предсказать ее результатов. Однако можно рассчитать ожидаемую выгодность для каждого возможного числа положительных ответов. Значения априорных вероятностей для всех возможных исходов рассылки Глава 3. Управление стохастическими рисками
спеццене без гсоедварительного сбора информации Ожидаемая выгода $5513 составляет $2000 Рис. 3.8. Дерево возможных событий для сравнения стратегий с предварительной рассылки 50 предложений продолжить подписку по специальной цене (развернут исход для случая 3 положительных ответа из 50) (в том числе и для к = 3) представлены в табл. 3.5. Рассмотрены только значения к от 0 до 7, поскольку вероятность получения значений, больших чем 7, очень мала. Далее обычным порядком используем полученные апостериорные вероятности, установленные для каждого успешного результата к выборки, для того чтобы определить значение общей ожидаемой выгодности действия «Сделать выборку размером 50». Например, учитывая, что значение полной вероятности Р(у = 3) рассматриваемого нами исхода равно 0,1187 (на рис. 3.8 проставлено значение 0,119), то ожидаемая величина дохода при получении ровно трех положительных ответов после рассылки 50 предложений составит $654,6. Риск-менеджмент Т а б л и ц а 3.5 Значения априорных вероятностей для возможных исходов рассылки предложений подписчикам
В табл. 3.6 представлены значения условных величин дохода для каждого из возможных исходов случайной выборки объемом 50 человек, полные вероятности для этих исходов и частные величины полных ожидаемых доходов для них. Видно, что условный (и, следовательно, частный полный) доход от выборки для нулевого исхода — ни один из опрошенных не ответил положительно на предложение возобновить подписку по специальной цене — отрицательный. Но если есть хотя бы один положительный ответ, это уже дает положительный эффект, степень которого определяется величиной полной вероятности исхода. Например, исход к = 7 приносит самую большую условную величину дохода, равную $8545, однако из-за того, что полная вероятность Р(у = 7) такого исхода составляет всего лишь 0,0028; частная величина полных ожидаемых доходов для него будет всего только $24,3. Т а б л и ц а 3.6 Значения условных величин дохода для каждого из возможных исходов случайной выборки
Глава 3. Управление стохастическими рисками Продолжение табл. 3.6
В результате сложения величин этих частных ожидаемых выигрышей получается общая ожидаемая выгодность рассылки предложений 50 прежним подписчикам с последующим анализом полученных положительных ответов. Она составляет чуть больше $1990. Следовательно, ожидаемая ценность информации, полученной в ходе рассылки предложений 50 прежним подписчикам, будет равна разности между этим результатом и ожидаемыми последствиями действия «Делать предложение». При тех исходных данных, которыми мы пользовались, эта ценность отрицательна $1990 — $ 2000= —$10, то есть собирать информацию при данных условиях получается невыгодно. При этом мы даже не учитывали дополнительные затраты на проведение самой случайной выборки респондентов для рассылки им предложений, а это всегда нужно делать, чтобы не исказить картину исхода. Тем не менее склонный к риску предприниматель может пойти на решение сделать выборку, поскольку получение хотя бы одного положительного ответа может дать ценную информацию для получения более точного прогноза будущих доходов от подобной предпринимательской акции. К тому же необходимо иметь в виду, что значения вероятностей исходов существенно зависят от объема выборки. Поэтому представляется целесообразным подсчитать по предложенной' нами схеме ожидаемую полную выгоду от организации сбора информации для случайных выборок разного объема. После этого можно будет сопоставить полученные результаты и окончательно определить оптимальный размер выборки, приносящий максимальный ожидаемый суммарный доход. Риск -менеджмент Контроль качества продукции методом последовательного анализа (Вальда). На выходе производственной линии производится контроль качества готовой продукции. С целью экономии затрат времени и средств на контроль изделия для контроля отбирают из готовой партии случайным образом. После этого проводится тщательный контроль изделия. По мере накопления информации о результатах контроля формируется решение о качестве продукции во всей произведенной партии по методу последовательного анализа. Предприятие будет работать успешно и приносить прибыль только в том случае, если доля брака в партии выпущенной продукции не превышает 10% от общего числа изделий в каждой партии. Поэтому такое значение принято в качестве критерия оценки качества всей партии готовой продукции. Одновременно принято решение считать, что партия «бракованная», если доля некондиционных изделий в ней не менее 20%. Учитывая возможность совершения ошибок первого и второго рода при контроле, а также тяжести последствий от каждой из ошибок, были назначены предельные значения вероятностей указанных ошибок. Предельное значение вероятности а совершения ошибки, в результате которой бракуется кондиционная продукция, установлено равным 0,01, а вероятность р пропуска бракованного изделия при контроле (изделие ошибочно принято за кондиционное) ограничена величиной 0,1. Контроль и выработка решения о состоянии всей партии готовых изделий по методу последовательного анализа организуются на основе частных выводов после каждого очередного проведенного испытания изделия. Предполагается, что после каждого очередного контроля возможны три основополагающих вывода: завершить контроль и принять всю партию, проконтролировать еще одно изделие из готовой партии, завершить контроль и забраковать всю партию. Оказывается, что обозначенные нами частные решения после каждого шага контроля будут адекватными, а вероятности ошибок первого и второго рода не выйдут за пределы установленных для них границ, если руководствоваться критерием К, вида: Р(у, /«Бракованная партия») Р{у, /«Кондиционная партия»)' Глава 3. Управление стохастическими рисками где у, - случайное число бракованных изделий, выявленных к шагу /; Р(уг = /«/«Бракованная партия» — условная вероятность того, что случайное число бракованных изделий, выявленных к шагу /, будет равно т при условии, что партия бракованная; Р(у, = т / « Кондиционная партия» — условная вероятность того, что случайное число бракованных изделий, выявленных к шагу /, будет равно т при условии, что партия кондиционная. Чтобы определить обозначенные условные вероятности, входящие в выражение для критерия К,, в количественной форме, необходимо учесть, что, согласно принятому предпринимателем решению, партия считается кондиционной, если доля р, брака не выше 0,1 (установлена в размере 10%), а в бракованной партии доля/?2брака не ниже 0,2 (то есть не менее 20%). Дискретная случайная величина у, при этом оказывается распределенной по биномиальному закону. Напомним, что основой биномиального распределения является следующая схема. В совершенно одинаковых условиях — одна и та же доля р бракованных изделий в большой партии — проводится независимый контроль п одинаковых изделий. Результат контроля случайный: с вероятностью^ под контроль подпадает именно бракованное изделие, а с вероятностью 1 —р бракованное изделие не попадает в число контролируемых. Итак, поскольку партия готовых изделий достаточно большая, вероятность р от изделия к изделию не меняется. Фиксируется число т изделий, которые выявлены как бракованные. Это число будет одной из возможных реализаций случайной величины, которая может принимать значения от 0 до п. Вероятность того, что дискретная случайная величина у примет значение, равное т, за- п\ дается выражением вида Р(у=т)-------------- :------- р'"(1 - Р)" т или т\{п - ту. кратко - Р(у = т) =С'У"(1 - /?)""', где С"' =----------------------- число сочетаний из п по т. т\{п - т)\ Таким образом, за t шагов (число проведенных испытаний) получаем: Р(у, = т /«Бракованная партия») = С,'" • р'" • (1 -/>,)'"", Р(уп =//«Кондиционная партия») = С,'" • р"' • (1 - />,)'"". Риск-менеджмент После каждого очередного шага контроля формируются основополагающие выводы по схеме: ' < К, <------ 1 - а а сделать еще одно измерение;
Р 1 -а > К, принять кондиционную партию;
л, >
а забраковать всю партию. Вероятности ошибок первого и второго рода соответственно равны: а = 0,01, 0 = 0,1. Запишем выражение для критерия К, в наших условиях:
1еперь сформируем границы распознавания ситуации в зависимости от достигнутого к шагу t результата т числа идентифицированных бракованных изделий. Запишем формальное выражение для основополагающего вывода: «сделать еще одно измерение». Для наших исходных данных получаем:
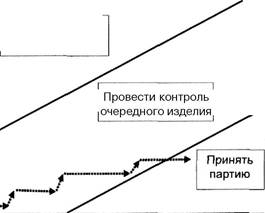
Проведем допустимое преобразование (логарифмирование): [/л0,1 -/«0,99] < [т • lnl + (t - т) • (/«8 - 1пЩ < [М),9 - /«0,01] или -2,293 < (0,693 + 0,118) • т -0,118 •/< 4,5. Глава 3. Управление стохастическими рисками Из последнего неравенства получаем границы зависимости между т и t. 0,145 • t - 2,82 </и< 0,145 • t + 5,55. Границы выполнения двух представленных в выражении неравенств — это прямые линии в системе координат t и т.Если изобразить их графически, то удобно будет делать частные выводы и одновременно документировать результаты вынесения решений. На рис. 3.9 представлена система координат (t, m) и разделяющие границы областей для формирования частных выводов. По мере проведения измерений t и фиксации числа m выявленных бракованных изделий результаты можно изображать графически в виде траектории процесса контроля. Такая траектория изображена на рис. 3.9 последовательностью пунктирных стрелок. Траектория процесса контроля начинается из точки (0; 0), что соответствует ситуации «ни одного изделия не проконтролировано и, следовательно, ни одного бракованного не выявлено». Если проведено одно измерение и брак не обнаружен, траектория процесса выходит в точку (1; 0).
1 4 7 10 13 16 19 22 25 28 31 34 37 40 43 46 49 52 55 58 61 64 67 70 Числопроведенных испытаний Рис. 3.9. Разделяющие границы областей для формирования частных выводов Риск -менеджмент Если проводить измерения и дальше и при этом не будут выявлены бракованные изделия, то траектория процесса будет продолжать развиваться вдоль оси t. Если на каком-то шаге процесса контроля будет обнаружено первое бракованное изделие, на этом шаге траектория процесса контроля изменит угол движения на 45 градусов. И так будет всякий раз, как только будет обнаруживаться брак. В результате траектория превращается в ломаную линию, устремленную в общем случае вправо и вверх. Скорость подъема траектории вверх зависит от частоты обнаружения бракованных изделий среди проконтролированных. И если брак выявляется достаточно часто, то траектория процесса устремляется в направлении северо-западной части системы координат (t, т). Эта часть ограничена снизу линией т = 0,145 • t + 5,55 и образует область значений числа t проведенных испытаний из числа т выявленных бракованных изделий, при попадании в которую вся партия должна быть забракована. Напротив, если число бракованных изделий в партии готовой продукции незначительное, траектория процесса редко будет изламываться вверх. При этом, рано или поздно, она пересечет границу, задаваемую уравнением т =0,145 - / -2,82, которая отсекает юго-восточную часть области значений характеристик / и т, которая соответствует базовому решению: «Принять всю партию». Траектория процесса контроля, соответствующая именно такому случаю, и отображена на рис. 3.9. Несмотря на то, что все же возможно принятие ошибочного решения, вероятности аир ошибок первого и второго рода не выйдут за пределы установленных для них пороговых значений. Кроме того, как показывают исследования, для обеспечения подобного же качества контроля по методу Неймана-Пирсона потребуется в среднем вдвое большая по объему выборка, чем та, которую придется осуществить по методу последовательного анализа Вальда. И, следовательно, затраты на проведение контроля качества произведенной продукции будут в среднем вдвое ниже. Предпринимательская деятельность по предоставлению услуг. Для коммерческой и иной подобной предпринимательской деятельности адекватными моделями оценки риска могут служить модели со случайными потоками событий. При этом события следует рассматривать как факты выполнения взаимных обязательств между сторонами по объемам и по срокам. Наиболее Глава 3. Управление стохастическими рисками широко используют модели с так называемыми простейшими потоками событий. В простейшем потоке все наступающие события одинаковы, однако времена их появления — случайные, подчиняющиеся показательному закону распределения (свойство «без последействия»). При этом для простейшего потока характерно, что параметр показательного закона распределения — среднее время между событиями — постоянен во времени (свойство стационарности), а события появляются поодиночке (свойство ординарности). Примером простейшего потока может служить поток автомобилей, прибывающих на автозаправочную станцию, поток телефонных звонков, поступающих в центр мобильной связи, и т.п. Для анализа разнообразных видов предпринимательской деятельности, в рамках которых циркулируют простейшие потоки событий, можно с успехом применять мощный математический аппарат анализа так называемых Марковских процессов. В рамках этого подхода, например, разработаны большинство моделей систем массового обслуживания (СМО). Но не всегда потоки событий могут считаться простейшими. Например, как в предпринимательской деятельности, так и в быту, людям приходится совершать разнообразные платежи. Потоки платежей для банка и для потребителей часто оказываются случайными в силу случайных моментов времени их осуществления и случайных величин платежей. Например, таковыми являются потоки платежей за предоставление коммунальных услуг, за тепло и электроэнергию — ведь редко кто платит за все эти услуги в строго определенный день. При этом размеры платежей также могут быть случайными, в том числе и по причине их несоответствия объему и качеству предоставленных услуг: кое-кто не доплачивает, некоторые, по ошибке — переплачивают. Другой пример случайных платежей, с которым с недавних пор (после вступления в силу закона об обязательном страховании автогражданской ответственности) приходится сталкиваться значительному числу людей, — это выплаты страховых сумм за повреждение личного или общественного автотранспорта. Продажа бензина на автозаправочной станции (АЗС). Во времена «начала перестройки» в России АЗС представляли собой достаточно громоздкие технические сооружения, как, впрочем, многие сооружения того времени. Считалось, что это позволяет экономить площади отводимых под них участков земли. Пока Риск -менеджмент автотранспорта в городе было сравнительно мало и он был, как правило, государственным, с этим можно было как-то мириться. Однако быстрый рост количества частных автомобилей в начале 90-х годов прошлого столетия, например в Москве, сделал ситуацию с автозаправками критической. Летом по пятницам, когда в конце рабочего дня тысячи москвичей устремлялись на дачные участки, к АЗС выстраивались километровые очереди. Решить эту проблему в короткие сроки, превратить заправку большого числа автомашин в событие подстать покупки газеты, можно было только создавая много малых АЗС, достаточно плотно размещенных по всей территории города. Ведь крупные АЗС просто не было возможности разместить в перенаселенном городе. Это еще одна причина, почему их и было крайне недостаточно. В настоящее время АЗС представляют собой небольшие площадки с оборудованием, имеющим для розлива горюче-смазочных материалов не более 3—5 колонок. При ожидании своей очереди для заправки прибывающие автомашины располагаются на небольших площадках вблизи АЗС, позволяющих разместить также небольшое число автомашин, как правило, — не более пяти. Если считать поток прибывающих на подобную АЗС автомашин случайным простейшим, то ее работу можно с успехом моделировать как случайный процесс функционирования ««-канальной СМО с ограниченной очередью». При моделировании работы подобной СМО используем следующие обозначения: п — число заправочных колонок (число каналов обслуживания); So, Sj, S2, S3, S4, ..., Sn — число занятых колонок (возможные «состояния СМО»); т — число мест для автомашин на площадке ожидания (число мест в очереди); X — интенсивность потока прибывающих на АЗС автомашин (интенсивность входного потока заявок); 'оесл - среднее время заправки одного автомобиля (обслуживания одной заявки). При таких обозначениях сразу вычисляют параметры работы подобной СМО: ц = 1АобС1 — интенсивность потока обслуживания; Глава 3. Управление стохастическими рисками X р =------- «степень загруженности» канала; И р X т| = — =-------- отношение величины р к числу каналов обслу- п n\i живания («распределенная степень загруженности» СМО). В качестве главных характеристик эффективности работы АЗС, как «n-канальной СМО с ограниченной очередью», были приняты: А - абсолютная пропускная способность (среднее число автомобилей, обслуживаемое АЗС в единицу времени); Q - относительная пропускная способность (вероятность заправки прибывшего автомобиля); очевидно, что Q = АД; Ротк — вероятность отказа в обслуживании, то есть вероятность того, что прибывший автомобиль не будет обслужен и покинет данную АЗС, поскольку все заправочные колонки и все места на площадке ожидания заняты; следовательно, Ротк= 1 — Q; к — среднее число занятых заправочных колонок (каналов обслуживания); z — среднее число автомобилей, «связанных» с рассматриваемой АЗС, то есть заправляющихся или находящихся в очереди; г - среднее число автомобилей (заявок) в очереди; to** - среднее время пребывания автомобиля на АЗС (в очереди или под обслуживанием); tт — среднее время ожидания заправки, если заняты все колонки (среднее время пребывания заявки в очереди). Эти характеристики вычисляют по следующим формулам: Г, Р Р2 Р"ря+| 1-тгУ1 * рп = 1 +— + - + ... + - +----------------- финальная веро- ^ 1! 2! п\ п • п\ [ -ц) ятность P(S0) свободного состояния («простоя») СМО; если г| — 1, то в последнем слагаемом в скобках нужно в числителе дроби разложить (1 — r|m) на произведение (1 — г|)(1 + ц + г\2 + + г)3 + ... + г)т|) и дробь сократить, после чего от нее останется просто сомножитель (1 + л + ц1 + г|3+ ... + r|m_l); Рк , , рк = — • _£>„для I < к < п к\ и Риск-менеджмент
P Pmr = —----- j ■ PO
P„M,r-\) -Ц ' /7ш</--1)>Для l^^<w - ос- тальные финальные вероятности; A = X(l - pn+m)'i Q = 1~Рп+т'уРотк=Рп+т —вероятность отказа в обслуживании, то есть вероятность того, что в момент поступления заявки все-каналы обслуживания и все места в очереди заня-ты, -поэтому поступившая заявка не будет обслужена и покинет
V / р Т W г =---------- —--——-!—, ДЛЯ ЛЮбОГО г) < 1 ИЛИ г\ > 1, пп\ (1-л) а для т) = 1 выражение для среднего числа заявок/- в очереди определяют на основании предельного перехода и получают выражение:
Рассчитаем указанные финальные вероятности и характеристики эффективности АЗС для следующих исходных данных: на АЗС имеются две заправочные колонки (п = 2); на площадке ожидание могут располагаться четыре автомашины (пг = 4); поток автомашин, прибывающих на АЗС, имеет интенсивность \=1 автомашина/мин; среднее время обслуживания автомашины to6cl = 2 мин. На основании этих исходных данных вычисляем по представленным формулам: У^ба
1/2 = 0,5 автомашина/мин; р = -=2;г| = ^=1. ц п
финальная вероятность/?/ того, что на АЗС занята только одна из двух имеющихся колонок равна В = = ■$ =~2 1 =—' остальные финальные вероятности р2, Рз, Р4, Ps и р6 также 2 оказываются равными —. Через полученные финальные вероятности находим характеристики эффективности работы АЗС: Ротк P n+m =p2+4 =Рб--------- относительная пропускная способность АЗС составляет, следовательно, величину Q = 1 - Ротк= - или приблизительно 85% всех прибивающих на АЗС автомобилей, что вполне удовлетворительно; в абсолютном выражении (показатель абсолютной пропускной способности) это составляет величину А = A.Q = - * 0,85 машины/мин. Именно эти, обслуженные автомашины принесут владельцу АЗС прибыль. Кроме того, можно утверждать, что в среднем на данной АЗС А 22 постоянно задействованы к = р(1 - р„) = - = - ~ 1,69 колонки М 13 161 Риск -менеджмент
но находятся в среднем ли! О-л) 2! ■—----- -■—«1,54машины. Иными словами, емкость стоянки 2 13 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
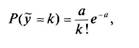
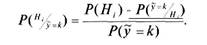
 Делать предложение о
Делать предложение о