СУБЪЕКТИВНЫЕ КРИТЕРИИ ОЦЕНКИ СТОХАСТИЧЕСКОГО РИСКА

Но что, если и это не помогло нашему предпринимателю оп­ределиться в выборе? Исследования, например, показывают, что для каждой величины дисперсии результатов существует вполне определенная компенсирующая величина среднего результата, делающая вариант решения для предпринимателя вполне при­влекательным. Другими словами, как мы уже отмечали, пред­приниматель может пойти на риск не оттого, что риск для него «привлекателен» (имеет положительную ценность), а потому,

Риск-менеджмент

что он рассчитывает на получение более высокого положитель­ного эффекта. Так вот, в подобных ситуациях ему уже просто не­обходимо учесть индивидуальные особенности оценки полезно­сти значений результатов и субъективного восприятия риска.

Приходится не ограничиваться использованием только объ­ективных характеристик распределения результата. Использова­ние объективный показатель для учета риска имеет очень суще­ственный недостаток — не существует нормативной теории, ко­торая позволяла бы четко указать, когда и какой (какие) объективный показатель адекватно отражает предпочтения ЛПР в ситуации выбора в условиях стохастической неопределенно­сти. Этого недостатка лишены аксиоматические методы по­строения функции выбора наилучшей альтернативы, которые не только дают теоретическую основу для качественного учета осо­бенностей отношения ЛПР к вероятностным распределениям на множестве результатов, но и позволяют дать им обоснованную количественную оценку в виде функции полезности.

В теории ожидаемой полезности определяют функцию по­лезности и(у) случайных результатов у, математическое ожида­ние которой полностью определяет предпочтения ЛПР на лоте­реях с учетом индивидуального отношения к риску.

Модель ожидаемой полезности (МОП) - наиболее старый вариант нормативного подхода к принятию решений. Считают, что истоки модельных построений принятия решений восходят к Блезу Паскалю, который предложил тактику выбора в азарт­ных играх: выбирай ту альтернативу, при которой будет макси­мальным произведение возможного выигрыша на его вероят­ность. Затем эту идею подхватили и начали активно разрабаты­вать Д. Бернулли, а затем и П. Лаплас. Однако совершенную форму, пригодную для практического использования ему прида­ли Дж. фон Нейман и О. Моргенштерн (1947 г.) и А. Эдварде (1954 г.). Термин «полезность» был обоснован Д. Бернулли в 1738 г., когда он дал схему соотношения богатства и полезности выигрываемых денег. Л. Сэвидж в 1954 г. создал теорию, в кото­рой допускались неожиданные субъективные альтернативы. Ро­дилось понятие субъективной вероятности. Было введено поня­тие субъективной ожидаемой ценности. С тех пор это понятие стало использоваться наравне с понятием объективной величи­ны исхода.

Глава 3. Управление стохастическими рисками

Обозначим функцию полезности через и(у). Согласно аксио­матической теории полезности отношение предпочтения на множестве альтернатив а моделируется с использованием мате­матического ожидания М[и(у(а))] функции полезности для этих альтернатив:

а, \~ а₂^М[и(у(а,))] > М[и(у(а₂))] .

Другими словами, если функция полезности задана, то по­лезность произвольной лотереи на результатах у лотереи опреде­ляется ожидаемой полезностью результатов этой лотереи. В ча­стности, одна из наиболее известных функций полезности — функция Бернулли, задающая полезность определенных коли­честв денег, получаемых в ходе случайной реализации исходов.

Теперь о практических приложениях функции полезности для предпринимательства. Так, наиболее известны две функции полезности денег. Одна из них — квадратичная функция полез­ности с положительными параметрами (функция полезности фон Неймана и О. Моргенштерна), задаваемая выражением и(у) = ау -р^².Разумеется, рассматривается только восходящая ветвь на неотрицательных значениях результата у. Отмечается, что широкое ее использование объясняется теоремой Нейма­на—Моргенштерна о том, что при определенных естественных допущениях экономическое поведение направлено на максими­зацию ожидаемого значения функции полезности. Другая, не менее распространенная - это логарифмическая функция по­лезности: и(у) = log_a у, для а > 0.

Несколько иной подход к учету субъективной стороны выбо­ра предлагают приверженцы теории проспектов — это предста­вители когнитивной психологии, которая более всего использует постулаты и представления экономики и математики, — реко­мендуют наилучший исход выбирать на основе полезности ре­зультата для этого исхода, умноженной на вес результата, а не на вероятность.

К такому выводу авторы теории проспектов пришли, анали­зируя субъективное восприятие величин вероятностей. Проил­люстрируем проявления искажений в восприятиях вероятностей на следующих известных примерах. Так, например, если обыч­ному человеку предъявить два упорядоченных набора из пяти чисел: (1, 2, 3, 4, 5) и (5, 1, 3, 5, 1), то он вряд ли сочтет равнове-

Риск-менеджмент

роятными эти последовательности, даже если они формируются путем равновероятного независимого выбора каждой очередной цифры из множеств {1, 2, 3, 4, 5}. Более того, около 70% испы­туемых обычно считают первую последовательность весьма ма­ловероятной в силу ее регулярности; то есть «степень сходства» регулярной последовательности с нерегулярной оценивается как весьма малая для случайностей.

По этой же причине при оценке вероятностей человек может игнорировать объемы выборок. Например, если вероятность не­кого элементарного события равна 0,5; то вероятности сложных событий типа «элементарное событие наступило 8 раз из 10» и «элементарное событие наступило 800 раз из 1000» часто вос­принимаются субъектом как одинаковые, хотя второе событие объективно менее вероятно. Далее. Оказывается, что если обыч­ного человека попросят оценить, например, техническую надеж­ность определенной марки легкового автомобиля, то, прежде чем вынести суждение, он припомнит поломки, возникавшие у подобных автомобилей у него самого, его друзей и знакомых. И если число поломок в известных ему случаях было значитель­ным, он вынесет суждение о весьма низкой вероятности безот­казной работы автомобиля данной марки.

Установлено также, что, стремясь к выравниванию вероят­ностей различных по правдоподобности событий, человек пере­оценивает объективную вероятность малоправдоподобных со­бытий и одновременно недооценивает вероятность очень прав­доподобных. Кроме того, выяснено, что человек гораздо выше оценивает вероятность выигрыша, чем вероятность проигрыша. Тверски и Канеман выделили несколько эффектов, проявляю­щихся при принятии решений [55]:

>-«эффект определенности» — люди переоценивают однознач­ные исходы по сравнению с высоко вероятными, они ста­бильно предпочитают $3000 наверняка лотерее ($4000; 0,8) или же лотерею ($3000; 0,9) лотерее ($6000; 0,45), а также лотерею ($6000; Ю-³) лотерее ($3000; 2 х 10"³),причем за­пись типа ($у; р) обозначает розыгрыш лотереи с исхода­ми $у и $0 (ноль долларов) с вероятностями р и 1 — р соот­ветственно; >-«эффект изоляции» — если выигрыш в лотерее — это уча­стие в другой лотерее, то вероятности первой и второй ло­терей человек не перемножает, он рассматривает лотереи

Глава 3. Управление стохастическими рисками

изолированно друг от друга, и в результате не работает ак­сиома свертывания;

>- при выборе люди учитывают не итоги выбора, а различие в состоянии до и после выбора;

>- имеет место качественный сдвиг при изменении вероят­ностей от 0,9 до 1,0 или от 0,0 до 0,1 по сравнению, напри­мер, с изменением с 0,5 до 0,6; другими словами, перехо­ды от невозможного к маловероятному или от высокой вероятности к абсолютной уверенности отличаются от любых других трансформаций в центре вероятностной шкалы;

>- наблюдается существенная асимметрия ^-образной функ­ции полезности для выигрышей и потерь. Отсюда: в ходе коммерческих и политических переговоров каждая из сто­рон более чувствительна к потерям, в результате чего ком­промиссные решения обеими сторонами воспринимают­ся как более проигрышные;

> • «эффект рамки», или влияние контекста на восприятие

альтернатив: если альтернативы сформулированы в тер­минах приобретений, то выбирают то, что безопаснее, на­дежнее и т.п., а если они сформулированы в терминах по­терь, то люди выбирают более рискованные решения (од­нако не все исследователи с этим согласны).

В итоге оказывается, что:

>- человек переоценивает объективную вероятность мало­правдоподобных событий и, одновременно, - недооце­нивает вероятность очень правдоподобных;

>• человек считает событие тем более вероятным, чем легче и быстрее можно запечатлеть в памяти примеры событий этого типа;

>• человек гораздо выше оценивает вероятность выигрыша, чем вероятность проигрыша;

> • при оценке вероятностей событий люди не принимают во

внимание объем выборки; >• независимые события человек часто рассматривает как за­висимые и др. Предложенная в теории проспектов функция весов пред­ставляет собой монотонную функцию от вероятностей, имею­щую указанные особенности. В том числе, низкие вероятности недооцениваются, средние и высокие переоцениваются, причем

Риск-менеджмент

последний эффект выражен сильнее, чем начальный. В области малых вероятностей веса по величине меньше, чем соответст­вующие им вероятности.

Один из авторов теории, А. Тверски, в соавторстве с Фоксом в 1995 г. показал, что в крайних областях вероятностей исходов (от 0,0 до 0,1 и от 0,9 до 1,0) вступают в действие два психологи­ческих эффекта. Один — оценка переходов от «невозможного в возможное», другой — из «возможного в наступающее наверня­ка». Они задействуют сдвиг по шкале «уверенность-неуверен­ность» в возможности исходов, а не по вероятностной шкале.

В работе других авторов (Миллер и Фогли, 1991) рассмотре-

1 2

ны иные диапазоны переходов: от - к , причем в последнем слу­чае событие переходит в категорию «субъективно возможного», а не только «неопределенного». В итоге вместо ожидаемой вели­чины выигрыша вводится представление о «мере полезности». В теории проспектов используется представление «весов реше­ний», которые не подчиняются аксиомам вероятностей и не должны интерпретироваться как «меры убежденности» (Шумей-кер, 1994 г.). «Веса решений» лишь монотонны по вероятностям и отражают общую привлекательность лотерей [55].

Принимая решения, люди демонстрируют искажения веро­ятностных оценок, зависимость выбора от контекста (например, «эффект рамки»), подмену частотного оценивания уверенно­стью и др. Для осуществления выбора между гипотезами или оценки вероятностей гипотез значительную роль играет процесс получения информации. Байесовский подход рассмотрел в сво­ей книге еще Ю. Козелецкий. Экологический (частотный) под­ход развил Гигеренцер (Gigerenzer). Иногда возникают ситуации принятия решений, в которых неопределенность относится к тем факторам, которые лишь предположительно (и в этом смыс­ле — «вероятно») могут повлиять на выбор субъекта. Например, характеристики альтернатив могут сулить большую или мень­шую вероятность тех или иных результатов для них, факторы ус­ловий (внутренних или внешних) влияют на восприятие той или иной информации. Особенно отличают влияние на вероятность вынесения того или иного условия факторов времени и последо­вательности.

Эффекты последовательности, или влияние порядка получения информации впервые были зафиксированы в 1946 г. С. Ашем.

Глава 3. Управление стохастическими рисками

Двум группам испытуемых Аш предъявлял один и тот же список свойств личности (зависть, упрямство, критиканство, импуль­сивность, трудолюбие, ум), но в прямом и обратном порядке. Оказалось, что действует эффект первичности — более сильное влияние на выносимое решение относительно свойств личности индивида производят те элементы, которые занимают первые три места в списке, практически независимо от того, что именно это за элементы. В ситуациях, когда люди знакомятся с противо­положным мнением, эффект первичности проявляется в том, что они остаются более подверженными влиянию первого впе­чатления, то есть первоначально полученных аргументов.

Иногда наоборот — именно последние из полученных сооб­щений оказывают наиболее сильное впечатление. Наблюдается эффект недавности. Особенно это заметно в ходе дебатов, пуб­личных разбирательств и т.п. Вопрос, каким выступать, таким образом, далеко не так прост. Оказывается, все зависит от вре­мени, через которое выносится решение. Если решение выно­сится сразу после окончания дебатов, то наиболее сильно прояв­ляется действие эффекта недавности, а если решение выносится спустя некоторое время после окончания дебатов, — эффект первичности. Об эффектах первичности и недавности необходи­мо постоянно помнить, принимая решения при подготовке и проведении деловых встреч и бесед, о которых мы будем еще го­ворить чуть позже.

Стоит заметить, что существование и характер проявления эффектов первичности и недавности хорошо усвоены адвоката­ми в судебной практике. Так, Н. Миллер и Д. Кэмпбелл прово­дили в середине 90-х годов XX в. деловую игру, в которой инсце­нировался судебный процесс, где истец требовал возмещения ущерба, нанесенного ложным обвинением. Восемь вариантов последовательности событий, которые рассматривались в этой деловой игре, схематично представлены на рис. 3.4 [55].

Испытуемые выносили вердикт, который и был принятием решения по делу. Существенным фактором оказалось время вы­несения этого приговора. Если о решении спрашивали через не­делю после прослушивания выступлений сторон, то проявлялся эффект первичности (3 и 4 варианты последовательности собы­тий). Если эта же неделя разделяла прослушивание информации обеих сторон, а решение выносилось сразу после прослушива­ния текстов последней из сторон, наблюдался эффект недавно-135

Риск -менеджмент

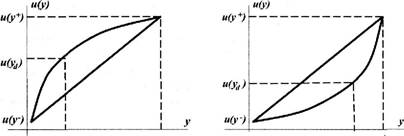
Вариант 1

Вариант 2

Вариант 3

Вариант 4

Вариант 5

Вариант 6

Вариант 7

Вариант 8

Рис. 3.4. Варианты последовательности событий, предлагаемые испытуемым в деловой игре

сти (последовательности 5 и 6). Две первые (1 и 2) и последние (7 и 8) схемы не испытывали влияния со стороны эффектов по­следовательности. Кроме того, оказалось, что в вариантах 5 и 6 испытуемые были в разной степени подвержены аргументам истца и ответчика. В частности, в варианте 5 испытуемые боль­ше могли рассказать о фактах, приведенных ответчиком (эффект недавности), а в варианте 6 в выигрыше оказывался истец, и ре­шение принималось в его пользу. Таким образом, если решение принималось сразу после последнего выступления, то преиму-

Глава 3. Управление стохастическими рисками

щества получал последний из выступавших. Сочетание факто­ров последовательности выступлений и времени, через которое следовало вынесение вердикта, может быть использовано не только самими выступающими, но и теми, кто ведет дискуссии или судебные разбирательства. Это «ведущий» имеет очень серь­езные рычаги управления принятием решения, давая выступаю­щим слово в определенном порядке и организуя необходимые последовательности перерывов в слушаниях.

Итак, желание или нежелание рисковать можно при необхо­димости внести в анализ предпочтительности альтернатив. На­пример, это можно сделать с использованием дерева решений. Для этого потребуется только построить функцию полезности для исходов рассматриваемого дерева событий.

Важным обстоятельством, позволяющим существенно облег­чить процедуру построения функции полезности, является то, что она аксиоматически задается с точностью до положительно­го линейного преобразования. Это означает, что если и(у) явля­ется функцией полезности случайного результата у, то все мно­жество {с • и(у) + с, к> 0} положительных линейных преобразо­ваний над значениями этой функции также дают функции полезности для оценки того же самого распределения результата у с той же самой психологической доминантой пользователя. То

есть любая функция из множества {к • и(у) + с, к > 0} упорядочи­вает альтернативы точно так же, как это делает исходная функ­ция полезности и(у). Следовательно, при построении функции полезности можно произвольно выбирать начало отсчета с и единицу измерения к. Поэтому чаще и удобнее выбирают нуле­вое начало отсчета и такую единицу измерения, чтобы функция полезности изменялась в пределах от нуля до единицы.

Заметим, что если предприниматель не склонен к риску, то для него индивидуальная функция полезности случайных значе­ний результата выпукла вверх. Проще всего это показать, ис­пользуя понятие базовой лотереи и достоверного эквивалента. Вообще в математической теории принятия решений лотереей называется пара (У, Р), где Y— {у,, У2,—,у_п} — множество возмож­ных значений случайного результата/, Р= (р_!ур₂,...,р_п) - веро­ятностное распределение на указанных результатах. В общем случае можно рассматривать лотереи с непрерывными значе­ниями результата, а также лотереи с векторными результатами и

Риск -менеджмент

составные лотереи (где результатом одной лотереи является дру­гая лотерея).

Психологические особенности человека таковы, что ему очень трудно сравнивать лотереи с большим числом выигрышей. Человеку гораздо проще иметь дело лишь с двумя исходами — наилучшим у⁺ и наихудшим у. Обычно человеку также доста­точно просто отвечать на вопросы типа: «За сколько вы соглас­ны отступиться от участия в ... <такой-то> лотерее?» или «Во сколько вы оцениваете ... <такую-то> лотерею, если вам предло­жат ее продать?» Кроме того, обычно предприниматель может достаточно уверенно ответить на вопросы, касающиеся сравне­ния по предпочтительности произвольного неслучайного ре­зультата у, не лучшего, но и не худшего, с так называемой базо­вой лотереей, в которой наилучший результат у⁺ получается с ве­роятностью р(у), а наихудший уг результат — с вероятностью 1 — р{у). Так вот, для оценки индивидуальной полезности и(у) конкретного неслучайного результата у, находящегося по пред­почтению между худшим у и лучшим у⁺, предприниматель дол­жен ответить на вопрос: «Какова, по вашему мнению, должна быть вероятность р(у) получения в базовой лотерее лучшего ре­зультата у⁺, чтобы вам лично было бы все равно — получить ли результат наверняка или участвовать в базовой лотерее с вероят­ностью р(у) для лучшего результата у⁺».

Предположим, например, что брокер в результате рискован­ной сделки может получить максимальный доход в размере $300 000 или потерять $100 000. Следовательно, для него у⁺= $300 000 и у- = -$100 000.

Предположим, что некто предлагает этому брокеру наверня­ка, то есть без всякого риска, доход в $100 000 (то есть в наших обозначениях неслучайный результат у= $100 000) или указать такую величину вероятности р(у) получения лучшего результата у⁺ = $300 000 с риском потерять $100 000, что ему будет все рав­но, получить ли $100 000 наверняка или участвовать в базовой лотерее ($300 000, р(у); -$100 000, 1 - р(у)). Предположим, бро­кер назвал свою оценку: при вероятности примерно 0,5 он не может отдать предпочтение ни получению наверняка $100 000, ни участию в базовой лотерее с исходами у⁺= $300 000 и у= -$100 000. Следовательно, полезность и($100 000) равна 0,5. На основе введенного нами понятия базовой лотереи можно сделать вывод о начале отсчета и единице измерения для функ-

Глава 3. Управление стохастическими рисками

ции полезности. Так, полезность наихудшего результата, оче­видно, нулевая, поскольку только при нулевой вероятности ЛПР будет все равно получить ли наихудший результат наверняка или участвовать в лотерее. Поэтому и()г) = 0. А вот полезность наи­лучшего результата равна единице, поскольку ЛПР пойдет на участие в лотерее против получения наилучшего результата на­верняка только в случае 100% гарантии успеха операции. Отсюда логически вытекает, что и{у⁺) = 1.

Однако вопрос о величине полезности можно поставить и по-другому: какой должна быть величина достоверно получае­мого результата y_d, чтобы для ЛПР было бы безразлично полу­чить ли результат y_d наверняка или участвовать в базовой лотерее с фиксированной вероятностью р(у) получения наилучшего ре­зультата. Предположим, мы выбрали базовую лотерею с характе­ристиками ($300 000; 0,5; -$100 000, 0,5), то есть зафиксировали вероятность р(у) на уровне 0,5. И спросили нашего брокера, на какой достоверно получаемый результат y_d он согласился бы, чтобы ему было бы безразлично получить ли его наверняка или участвовать в лотерее с равновероятными исходами и результа­тами $300 000 и -$100 000. Такой результат y_d называют досто­верным эквивалентом лотереи. Поскольку, по своей сути, обе формы вопросов эквивалентны, мы вправе ожидать, что брокер даст ответ: y_d = $100 000. Однако, как установлено психологами, вопрос о величине достоверного эквивалента базовой лотереи оказывается для большинства предпринимателей более ком­фортным.

Именно по величине детерминированного эквивалента дос­таточно просто судить о типе отношения ЛПР к стохастическому риску. И если оказывается, что детерминированный эквивалент y_d лотереи меньше математического ожидания М_у результатов лотереи, то ЛПР не склонно к риску, если y_d > М_у — склонно к риску, а если они равны - ЛПР безразлично к риску. Действи­тельно, так как для ЛПР, не склонного к риску, предпочтитель­нее получение среднего выигрыша наверняка, нежели участие в лотерее со случайными исходами, для него выполняется нера­венство: и(Му) > М[и(у)].

Аналогично можно показать, что функция полезности склонного к риску ЛПР строго выпукла вниз, а для безразлично­го к риску - линейна. На рис. 3.5 приведены функции полез­ности несклонного и склонного к риску ЛПР.

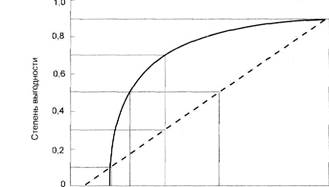
У У,/ У У* У

а) не склонный к риску б) склонный к риску

Рис. 3.5. Графики функций полезности не склонного и склонного к риску ЛПР

Рассмотрим процедуру построения функции полезности на интервале возможных значений результата коммерческой опера­ции для брокера, решающего вопрос о покупке руды. Ранее на­ми было установлено, что все возможные исходы этой коммер­ческой сделки лежат в диапазоне от - $100 000 до $300 000. Но брокер решил расширить диапазон возможных результатов для построения функции полезности. Он считает, что нужно при­нять во внимание возможные результаты со значениями от у- = -$ 110 000 до у⁺ = $500 000. Поэтому сразу же положим, что и(-$110 000) = 0 и и($500 000) = 1.

Далее предложим брокеру рассмотреть базовую лотерею с равновероятными исходами из диапазона [-$110 000; $500 000] и назвать ее достоверный эквивалент. Мы только что уже рассмат­ривали подобную задачу, поэтому для брокера она не представи­ла труда. Он назвал достоверный эквивалент в размере -$50 000. Поскольку полученному достоверному эквиваленту соответству­ет математическое ожидание функции полезности, равное 0,5, обозначим его достоверный эквивалент через y_0j5. Итак, у нас есть уже три точки, чтобы построить функцию полезности бро­кера, решающего вопрос о покупке руды по достаточно низкой цене в $5 за тонну. Это точки у = -$110 000, y₀,_s = -$50 000 и у⁺ = $500 000. Известны также значения величин полезности для них:

и(-$110 000) = 0, и(-$50 000) = 0,5 и и($500 000) = 1.

Величина yo,s= —$50 000 существенно меньше математиче­ского ожидания в лотерее с равновероятными исходами, равно-

Глава 3. Управление стохастическими рисками

му 0,5(-$110 000 + $500 000) = $305 000. Значит, наш брокер со­вершенно не склонен к риску.

Что делать дальше? Да то же, что мы только что делали! Толь­
ко в качестве исходных диапазонов для построения базовой ло­
тереи нужно будет рассмотреть два новых диапазона результатов:
[-$110 000; -$50 000] и [-$50 000; $500 000]. Эти диапазоны об­
разовались из исходного диапазона [—$110 000; $500 000] после
того, как мы разделили его точкой y₀j----- $50 000, соответствую­
щей полученному нами достоверному эквиваленту. Итак, спро­
сим теперь у нашего брокера: каков достоверный эквивалент для
лотереи с равновероятными исходами и диапазоном возможных
значений [-$110 000; у_в>5= -$50 000].

Напоминаем, что и(у = -$110 000) = 0 и и(у₀,5 = -$50 000) = = 0,5. Поэтому полученный достоверный эквивалент будет иметь полезность, равную 0,25. Поэтому обозначим его через Уо,25- Брокер подумал и ответил, что достоверным эквивалентом Уо^25 диапазона [у- = -$110 000; у₀,₅ = -$50 000] значений резуль­тата является примерно —$80 000. Затем, для второго диапазона он назвал в качестве значения для точки Уо,75 величину, равную примерно $30 000...$35 000. Остановились на цифре $33 000. В системе координат (у; и(у)) через пять полученных точек была проведена плавная кривая, вид которой представлен на рис. 3.6.

-100 О + 100 -³⁰⁰
Последствия, тыс. долл.
брокер, не желающий идти на риск
---------------------- брокер, нейтрально относящийся к риску

Рис. 3.6. Эмпирическая кривая функции полезности (выгодности) для брокера

Риск -менеджмент

Если кривая была точно построена, то значения выгоды можно использовать вместо действительных последствий. Ис­пользование подобной кривой позволяет осуществлять анализ дерева решений в направлении предотвращения риска, причем с большой точностью. И если кривая была точно построена, то значения выгоды можно использовать вместо действительных последствий.

Именно эту эмпирическую кривую и приняли за функцию полезности брокера, отражающую оценку его личной выгодно­сти в задаче о покупке руды. При необходимости можно доста­точно просто аппроксимировать полученную кривую одной из аналитических зависимостей. Наиболее часто для аппрокси­мации эмпирической функции полезности несклонного к рис­ку ЛПР используют экспоненциальную зависимость вида и(у) = а+ fie~^Uy+s>, параметры которой достаточно просто опреде­лить либо методом наименьших квадратов, либо — методом вы­равнивания [13].

Оценка возможных результатов является наиболее сложным практическим вопросом в анализе дерева решений. Для практи­ческого использования при принятии коммерческого решения брокер решил отразить координаты основных точек полученной эмпирической кривой выгоды в виде таблицы и затем приме­нить эти данные в дереве решений. Координаты основных точек эмпирической кривой представлены в табл. 3.3.

Т а б л и ц а 3.3 Координаты основных точек эмпирической кривой

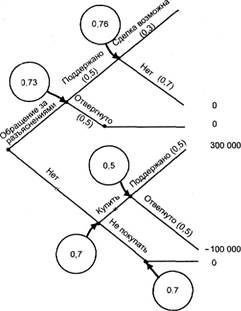
Изобразим на дереве решений брокера величины денежных сумм и соответствующие им значения их полезностей (выгодно-стей), взятые из данных табл. 3.3. Соответствующий фрагмент дерева решений брокера представлен на рис. 3.7.

Глава 3. Управление стохастическими рисками

0,9

0,7 0,7 0,9

0,1

0,7

Рис. 3.7. Дерево решений брокера с величинами денежных сумм и соответствующих им значениям их полезностей (выгодностей)

В кружках на рис. 3.7 проставлены математические ожида­ния полезностей для соответствующих ветвлений дерева. Срав­нение величин, помещенных в кружках, позволяет сделать вы­вод о том, что оптимальный вариант решения (с точки зрения брокера, не желающего идти на риск) диаметрально противопо­ложен варианту, являющемуся оптимальным с точки зрения рискующего брокера. Не имея дополнительной информации, брокер отвергает сделку. С другой стороны, как это следует из рис. 3.7, на котором изображено дерево решений, по максимуму ожидаемой полезности (величина 0,73 в кружке слева вверху вы­игрышным следует считать вариант обращения в правительство. Поэтому брокер, индивидуальная функция полезности которого явно свидетельствует о его не склонности к риску, выбирает ва­риант обращения в правительство за разъяснениями, поскольку ожидаемая полезность альтернативного варианта решения (не обращаться за разъяснениями и действовать наудачу) составляет всего 0,7.

Риск -менеджмент

Не нашли, что искали? Воспользуйтесь поиском по сайту: