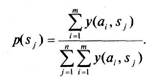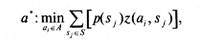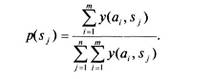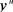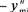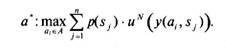Иллюстрация недостатка критерия Вальда

Гарантированный результат в табл. 5.4 для стратегии а, равен 0,99, а для альтернативы а₂ он равен 1,0. Следовательно, фор­мально по критерию Вальда наилучшей следует считать альтер­нативу а₂. Но на самом деле каждому понятно, что с точки зре­ния не формального, а практического бизнеса результаты 0,99 и 1,0 - это одно и то же. Поэтому, формально получается, что мы выбираем стратегию, которая для всех связанных с ней ситуаций дает один и тот же результат. А вот для стратегии а/практически такой же результат получается только в одной из связанных с ней ситуаций, а в остальных своих ситуациях эта стратегия на

Риск -менеджмент

три порядка лучше, чем стратегия а₂. И об этой формальной сто­роне критерия Вальда нужно постоянно помнить. Таким обра­зом, этот критерий принимает во внимание только наихудшие значения для конкретной стратегии, а то, какие по величинам наилучшие результаты дает эта же стратегия, а также — сколько таких «лучших» результатов у нее — этот критерий вообще не принимает во внимание.

Критерий Сэвиджа. Это критерий ЛПР, склонного к риску, являющегося крайним пессимистом. В этом критерии использу­ют не результаты критерий Сэвиджа. Это критерий ЛПР, склон­ного к риску, являющегося крайним пессимистом. В этом кри­терии используют не результаты у(а_п s_j),а так называемое «со­жаление» от неиспользованных возможностей. По замыслу автора, величина сожаления вычисляется для каждой возмож­ной ситуации как разность между наилучшим при данном со­стоянии природы результатом и всеми текущими для этого со­стояния. Обозначим «сожаление» в ситуации (о,., я,) через г(а,,5_у)Тогда формальное выражение для величины сожаления в ситуации (д,,^)выглядит следующим образом:

г(а,.,s_f) = maxy(a,, s ) -у(а,,s_f\

^J а,е_Л ■'

то есть из наилучшего результата тах_у(я_;,s_yдля фиксирован­ного состояния Sj природы вычитаем текущий результат у(а,,, s_:) для этого состояния, и эта разность характеризует величину не­довольства, «сожаления» ЛПР своим необдуманным поступком. После того как для всех ситуаций сожаления вычислены, мы мо­жем заменить матрицу \у^ результатов yia^Sj) на матрицу |г_у величин сожалений z(d_ltSj). Получим матрицу сожалений для ситуаций нашего примера. Почему может сожалеть думающий предприниматель? Потому только, что он знал, как нужно по­ступить, но — не поступил (почему-то). Как это соотносится с нашим примером? А вот как. Предположим, предприниматель точно знает, что конъюнктура на рынке товара сложится в точ­ности как в s, состоянии «природы». Как он тогда поступит? Он выберет наилучшую из его стратегий, чтобы получить наиболь­шую прибыль. Формально это означает, что нужно найти в столбце 5, наилучший результат. Применив эти рассуждения к исходным данным нашего примера, мы увидим, что наилучший результат 32 065 руб. дает применение стратегии а_г А если пред-

Глава 5. Анализ рисков неустановленной природы

принимателъ применит для этого же состояния рынка иную стратегию, например, а₂, получит он ту же прибыль? Нет, при­быль составит всего 29 150 руб., то есть он потеряет 2915 руб. и будет сожалеть о своем нерациональном поступке. Следователь­но, если мы вычтем из наилучшего результата в столбце я, все остальные результаты этого же столбца, то мы получим для этого столбца величины z(a_n s _J сожалений в рублях. Нулевое по вели­чине сожаление будет только для ситуации (о,, 5,). Затем так же можно вычислить сожаления и для остальных состояний рынка. Матрица сожалений представлена в табл. 5.5.

Т а б л и ц а 5.5 Результаты расчетов величин сожалений z(a_iy *,.)для торговли и всех состояний рынка аналогичных товаров

Далее Сэвидж предложил для оценки предпочтительности альтернатив проводить анализ так же, как в методе Вальда: >• для каждой альтернативы а. получить оценку гарантиро­ванного, то есть наибольшего сожаления:

z~ (a,): max. zia^Sj);

> найти наилучшую альтернативу а , обеспечивающую ЛПР наименьшее гарантированное сожаление:

a": minmaxz(a,, s_i).

В соответствии с записанным формальным правилом крите­рий Сэвиджа называют также критерием минимаксных сожале­ний. В табл. 5.6 представлены значения гарантированных сожа­лений

Риск-менеджмент

Т а б л и ц а 5.6 Гарантированные сожаления для стратегий

Что же мы видим? Наилучшей по критерию Сэвиджа являет­ся стратегия а_{\ Это противоречит тому, что мы получили, когда использовали критерий Вальда. Не удивляет? - Не должно! Бы­ло бы гораздо больше подозрений, если бы оценки по столь раз­ным критериям в результате совпали. Ведь эти критерии — для разных по своим устремлениям ЛПР: критерий Вальда для того, кто боится много проиграть, а критерий Сэвиджа - мало выиг­рать. Но, в принципе, разумеется, совпадения результатов при­менения разных критериев возможны.

Итак, поскольку теоретической основой обоих рассмотрен­ных нами критериев является принцип наилучшего гарантиро­ванного результата (для критерия Вальда — сам результат, а для критерия Сэвиджа — сожаление), основные достоинства и не­достатки у критерия Сэвиджа те же, что и у критерия Вальда. Но есть у критерия минимаксных сожалений и специфический не­достаток. Дело в вычислении величин сожалений по ситуациям. Поэтому критерий Сэвиджа чувствителен к составу исходного множества альтернатив. Пусть игра с природой моделируется матрицей, представленной в табл. 5.7.

Т а б л и ц а 5.7 Матрица гипотетической игры с природой

При этом пусть 0 < р< а < 1. Тогда сожаления для указанной матрицы результатов будут такими, как это отображено в табл. 5.8.

Глава 5. Анализ рисков неустановленной природы

Т а б л и ц а5

Матрица сожалений гипотетической игры с природой

Наименьшие гарантированные сожаления, равные 1 - а, обеспечивает стратегия я,,которая и является наилучшей для рассматриваемого примера.

А теперь пусть число стратегий увеличили, и матрица рас­сматриваемой нами гипотетической игры (см. табл. 5.7) приоб­рела вид, представленный в табл. 5.9. Достаточно просто убе­диться, что решение в подобной игре неустойчиво к добавлен­ной «посторонней» альтернативе и зависит от того, останется ли она в числе стратегий ЛПР или нет.

Т а б л и ц а 5.9 Матрица игры с природой, неустойчивой по отношению к «посторонней» альтернативе

Таким образом, эта матрица, представленная в табл. 5.9, по­лучена из матрицы предыдущего примера с добавлением еще од­ной строки для стратегии а₃. По матрице результатов с добавлен­ной альтернативой вычислим значения сожалений. Они будут такими, какими они представлены в табл. 5.10.

Таблица 5.10

Матрица сожалений игры с природой, неустойчивой по отношению к «посторонней» альтернативе

Риск -менеджмент

Так что же получается? - Критерий Сэвиджа выделяет в ка­честве наилучшей стратегию а₂, хотя, если по какой-либо причи­не стратегия а₃ не сможет быть реализована, то наилучшей будет альтернатива а,, а а₂ перестанет быть наилучшей. Таким обра­зом, критерий Сэвиджа не обладает свойством независимости (устойчивости) от «посторонних» (дополнительных) альтерна­тив. Это очень важно помнить, если вы решите дополнять пере­чень уже имеющихся альтернатив какими-то новыми.

Критерий Гурвица. Критерий используют для следующих эле­ментов системы предпочтений ЛПР: оно безразлично к риску и является реалистом. В качестве количественной характеристики для каждой стратегии предпринимателю рекомендуется исполь­зовать величину у(а,,у), которая формируется в виде линейной функции наихудшего (пессимистического) и наилучшего (опти­мистического) для нее значений прибыли. Для этого используют специальный коэффициент пессимизма-оптимизма, называе­мый также коэффициентом Гурвица. Обозначим этот коэффи­циент через у. Значения коэффициента выбирают из диапазона [0; 1] по правилу:

>- у = 0, если ЛПР считает, что состояние «природы» в опера­ции будет самым благоприятным (оптимистический про­гноз);

>- у = 1, если ЛПРсчитает, что состояние «природы» в опера­ции будет самым неблагоприятным (пессимистический прогноз);

>- 0 < у < 1, если ЛПР считает, что состояние «природы» в операции будет не самым плохим, но и не самым благо­приятным.

Каждую альтернативу оценивают взвешенным результатом вида:

j(fl,,у) = у • mmy(a_l,s_j)+ (1 - у) • max.Ka,,)..

Затем наилучшую альтернативу а" отыскивают обычным по­рядком, то есть максимизацией величин у(а,, у): a*: max у(а_п у). Легко заметить, что если у = 0, то модель выбора по критерию Гурвица отражает предпочтения ЛПР, руководствующегося пра­вилом «все сложится самым удачным образом» (крайний опти­мист); если у = 1, то сразу получается критерий Вальда, который

Глава 5. Анализ рисков неустановленной природы

моделирует крайне пессимистичное отношение ЛПР к возмож­ным условиям проведения операции.

Значение коэффициента у может быть назначено ЛПР эври­стически из интервала [0; 1] или это значение можно оценить с использованием специальных процедур, сходных с процедурами определения субъективных вероятностей.

Определим наилучшую по критерию Гурвица стратегию для нашего примера. В табл. 5.11 представлены значения линейной функции .Ко,.,у) Гурвица при значении коэффициента пессимиз­ма-оптимизма у, равного 0,2.

Таблиц а 5.1 1 Значения линейной функции у(а_;,у)Гурвица при у = 0,2

Таким образом, по критерию Гурвица наилучшей оказывает­ся стратегия а₄. Понятно, что наилучшим это решение может быть признано только тем предпринимателем, который считает себя нейтрально относящимся к риску в части осознания воз­можности получения как наилучших, так и наихудших результа­тов, то есть реалистом. Кроме того, он считает, что возможности таких альтернативных исходов не одинаковы. Поэтому он при­дает больший вес оптимистичному исходу, а не пессимистично­му. Причем эта его личная уверенность достаточно сильная, и поэтому значение величины у — коэффициента пессимизма-оп­тимизма, называемого также коэффициентом Гурвица, составляет величину 0,2. Если бы предприниматель отдавал таким исходам одинаковый вес - принял бы у = 0,5, - то получилось бы две оптимальной по Гурвицу стратегии, а₂и а₄,а если бы он был бо­лее пессимистично настроен (у = 0,8) — наилучшей оказалась бы стратегия а₃.

Риск-менеджмент

Заметим, что критерий Гурвица может не различать явно различающиеся по предпочтительности стратегии в силу того, что каждой из них ставит в соответствие оценку, являющуюся линейной комбинацией только наихудшего и наилучшего ре­зультата для альтернатив. Поясним это на следующем примере. Пусть игра с природой описывается матрицей, представленной табл. 5.12.

Т а б л и ц а 5.12 Матрица игры с природой, иллюстрирующая недостаток критерия Гурвица

Стратегии а_} и аг отличаются существенно по предпочти­тельности, так у первой альтернативы только один ненулевой исход, а у второй их три (весьма значительные по величине). В то же время у них одинаковые наилучшие (равные 1000) и наи­худшие (равные 0) результаты и, следовательно, по критерию Гурвица эти альтернативы эквивалентны. Но для практики, ра­зумеется, вторая стратегия несомненно лучше первой.

Критерий Лапласа-Бернулли. Это критерий для ЛПР, не склонного к риску и являющегося реалистом. В его основу поло­жена концепция недостаточного основания Лапласа и принцип рандомизации, о котором мы уже говорили. Согласно концеп­ции недостаточного основания, если нет никаких оснований по­лагать, что какие-либо из п возможных состояний природы бо­лее возможны по отношению к другим, то их целесообразно по­лагать субъективно равновозможными, то есть имеющими

одинаковую p(s,) = - субъективную вероятность появления. По-

п

еле этого, опираясь на принцип рандомизации, считаем ситуа­цию случайной и применяем критерий наибольшего среднего ре­зультата. В итоге критерий Лапласа—Бернулли принимает вид:

a max М (а,) = max ^T ^p(s )y(a_n s )\ = max —^(fl,-, s_j).

Глава 5. Анализ рисков неустановленной природы

Результаты расчетов величин средней субъективно ожидае­мой прибыли для стратегий торговли представлены в табл. 5.13.

Т а б л и ц а 5.13 Результаты расчетов величин средней субъективно ожидаемой прибыли для стратегий торговли

Расчеты для исходных данных нашего примера показывают следующее: наилучшей по критерию недостаточного основания Лапласа—Бернулли следует считать стратегию а₂.

Для наглядности и в качестве промежуточного итога сведем результаты применения всех классических критериев в табл. 5.14, где наилучшая стратегия отмечена звездочкой в строке для соот­ветствующей стратегии торговли.

Таблица 5.14

Результаты применения классических критериев

А теперь в дополнение к рассмотренным классическим кри­териям несколько новых критериев принятия решений в услови-287

Риск -менеджмент

ях природной неопределенности. Первый шаг на этом пути — модификация классического критерия путем ослабления его очевидных недостатков.

Модифицированный критерий Гурвица. Основная идея моди­фикации состоит в том, чтобы при оценке каждой альтернативы помимо наименее и наиболее предпочтительных результатов присутствовали бы и промежуточные. В итоге критерий принял вид:

а':таху(а_пу),

q,g.A

при ограничении

где у"""¹"¹ - установленный ЛПР уровень притязаний по средне­му арифметическому из величин возможных результатов для альтернатив.

Предположим, у""""" = 22 000 руб. При таком значении уров­ня притязаний только для первых двух альтернатив выполняется условие превышения средних арифметических значений резуль­тата над уровнем притязаний. Значения средних арифметических результатов составляют 22 591,25 руб. и 23 320 руб. соответствен­но. В этом легко убедиться, рассмотрев данные для результатов применения критерия Лапласа—Бернулли. Среди страте­гий-претендентов наилучшим значением линейной функции Гурвица у(а,,у)= у • mmy(a,.,sf) (1 -у)maxy(a_u)> обладает

вторая стратегия (28 567 руб. у первой стратегии и 29 733 руб. у второй). Таким образом, а = а₂.

Модифицированный критерий Сэвиджа. При модификации введено расширенное толкование понятия «сожаление». Если субъектом движет желание коренным образом изменить ситуа­цию, добиться существенного выигрыша в ней, пусть даже це­ной каких-то потерь, то «риск» — это просто плата за возмож­ность получения наиболее благоприятного исхода в операции, а «сожаление» — мера подобно трактуемого риска. В результате, в дополнение к классическому понятию «сожаления» предложено измерять его также и величиной разности между уровнем притя­заний и текущим результатом. Поэтому вполне возможно, что могут быть получены «сожаления» как со знаком плюс, так и со знаком минус. Иными словами, отрицательное сожаление озна-

Глава 5. Анализ рисков неустановленной природы

чает «значительный успех», выраженный в превышении полу­ченного результата над выбранным уровнем притязаний. А далее все просто: использован тот же подход, что и в модифицирован­ном методе Гурвица — введено понятие «уровень притязаний по сожалениям». Обозначим эту величину через z"'"'"".В итоге та­кой модификации получаем критерий следующего вида:

а *: min max z(a,, s,)

1 "

при ограничении — Удя,, s ■)< z"¹"""'. П ₇=T~

Пусть в рамках рассматриваемого нами примера z""""" — 9000 руб., то есть при сожалениях не превышающих 9000 руб. предприни­матель готов рассматривать кандидаты на звание лучшей страте­ги. Оказывается, что среднее арифметическое значение сожале­ний для стратегий только в одном случае удовлетворяет уровень притязаний по величинам сожалений. Только для стратегии а₂ величина среднего арифметического сожалений составляет 8745 руб., а у трех остальных стратегий эта величина выше поро­гового значения в 9000 руб. Поэтому у предпринимателя нет вы­бора — перед ним дилемма: или он будет руководствоваться стратегией а₂, или ему предстоит расширить множество альтер­натив и при этом постоянно помнить, к чему может привести добавление «посторонних» альтернатив.

Разумеется, это не все модификации классических методов, а лишь часть их силы.

Однако имеются новые критерии, позволяющие напрямую оперировать предложенными формальными характеристиками личности Л ПР.

Критерий субъективно средних результатов соответствует предпочтениям ЛПР, не склонного к риску, являющегося разумным оптимистом. Такое ЛПР оценивает состояния природы величина­ми результатов, но рассматривает результаты через призму субъек­тивного восприятия состояний природы. Субъективные вероятно­сти состояний природы принимаются пропорциональными сум­марным результатам для каждого состояния «природы». Согласно этому критерию лучшей следует считать ту стратегию, которая приводит к максимальному субъективно среднему результату:

Риск-менеджмент причем субъективные вероятностиp(Sj) определяются по формуле

При тех исходных данных, которыми мы оперируем в общем для анализа примере, значения субъективных вероятностейp(Sj) конъюнктуры рынка составят:

p(s,) = 0,28; p(s₂) = 0,36; p(s₃) = 0,23 иp(s₄) = 0,14.

Окончательно величины субъективно средних результатов для стратегий получаются равными тем, которые представлены в табл. 5.15.

Таблица 5.15

Величины субъективно средних результатов для стратегий

Таким образом, по критерию субъективно средних результа­тов наилучшей является стратегия а_ь дающая в среднем при­быль в 26 412,43 руб.

Предположим теперь, что ЛПР склонно к риску и является ра­зумным оптимистом. В таком случае оно, скорее всего, оценивает ситуации величинами сожалений и намерено измерять субъек­тивные вероятности возможных состояний «природы». Величины субъективных вероятностей состояний природы вычисляем про­порционально суммарным результатам для каждого состояния. А сам критерий — его можно назвать критерием средних субъек­тивных сожалений — выглядит так:

причем величины Р(Sj,) субъективных вероятностей определяют по формуле:

Глава 5. Анализ рисков неустановленной природы

В нашем примере величины субъективных вероятностей для этого критерия те же, что и для предыдущего критерия. Умно­жив их на соответствующие ситуациям величины сожалений z{a,,, Sj), получаем величины средних субъективных сожалений такие, как это представлено в табл. 5.16.

Таблица 5.16

Величины средних субъективных сожалений

7807,13

Л2

9708,217

аз

16 678,87

Л4

10 494

Минимальное сожаление соответствует применению страте­гии Я].

Критерий субъективной вероятностной гарантии. Этот крите­рий характерен для ЛПР безразличного к риску, который может указать субъективные оценкиp(Sj)вероятностей состояний при­роды в числовой форме, а также требуемый уровень результата (уровень притязаний). Критерий рекомендует считать лучшей ту стратегию, которая приводит к наибольшему значению вероят­ности получения результата не хуже требуемого:

—те состояния природы, для стратегии й_/ оказался лучше

Предположим, анализируя с помощью экспертов возможные уровни конъюнктуры рынка аналогичных товаров, предпринима­тель оценил попарно возможные состояния рынка и применил процедуру определения субъективных вероятностей через вербаль­ные высказывания типа «более вероятно», «равновероятно», «менее вероятно». Результаты оценки составили следующие величины:

/>(S|) = 0,38; p(s₂) = 0,36; />(s₃) = 0,20 и/»(s₄) = 0,06.

Риск-менеджмент

Уровень притязаний y'""""^J по результатам установлен в 30 000 руб. Используя значения прибыли для ситуаций, найдем те ситуации, для которых результаты превышают 30 000 руб. (табл. 5.17).

Таблица 5.17

Ситуации (а,,s.), значения величин прибылиj»(a,,Sj) для которых превышаюту""""' = 30 000 руб.

Анализ данных табл. 5.17 показывает следующее. Для первой стратегии а₇ вероятность получения результата, превышающего установленный уровень у^пР^ит« = 30000 руб., составляет p(sj) +p(s2) = 0,38 + 0,36 = 0,74; для стратегии а₂ — вероятность этого события равна p(s^ — 0,20, для стратегии а₃ вероятность превышения уровня притязаний равна нулю, а для стратегии a₄—p(s₂) = 0,36. В итоге по критерию субъективной вероятност­ной гарантии наилучшей следует признать стратегию Э|.

Критерий субъективно ожидаемой полезности моделирует вы-бор ЛПР, которое не только может указать субъективные вероят­ности состояний природы в числовой форме, но и указать свою индивидуальную функцию полезности для рассматриваемых ус­ловий. Эмпирическая функция u^N(y) для оценки полезности ре­зультатов у в условиях «природного» риска имеет вид степенной зависимости

u^N(y)=y\

где у — нормированные результаты операции; а - параметр функции.

Эта функция трансформирует значения нормированных ре­зультатов операции в отрезок [0; 1]. Нормирование результатов проводят по линейной зависимости вида:

Глава 5. Анализ рисков неустановленной природы

у

У - V .

v max л mm

где у"— результат в натуральной шкале;

y"_mi =minmmy(, s ) — минимальный из результатов для всех

ситуаций⁴ в натуральной шкале;

j max = max max ^(а₍, 5 ) — максимальный из всех результатов в

натурал^аьной шкале.

Параметру а функции устанавливают значения из следую­щей шкалы:

0,125 -если существенна несклонность к риску; 0,5 - если незначительна несклонность к риску; а = { 1,0 - если взвешенное отношение к риску; 2,0 - если незначительна склонность к риску; 5,0 - если существенна склонность к риску.

В итоге наилучшей следует считать ту стратегию а*, которая характеризуется наибольшей ожидаемой субъективной полезно­стью результатов:

Применим этот критерий для сравнения стратегий, предпо­лагая, что а = 5. Предварительно вычислим нормированные зна­чения величин прибыли. Они представлены в табл. 5.18.

Таблица 5.18 Нормированные значения величин прибыли

Риск-менеджмент

Значения величин функции и"(у) = у "полезности предпри­нимателя сведены в табл. 5.19.

Таблица 5.19

Значения величин функции и^Л (у )= у" полезности предпринимателя

Теперь остается вычислить ожидаемую субъективную полез­ность. Результаты вычислений сведены в табл. 5.20.

Таблица 5.20

Не нашли, что искали? Воспользуйтесь поиском по сайту: