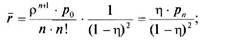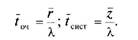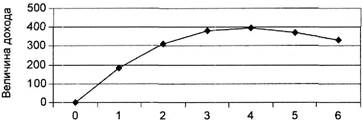
Результаты расчета доходности функционирования юридической консультации

Глава 3. Управление стохастическими рисками

Продолжение табл. 3.7

На основании данных, представленных в табл. 3.7 и отобра­женных в виде графика на рис. 3.10, следует, что оптимальным по максимуму получаемого юридической консультацией дохода при тех же параметрах служебного помещения следует считать увеличение штата юристов до четырех человек. При таком соста­ве специалистов-консультантов доход этой организации соста­вит более 395 руб./час против 313,73 руб./час, которые юридиче­ская консультация получает в положении status quo, когда в ней трудятся только два консультанта.

Торговля садово-огородным инвентарем, инструментами и строительными материалами. Торговля подобными товарами в крупных центрах самообслуживания является не только про­грессивной, но и удобной формой обслуживания покупателей. Она также хороша и тем, что позволяет легко организовать авто­матизированную систему сбора данных об интенсивностях пото­ков посетителей, о доле тех из них, кто по разным причинам ушел без покупки, и т.п. Этому способствует наличие у подоб-

Риск-менеджмент

ных торговых центров систем автоматизированного допуска по­сетителей к местам расположения товара и автоматизированного учета и списания купленного товара после его оплаты в кассе.

Большую часть товара в центрах торговли садово-огородным инвентарем, инструментами и строительными материалами по­сетители отбирают сами, непосредственно подержав размещен­ный на стеллажах и подиумах товар в руках. Однако некоторая часть товара, представляющего сложную технику или дорогой инструмент, покупатель, как правило, выбирает после консуль­таций с менеджером в торговом зале. Время консультации при этом оказывается случайным, но распределение этого времени, как правило, — показательное. Поток посетителей, обращаю­щихся к менеджеру за консультацией, также случаен. Поэтому менеджер может то стоять без дела (к нему никто не обращается за разъяснениями), то к нему может выстроиться очередь за кон­сультацией. Но ведь не каждый из потенциальных покупателей сложной техники или дорогого инструмента готов долго ожидать своей очереди и задать менеджеру вопрос.

Некоторые, особенно нетерпеливые клиенты, могут просто уйти без покупки. Поэтому для снижения риска ухода посетите­ля без покупки из-за того, что этот нетерпеливый клиент не же­лает или не в состоянии ждать, пока менеджер освободится, таких консультантов должно быть возле места расположения указанного товара несколько. Но сколько? Разумеется, опти­мальное число консультантов зависит и от интенсивности пото­ка покупателей, и от доли тех, кто заинтересован в покупке именно дорогой или сложной техники и инструмента, и от вели­чины среднего времени консультации, и от ряда других, менее значимых факторов.

Предположим, что после консультации с менеджером в зале посетитель выбрал интересующий его инструмент и, отстояв очередь в кассе, оплатил товар. Закончились ли на этом его взаи­моотношения с торговым центром? Нет, не закончились. Есть еще одна специфическая особенность заключения сделки куп­ли-продажи подобных товаров, а именно: обязательная провер­ка работоспособности изделия и оформление гарантийных обя­зательств на купленный товар. В итоге операция по покупке сложной садово-огородной техники, инструмента или инвента­ря превращается в трехстадийный процесс: выбор товара, его

Глава 3. Управление стохастическими рисками

оплата в кассе, проверка работоспособности и оформление га­рантийного талона на приобретенный товар.

Для оценки экономической выгоды процесса работы торго­вого центра его руководству крайне необходима информация об эффективности процессов на каждой из стадий. Такую инфор­мацию можно получить, если будут известны следующие харак­теристики процессов обслуживания в торговом центре покупа­телей сложной техники (инструмента):

A, Q, Р_оп — абсолютная и относительная пропускные спо­собности и вероятность отказа в обслуживании соответственно;

г,, г₂, г_ъ — среднее число клиентов в очереди на первой, вто­рой и третьей стадиях обслуживания соответственно;

Z\, Z-i, z₃ —среднее число клиентов, связанных с первой, второй и третьей стадиями обслуживания соответственно;

*11 ■> ¹т^}> Сч* —среднее время ожидания клиента в очереди на первой, второй и третьей стадиях обслуживания соответственно;

*Шт> ILL* ^{а1т —среднее время пребывания покупателя в первой, второй и третьей стадиях процесса обслуживания соот­ветственно;

г — общее среднее число покупателей во всех очередях;

z - общее среднее число покупателей сложной техники (ин­струмента), совершающих покупку в магазине;

t₀₄ — общее среднее время, проводимое покупателем слож­ной техники во всех очередях;

t_сжт — общее среднее время, затрачиваемое покупателем на приобретение сложной техники в торговом центре.

Адекватным модельным аналогом рассматриваемого нами процесса торговли может служить модель функционирования многофазной СМО с очередью. В подобной системе входящий поток каждой последующей фазы является выходным потоком предыдущей и в общем случае имеет последействие. Однако, ес­ли на вход СМО с неограниченной очередью поступает простей­ший поток заявок, а время обслуживания показательное, то выходной поток этой СМО - простейший с той же интенсивно­стью, что и входящий. Поэтому многофазовую СМО с неограни­ченной очередью перед каждой очередной фазой, с простейшим входящим потоком заявок и показательным временем обслужи­вания на каждой фазе можно анализировать как простую после­довательность простейших СМО. Если же очередь к какой-либо фазе ограничена, то выходной поток в этой фазе перестает быть

Риск-менеджмент

простейшим и вышеуказанный прием можно применять только в качестве приближенного.

Учитывая эти замечания, применим для анализа экономиче­ской эффективности работы рассматриваемого нами торгового центра математический аппарат, описывающий работу простей­шей многофазной СМО с очередью. Будем рассматривать три последовательные стадии процесса работы с покупателем торго­вого центра как три отдельные СМО со своими характеристика­ми. Исходные данные для моделирования и оценки эффектив­ности многостадийного процесса работы с покупателями слож­ной техники в торговом центре представлены в табл. 3.8.

Та бл и ца 3.8 Исходные данные для моделирования многостадийного процесса работы с покупателями торгового центра

Глава 3. Управление стохастическими рисками

На первой стадии процесса происходят консультации поку­пателей с менеджером в зале и выбор товара. Поток посетителей простейший с интенсивностью 30 чел/час. У стендов с интере­сующим нас товаром работают два менеджера-консультанта. Среднее время обслуживания на этой стадии 6 мин. Не каждый из потенциальных покупателей сложной техники или инстру­мента готов долго ожидать своей очереди задать менеджеру во­прос. В итоге часть клиентов торгового центра, не дождавшись возможности задать свои вопросы менеджеру, отказываются от покупки именно этой техники и переходят к самостоятельному выбору иных товаров в торговом центре. Следовательно, подоб­ных клиентов торгового центра можно моделировать «нетерпе­ливыми» заявками, покидающими СМО через случайное время ожидания, подчиненное показательному закону распределения. Среднее время «терпеливого» ожидания в очереди для подобных клиентов в табл. 13.8 определено в 15 мин.

Таким образом, все случайные времена событий на первой стадии процесса имеют показательный закон распределения. В итоге процесс обслуживания клиентов торгового центра на стадии консультации и выбора товара можно смоделировать по­средством процесса функционирования простейшей двухка-нальной СМО «нетерпеливыми» заявками и неограниченной очередью. Учтем, что интенсивность входного потока заявок в общем случае уменьшается из-за того, что некоторая доля по­тенциальных покупателей вообще ничего себе не подберет и уй­дет из торгового центра без покупки. Доля а посетителей, кото­рые не выбрали товар, определена в 15%.

Основные соотношения для моделирования простейшей многоканальной СМО «нетерпеливыми» заявками и неограни­ченной очередью являются:

>- финальные вероятности состояний СМО

где р

—, Р = v —

и V

интенсивность потока уходов, приходя-

щаяся на одну заявку, стоящую в очереди; указанные финальные вероятности всегда существуют, если только р > 0;

>- суммарная средняя интенсивность потока уходов, прихо­дящаяся на все заявки, стоящие в очереди, равна vr; зна­чит, интенсивность входного потока заявок уменьшается на эту величину, и абсолютная пропускная способность СМО А и составляет: А =^-уг;именно такая величина будет определять величину интенсивности потока заявок для последующих стадий процесса; эту же характеристику можно определить из соотношения интенсивности обслу­живания и среднего числа занятых каналов: А = к • ц; >- с учетом того, что не все посетители, а только их доля (1-а) найдет себе товар для покупки, абсолютная пропускная способность СМО будет равна величине А = (1 - а)Х - vr; именно такими, то есть по итогам работы первой стадии процесса, будут интенсивности входных потоков заявок для второй и третьей стадий;

>• относительная пропускная способность составит Q = —;

л,

>■ среднее число к занятых каналов следует подчитать на­прямую как математическое ожидание случайной вели­чины числа занятых каналов с возможными значениями 0, 1,2, ..., п и соответствующими вероятностямиPo-.pi.p2, ' ••■> Pn-h 1'~(/'<Я"7>]~*~р• • •+ Pn-l)\\ это выражение имеет вид:

к = lpi+2p₂+..+ (п - \)р_п-1+п[\ ~(Po⁺Pi+P2+ •••+ P„-i)Y,

>- среднее число заявок в СМО z — г + к;

>- средние времена пребывания заявки в очереди и в системе равны, как обычно, величинам t_№, =r / Хи /_сист = z I'k со­ответственно.

На второй стадии покупатели, выбравшие товар, должны оп­латить покупку. Пунктов расчета, как правило, в подобных тор­говых центрах несколько. Однако необходимо учитывать специ­фику их расположения и особенности продаваемого товара. Де­ло в том, что обычно подходы к пунктам расчета за покупку разграничены турникетами. Товар, представляющий собой садо­во-огородный инвентарь, оборудование дачных участков, строи­тельные материалы и т.п., достаточно громоздкий, и покупатели перемещаются по торговым залам, транспортируя его на доста­точно крупных тележках. С такой тележкой в узком проходе ме­жду турникетами особенно не развернешься.

Все это приводит к тому, что даже при нескольких пунктах расчета за покупку покупатель должен стоять в одну очередь, а именно в ту, в какую он попал по собственной воле или по воле случая. Выбраться из такой очереди и перейти в другую - весьма проблематично, учитывая психологический настрой сзади стоя­щих покупателей, также перегруженных покупками. В результа­те работу расчетного пункта и весь процесс на второй стадии приобретения товара в торговом центре приходится моделиро­вать как работу одноканальной СМО с неограниченной очере­дью и средним временем расчета с покупателем, равным 5 мин.

Основные математические соотношения для моделирования простейшей одноканальной СМО с неограниченной очередью являются:

> р₀=1 -р;р_к=р^к(1-р), для к=1, 2, 3, ...; причем финаль­ные вероятности существуют только для случая, когда

^Х 1;

характеристики эффективности определяются выражениями вида:

A=KQ=lf_m = bk=_P;r=₁^-;z=T*-;i_aKt =f;/„=-

1-р 1-р X X

Риск-менеджмент

Третья, последняя стадия процесса, — это контроль и оформление гарантии на приобретенный товар. Входной поток имеет такую же интенсивность, как и для второй стадии. На контроле работают четыре специалиста. Среднее время обслу­живания на этой стадии 3 мин. Адекватной моделью процесса контроля качества и оформление гарантии на приобретенный товар является многоканальная СМО с неограниченной очере­дью. Работа подобной СМО описывается следующими характе­ристиками:

>- финальные вероятности

(, р р² р^л р"^+| 1 ''

1! 2! п\ п п\ 1 -т|

Рк =тт</>₀;...ДДЯ ' Z^k*ⁿ'>P>»r ^=J7------- ;■/»„;... для г>1; они

к: п -я!

существуют только для случая, когда г\ - — - — < I; А - А^ 0 = 1;

Р_0ТК =0;

>- средняя длина очереди

>- среднее число занятых каналов (или вероятность того, что канал занят) к = — = р;

>- среднее число заявок в системе z =r+ к =г+ р >- средние временные характеристики процесса:

На основании представленных в тексте и табл. 3.8 исходных данных по всем приведенным нами формулам были проведены модельные расчеты, результаты которых сведены в табл. 3.9.

Глава 3. Управление стохастическими рисками

Т а б л и ца 3.9 Результаты модельных расчетов для трех стадий процесса обслуживания посетителей торгового центра

Из полученных результатов моделирования следует, что средние времена пребывания покупателя сложной техники и ин­струмента в очередях и в торговом центре составляют величины ^/<«^=/^^)+/,«"^f ^^>й:20, 2 м и н и/,_жт = ^^+/™™ ⁺ ^1⁾т^;39мин со­ответственно. Анализ относительных величин для этих данных позволяет сделать вывод о том, что около 43% общего времени пребывания в магазине занимают контроль и оформление гаран­тии на приобретенный товар. При этом имеющееся количество специалистов на этой стадии процесса (четыре специалиста) можно считать избыточным, поскольку в среднем заняты только 2,8 чел. А вот в очереди на контроль пребывает в среднем всего 1,1 чел. В то же время на первой стадии консультации и выбора товара в очереди на консультацию стоят в среднем 2,8 чел, и, учитывая, что среди посетителей торгового центра есть «нетер­пеливые», то для улучшения обслуживания покупателей целесо­образно одного специалиста из отдела контроля снять и поста­вить его консультантом в торговом зале. Следовательно, таким простым структурным изменением можно, во-первых, умень­шить время ожидания клиентом консультации, а, во-вторых, снизить вероятность того, что «нетерпеливые» клиенты уйдут, не приобретя дорогого товара. Для получения более точной, коли­чественной оценки выгодности подобных структурных измене­ний потребуется провести все расчеты по изложенной методике при новых исходных данных.

Риск-менеджмент

Выпуск лотерейных билетов. Лотерейный бизнес широко рас­пространен во всем мире. Основу процветания всевозможных лотерей составляют устойчивое желание весьма большого числа людей мгновенно обогатиться. Учитывая случайность механизма разыгрывания лотереи, а также массовый характер участия в ней игроков, для оценки рисков и обоснования показателей затрат и доходности в лотерейном бизнесе широко применяют вероятно­стные модели.

Предположим, что устроители лотереи для привлечения мак­симального числа участников гарантируют, что «в каждом лоте­рейном билете — автомобиль!» Лотерейный билет оформлен в виде карточки, на которой размещена таблица 4 на 5 (матрица), клетки которой закрыты фольгой. В клетки матрицы внесены какие-то буквы, но среди них обязательно есть десять букв, из которых можно составить слово «автомобиль».

Если игроку удается из двадцати имеющихся клеток открыть ровно 10 клеток (стереть с них фольгу) и в них окажутся буквы, составляющие слово «АВТОМОБИЛЬ», то такой участник лоте­реи получает приз — автомобиль. Одна из возможных случайных комбинаций букв в ячейках матрицы представлена в табл. 3.10.

Таблица 3.10

Не нашли, что искали? Воспользуйтесь поиском по сайту: