
|
|
Тепловая теорема Нернста. Третий закон термодинамикиПри изложении химической термодинамики мы постоянно старались проводить мысль о том, что этот раздел науки не является чем-то застывшим. Напротив, он постоянно развивается во времени. В качестве одного из доказательств этого указывалось на создание теории неравновесной термодинамики, за что И.Р. Пригожин, бельгийский ученый с русскими корнями получил в 1947 г. нобелевскую премию – высшую награду мирового сообщества ученых. Пригожин Илья Романович (родился 25 января 1917 в Москве). Бельгийский химик и физико-химик, с 1953 г. член Королевской бельгийской академии наук, литературы и изящных искусств. В 1969 г. становится ее президентом. Илья Романович окончил Брюссельский университет, с 1962 г. директор Международного института физики и химии в Сольве, с 1967 г. директор научно-исследовательского центра по статистической механике и термодинамике в Техасском университете, г. Остин, США. Работы И.Р. Пригожина посвящены термодинамике и статистической механике необратимых процессов. Развил представления об устойчивости состояний систем, далеких от равновесия. Заложил основы теории, согласно которой наряду с равновесными структурами в природе имеют место диссипативные структуры, возникающие в системах, далеких от равновесия и существующих благодаря обмену энергией и веществом с окружающей средой. Иностранный член АН СССР.
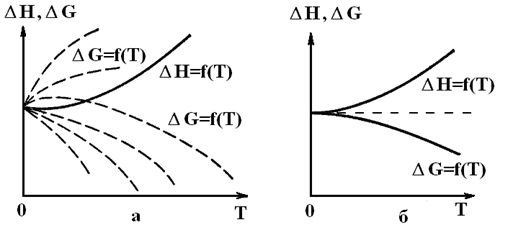
Другим более ранним доказательством того, что термодинамика как некий живой организм, постоянно развивается, явились работы В. Нернста и Дело в том, что ранее указывалось на возможность расчетов DS различных процессов, но ничего не говорилось о расчетах абсолютной величины энтропии вещества, чего невозможно сделать на базе двух рассмотренных выше начал термодинамики. Кроме того, химиков всего мира постоянно интересовала возможность разработки расчетных методов оценки возможности самопроизвольного течения химических реакций без знания, точнее без экспериментального определения термодинамических величин веществ при конкретных условиях, например, при принятых за стандартные. В XIX в Бертло постулировал, что реально могут протекать только экзотермические реакции. Тем самым этот постулат вообще отрицал возможность протекания эндотермических реакций, идущих с поглощением теплоты. А, между тем, экспериментально показано, что таких процессов великое множество. Теперь читатели книги знают, что критерием самопроизвольного течения процесса является характер изменения энтропии, либо свободных энергий Гельмгольца или Гиббса, но никак не знак DН. Однако, с другой стороны, напомним читателю ранее приведенное уравнение DG = DH – TDS, из которого естественным образом вытекает зависимость DH = DG + TDS. А теперь представим себе, что при некоторых условиях величина произведения TDS стала равной нулю или точнее очень близка к нему. Это возможно при очень низких температурах, если, конечно, с понижением температуры адекватно не возрастает изменение энтропии (А то вообще можно прийти к некоторым условиям, когда TDS = const). Если же произведение TDS мало, то DH » DG и DH действительно становится критерием самопроизвольного течения процесса. Естественно, с учетом сказанного встал вопрос об изучении характера изменения теплоемкости с температурой, так как от величины Ср зависит вычисляемое значение DS. Оказалось, что со снижением температуры уменьшаются величины Ср и соответственно DS. Можно было предположить, что при Т = 0 К произведение TDS также равно нулю. Тогда становится абсолютно справедливым и принцип Бертло. Если это так, то зависимости DH = f(T) и DG = f(T) должны иметь одну общую точку при Т = 0. Но если ход кривой, характеризующей DH = f(T), можно получить экспериментально, то для зависимости DG = f(T) имеет место неопределенность, графически выражаемая в виде множества пунктирных кривых (рис. 23).
Рис. 23. Возможные виды зависимостей DH = f(T) и DG = f(T); а – без использования тепловой теоремы Нернста, б – с ее использованием.
Решить задачу уточнения хода зависимости DG = f(T) первое и второе начала термодинамики не позволяют. Тогда Вальтер Нернст постулировал, что зависимости DH = f(T) и DG = f(T) имеют не только общую точку (рис. 23 а), но и общую касательную (рис. 23 б). Иначе говоря,
Из равенства (51) вытекает, что:
иначе говоря, касательная с нулевым тангенсом угла наклона параллельна оси абсцисс (рис. 23б). Это обусловлено следующим. Согласно уравнению Гиббса-Гельмгольца,
Но, если при Т = 0 К, DG = DH, то имеем
Раскрывая эту неопределенность по правилу Лопиталя, получим
Следовательно, справедлив случай, показанный на рис. 17. А теперь, вспомним, что, согласно закону Кирхгофа,
где DСр – разность интегральных теплоемкостей продуктов реакции и исходных веществ. Тогда
Далее было показано и принято, что нулю равны при Т = 0 и сами теплоемкости веществ, то есть
Но
Отсюда следует, что при любом химическом процессе и Т = 0 энтропия остается постоянной. Этот постулат получил название Тепловой теоремы Нернста. Ее математическая формулировка выражается уравнениями (52) и (53). В 1912 г. М. Планк уточнил этот постулат, что тем самым позволило, с учетом 1-го и 2-го начал термодинамики, рассчитать абсолютное значение энтропии и решить проблему химического равновесия, о котором речь пойдет дальше. Формулируется постулат М. Планка следующим образом. Энтропия любого индивидуального вещества в состоянии идеального кристалла при абсолютном нуле равна нулю. S0 =0. Теперь DS = S2 – S1 и при S1 = 0, S = S2. Таким образом, появилась точка отсчета, от которой легко рассчитать величину S, тем более, что она вообще равна 0. При этом нет нужды в оговорке «идеальный кристалл», так как при Т = 0 устойчиво только это состояние. Такой подход является частичным подтверждением правильности уравнения Больцмана, связывающее величину S с числом микросостояний системы S0 =kln1; S0 =0, хотя как указывалось выше, есть и несоответствия. Теперь величина абсолютной энтропии любого вещества может быть вычислена при произвольно выбранной температуре Т. С этой целью следует начать отсчет от Т = 0 и в уравнении (54) взять первый его интеграл в пределах
где Т – температура, начиная с которой известна Ср вещества. Этот интеграл рассчитывают графическим интегрированием (нахождением площади под кривой) экстраполированной к Т = 0 экспериментальной кривой. Следующий интеграл берут в пределах:
если температура плавления рассматриваемого вещества больше 298 К, или
если Тпл < 298 К. Некоторые аспекты, связанные с достижением химического равновесия Ранее было показано, что критерием возможности протекания в системе химического превращения является наличие неравенства
а критерием достижения равновесия наличие равенства
Напомним, что mi – химический потенциал i-го компонента, а dni – изменение его числа молей. Пусть протекает химическая реакция nAA + nBB = nCC + nDD. (55) (В этом случае изменения числа молей компонентов взаимозависимы. Зависимости обычно легко получить из пропорции) Изменение числа моль компонента А ® dnA связано с изменением числа моль второго компонента В, равного dnB dnA связано с dnB nA связано с nB. Отсюда по правилу пропорции
и
Учтем, что в случае прямой реакции, идущей слева направо, изменение числа моль веществ отрицательно, так как количества вещества компонентов уменьшаются. Поэтому перед правой частью уравнений (56) и (57) следует поставить знак минус и они примут вид
Тогда в случае продукта реакции, например, вещества С знак перед правой частью будет положительным, ибо его количество увеличивается
В случае достижения химического равновесия
Следовательно, при достижении равновесия
Здесь нижний индекс i относится к продуктам реакции. Кстати, с таким же успехом можно показать, что в случае равновесия
Из уравнения (60) следует, что для выяснения условий химического равновесия необходимо вычислить Вернемся к уравнению реакции (55) и примем, что все участники ее – идеальные газы, для которых m = m где m
Откуда
Если T = const, то Используем равенство
где Кр – константа равновесия. Примем, в нашем частном случае реакции (55), что nА и nВ – отрицательны (убывают числа моль веществ А и В в процессе реакции), а nC и nD – положительны. Тогда для нее можно записать
Вместо парциальных давлений компонентов можно использовать их концентрации. Но следует учесть, что для смеси идеальных газов справедливо равенство
Подставив уравнение (62) в (63), получим
Иначе говоря, KC(T) = (RT)SnKp(T), где Sn = Snкон – Snнач. Рассмотрим иной случай, когда все компоненты реакции – газы, но они не обладают свойствами идеальных газов. Химический потенциал кажджого такого компонента равен: mi = m где gi – коэффициент фугитивности, а fi – фугитивность i-го компонента газовой смеси. В этом случае выражение для Кр(Т) принимает вид:
Иной случай связан с наличием многофазной системы, в которой одни компоненты – газы, другие – находятся в конденсированном состоянии (жидком или твердом), а сама реакция является гетерогенной. Тогда для первых mконд = m0(T) + RTlnps = m0(T) + RTln(fs), где ps и fs – давление или фугитивность насыщенного пара, которые постоянны при T = const. Уравнение (61) в этом случае приобретает вид:
В этом случае
Применительно к реакции (55) имеем:
но учитываются только pi газов, для конденсированных продуктов они включены в константу равновесия. Если протекает взаимодействие между веществами, находящимися в жидкой гомогенной фазе, то выражение для константы равновесия имеет вид
где ai – активности компонентов, равные произведению их концентраций на коэффициенты активности. И, наконец, выразим Кр(Т) через мольные доли компонентов, которые принимают участие в химической реакции. Мольная доля i-го компонента, находящегося в индифферентном растворителе, равно
где ni – число моль i-го компонента, n0 – число моль растворителя. Если раствор достаточно разбавлен, когда n0 >>
С другой стороны, ni =kpi и nS =kpS. Тогда
Тогда, подставляя уравнение (64) в (62), для реакции (55) получим

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 . (51)
. (51) ,
,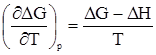 .
. .
. .
. ,
, .
. . (52)
. (52) , что было показано нами ранее. Тогда
, что было показано нами ранее. Тогда . (53)
. (53) , (54)
, (54) ,
, ,
, ,
, .
. (56)
(56) . (57)
. (57) , (58)
, (58) . (59)
. (59) .
. ,
,  .
.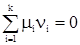 .
. . (60)
. (60) и приравнять нулю.
и приравнять нулю. (Т) + RTlnpi,
(Т) + RTlnpi,

 +
+  0
0 . (61)
. (61) .
. ,
, . (62)
. (62) . (63)
. (63)
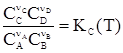 .
. .
. .
. ,
, .
. ,
,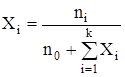 ,
, , то
, то .
.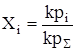 и pi = Хip
и pi = Хip  . (64)
. (64)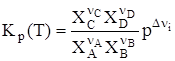 .
.