
|
|
Статистическая интерпретация энтропииВ отличие от необратимых макроскопических процессов, законы классической и квантовой механики симметричны во времени. Иначе говоря, система может идти не только из состояния А в В, но и назад из В в А (равновесия всегда подвижны). Например, потоки молекул идут как в одну, так и в другую сторону. Следовательно, и прямой, и обратный потоки вполне вероятно, исходя из законов механики. Все необратимые процессы – есть следствие движения частиц, подчиняющегося законам механики. Чтобы как-то примирить эти два подхода – термодинамический и механический Л. Больцман высказал предположение, что имеется связь между энтропией и числом микросостояний системы. Более того, чем больше возможное число микросостояний, тем с большей вероятностью система подчиняется законам статистической физики. А необратимые процессы, идущие в сторону возрастания энтропии, определяют направление достижения наиболее вероятного состояния. Равновесные процессы наиболее вероятны, так как в них энтропия достигает максимума. Венцом такого подхода явилось уравнение, носящее имя великого Людвига Больцмана, имеющее вид: S = klnW, (32) где k – константа Больцмана, равная 1,38 × 10-23 Дж/К. Из нее, кстати, легко получить величину универсальной газовой постоянной, равной R = kNA, где NA, в свою очередь, число Амадео Авогадро, равное 6,0226 × 1023, W – число микросостояний системы. Пусть, например, имеется два ящика, в которых могут размещаться частицы. Если в одном ящике их N1, а во втором – N2, то суммарное число микросостояний с перестановкой частиц в ящиках составит
Вместе с тем, как отмечают И. Пригожин и Д. Кондепуди, «в динамике начальные условия всегда произвольны и введении вероятностных функций обычно основано на некотором приближении». Это, конечно, весьма мягко сказано. Так, например, Петер Булер в своей книге «Физико-химическая термодинамика вещества». Санкт-Петербург. «Янус». 2001. 192 с. отмечает, что «Макс Планк, впервые получил уравнение (32). Но сама эта зависимость, носящая название «Уравнение Больцмана», никогда не использовалось для оценки энтропии какого-либо газа или конденсированного вещества». Он объяснил это тем, что величину W нельзя экспериментально определить. Начиная с 1865 г для определения энтропии любого вещества, используют аналитические выражения, вытекающие из второго начала термодинамики, а не зависимость (32). Дело еще и в том, что уравнение (32) приводит к иному, нежели 2-е начало термодинамики, выражению для энтропии. Дело в том, что изменение энтропии связано только с изменением энергии. В то же время в термодинамике предлагается способ расчета изменения энтропии смешения при образовании идеального (в том числе и газового) раствора в виде DсмесиSид, то есть без изменения энергии DсмесиSид = R(XAlnXA + XBlnXB), (33) где, по мнению Булера, XA и XB – задаваемые концентрации раствора. Но, как он замечает, в (33) нет экспериментально определяемой величины, необходимой для сопоставления расчетных и опытных величин. Так как энергия при образовании идеальной системы не изменяется, то использование второго начала термодинамики дает dDсмесиUид = ТdDсмесиSид = 0. (34) Следовательно, из уравнения (31) следует DSсмесиSид = 0, а не уравнение (33). Таким образом, создаваемая последние два века термодинамика - отнюдь не застывшая наука – абсолютная истина. Она живет своей бурной жизнью, интенсивно развивается и уточняется. Химический потенциал и химическое сродство Химиков постоянно интересовал вопрос – какова природа движущей силы химических превращений?. Почему протекают химические реакции? Почему они прекращаются? Часто с этой целью использовалось понятие «Химическое сродство», которое, однако, не было точно определено. Современная термодинамическая формулировка химического сродства возникла, по Один из создателей равновесной термодинамики Джозайей Уиллард Гиббс (11.11.1839 – 28.04.1903). Он разработал теорию термодинамических потенциалов. Изучил условия равновесия гетерогенных систем и сформулировал правило фаз, согласно которому в равновесной гетерогенной системе число фаз не может превышать число компонентов системы, увеличенное на два. Предложил графическое изображение состояния трехкомпонентных систем (треугольник Гиббса). Заложил основы термодинамики поверхностных явлений и электрохимических процессов.
Де Донде не только дал точное определение химического сродства, но и вывел на его основе соотношение между скоростями изменения энтропии и химической реакции. «Все химические реакции вынуждают систему двигаться к состоянию равновесия, в котором суммарное сродство обращается в нуль». Химический потенциал Пусть гетерогенная система состоит из нескольких гомогенных частей, которые могут обмениваться массами вещества (так вначале представил ситуацию Д. Гиббс). Тогда, по его мнению, dU = TdS – pdV + m1dm1 + m2dm2 + … + mjdmj. Коэффициенты m1 … mj он назвал химическими потенциалами. Конечно, он ограничился обменом между частями системы в равновесном состоянии, когда dQ = TdS. Для рассмотрения химических процессов удобнее использовать изменение числа молей. Тогда dU = TdS – pdV + m1dn1 + m2dn2 + … + mjdnj или dU = TdS – pdV + Из уравнения (35) легко получить зависимость энергии как функции S, V и nj. В самом деле
Учитывая понятия deS и diS, целесообразно подобным образом разделить и dnj, имея в виду, что dnj = denj + dinj, где denj – изменение числа молей, вызванное обменом системы с окружающей средой, а dinj – изменение, обусловленное протеканием необратимых химических реакций внутри самой системы. Так как denj соответствует обратимому обмену между системой и средой теплотой и веществом, то можно записать
В закрытой системе по де Донде
причем diS и есть теплота по Клаузиусу во втором начале термодинамики. Ранее отмечено, что diS ³ 0. Так же ранее записывали равенство, которое повторим в силу его определяющего значения dS = deS + diS,
Для закрытой системы denj = 0. Скорость химической реакции по j-му компоненту определяется величиной dnj/dt, тогда производство энтропии равно
Химическое сродство Пусть протекает химическая реакция Х + У ⇄ 2Z –dnX = –dnУ = 2dnZºdx x – полнота протекания реакции. dx – изменение степени полноты протекания реакции. Учитывая уравнения (35) и (36), запишем:
где
Для принятой или любой другой химической реакции подобного ттипа mX + mУ – 2mZºА, где А – химическое сродство, которое и является движущей силой химической реакции. Если химическое сродство не равно нулю, то система находится вне термодинамического равновесия и реакция протекает до А = 0.
В состоянии равновесия А = 0. Для химической реакции, записанной в наиболее общем виде а1А1 + а2А2 + а3А3 + … + аjАj = b1B1 + b2B2 + b3B3 + … + bkBk –a1dn(A1) = –a2dn(A2) = –a3dn(A3) = –ajdn(Aj) = = b1dn(B1) = b2dn(B2) = b3dn(B3) = bkdn(Bk), а химическое сродство А равно

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 .
. . (35)
. (35)


 .
. ,
,
 . (36)
. (36) .
. ,
, .
.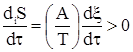
 – термодинамическая сила,
– термодинамическая сила,  – термодинамический поток.
– термодинамический поток. .
.