
|
|
Второе начало термодинамикиПервое начало термодинамики, давая строгое описание изменения энергии любой системы в результате ее обмена энергией с окружающей средой в форме теплоты или работы, не дает какого-либо критерия для разделения процессов на самопроизвольные и несамопроизвольные. Следовательно, оно не предоставляет критериев, предсказывающих направление процессов в природе. Нужен дополнительный или дополнительные критерии, не связанные с 1-м началом термодинамики, позволяющие оценить направление самопроизвольного течения процесса. Целесообразно было найти единый подобный критерий для всей возможной совокупности процессов. Прежде, однако, был сформулирован постулат, определяющий условия неосуществимости самопроизвольных процессов. В качестве такого постулата Р. Клаузиус предложил следующий. В природе неосуществим процесс перехода теплоты от менее нагретого года к более нагретому. В. Кельвин предложил иное выражение. В природе не осуществим такой замкнутый процесс, единственным результатом которого является совершение и переход теплоты от холодного тела к горячему. Эти постулаты представляют собой формулировку второго начала термодинамики. Наиболее интересная для химических целей формулировка второго начала термодинамики выражается через энтропию S – новую термодинамическую функцию, которую ввел Р. Клаузиус (1865 г.). Если имеется два состояния системы А и В, то в случае обратимого процесса SB – SA = или dS = Если T = const, то DS = Q/T. Размерность энтропии идентична размерности теплоемкости. Но если последняя – отношение теплоты к приращению температуры, то [S] - отношение теплоты к абсолютной температуре. Выражается энтропия в энтропийных единицах (э.е.) с размерностью Дж/моль×град. Абсолютное значение энтропии на основании первого и второго начал термодинамики получить невозможно, ибо при интегрировании выражения dS = получаем
где S0 – константа интегрирования, численное значение которой не удается определить. Учитывая, что в отсутствии химического превращения справедлива зависимость dQ = dU + pdV, то, подставив ее в уравнение (26), получим
Учтем, что в неравновесном процессе
так как q < Q. Отношение S2 – S1 = DS нельзя воспользоваться экспериментально найденными тепловыми эффектами, сопровождающими процессы, протекающие необратимо. Величина DS может быть только рассчитана на базе теплот равновесных процессов, приводящих к тому же состоянию. Энтропия как критерий самопроизвольного течения процесса Вернемся к уравнению
Зная на основании расчета изменение энтропии, можно определить направление протекания процесса в изолированной системе (масса вещества и энергия системы постоянны). Если систему изолировать, то dQ = 0 и DS = 0. Следовательно, в такой системе при равновесии энтропия остается постоянной. Для неравновесного процесса (вдали от равновесия)
так как q < Q. Следовательно, если такой процесс протекает в изолированной системе, то dq = 0 и
Таким образом, необратимый процесс в изолированной системе приводит к возрастанию энтропии. Отсюда следует вывод, что в изолированной системе самопроизвольно могут протекать только процессы, которые сопровождаются возрастанием энтропии. И идти такие процессы самопроизвольно могут только до такого состояния, при котором энтропия системы максимальна для конкретных рассматриваемых условий (рис. 22).
Рис. 22. Влияние характера изменения энтропии системы на возможность самопроизвольного течения процессов.
Под кривой рис. 22 заштрихована область самопроизвольного протекания процессов. Расчет энтропии Так как энтропия является экстенсивной величиной, то при наличии нескольких частей единой системы имеет место равенство
Кроме того, отметим, что, если процесс протекает при T = const, то Задача. Система состоит из двух кусков металла, практически не меняющих свою температуру при передаче некоторого количества теплоты Q от первой его части ко второй. Оценить возможность передачи тепла в следующих случаях: T1 > T2; T1 = T2; T1 < T2. 1. T1 > T2;
2. T1 = T2
3. T1 < T2
Если при протекании процесса в системе наблюдается изменение температуры, то DS находят интегрированием уравнения

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
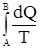
 .
.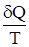
 , (26)
, (26) .
. ,
, называется приведенной теплотой. Тогда сумма приведенных теплот при реальном переходе системы из начального состояния в конечное меньше изменения энтропии, отвечающего этому переходу. Следовательно, для расчета разности
называется приведенной теплотой. Тогда сумма приведенных теплот при реальном переходе системы из начального состояния в конечное меньше изменения энтропии, отвечающего этому переходу. Следовательно, для расчета разности .
. ,
, ; S2 – S1 > 0 и DS > 0.
; S2 – S1 > 0 и DS > 0.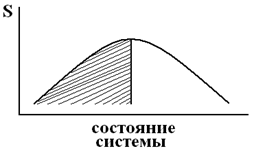
 .
. . Иначе говоря, расчет изменения энтропии в этом случае предельно прост. Рассмотрим. Рассмотрим пример.
. Иначе говоря, расчет изменения энтропии в этом случае предельно прост. Рассмотрим. Рассмотрим пример.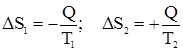 ;
;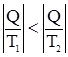
 ; процесс возможен.
; процесс возможен. ; достигнуто равновесие.
; достигнуто равновесие. ; процесс передачи теплоты невозможен.
; процесс передачи теплоты невозможен. .
.