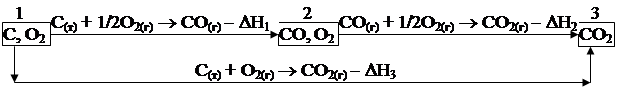|
|
Теплоемкость при постоянном давленииВыразим зависимость энтальпии от температуры
Отсюда dH = CpdT. Найдем соотношение между Cp и CV для идеального газа, учтя уравнение (17) и наличие в этом случае равенства
Их разность равна Cp - CV = Cp - CV = Так как для одного моля идеального газа pV = RT, то Cp - CV = Откуда Cp - CV = Cp - CV = R. 4. Адиабатический процесс, dQ = 0. Исходя из уравнений (10) и (14) CVdT + pdV = 0. С учетом связи p с V для идеального газа имеем
lnT + lnT + Обозначим отношение Ср/CV через g, тогда имеем lnT + ln(V)g-1 = const1 ln(TVg-1)= const1. Далее, опускаем индекс TVg-1 = const. Для 1 моля идеального газа справедлива зависимость pV = RT, то
Тогда
и окончательно имеем pVg = const. Задача. Как изменится произведение pV для СО2 при постоянном давлении, если объем увеличивается вдвое и g = 1,304? Вначале имеем произведение
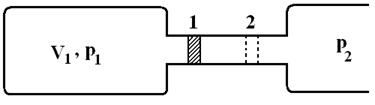
Равновесные процессы. Максимальная работа Ранее отмечалось, что при расширении газ производит работу только в том случае, если при этом он преодолевает сопротивление. Пусть имеется цилиндр с поршнем, который наполнен идеальным газом при некотором давлении р1. Объем цилиндра V1. Пусть при расширении поршень сместился из исходного положения 1 в положение 2. При этом объем газа увеличился на величину DV. Естественно произошло уменьшение давления. Но если
Причем, чем больше р2, тем больше и производимая им работа. Но возрастание р2 не беспредельно. Дело в том, что при р2 < р1 поршень будет двигаться в обратном направлении и работа будет производиться не системой, то есть газом в объеме V1, а над системой. Иначе говоря, она изменит свой знак. Следовательно, максимальная работа, производимая газом наблюдается при р1 = р2 равна р2DV. Причем сама система в этом случае находится в равновесии. Следовательно, в реальных условиях р1 всегда больше р2 и никогда нельзя получить максимальную работу, равную
где n – число моль газа, а R – универсальная газовая постоянная. Так как в случае идеального газа
Аmax никогда реально получить нельзя, но знать ее очень важно, так как она является мерилом качества использованных возможностей тепловой машины. Вместе с тем, все реальные процессы, протекающие с конечной скоростью необратимы, так как их движущая сила всегда больше преодолеваемой. (Скорость протекания равновесных процессов бесконечно мала, а сами они протекают бесконечно большое время). Воображаемый процесс, протекающий при р1 = р2, представляет собой непрерывный ряд равновесий. Такие процессы, называемые равновесными, протекающими с одинаковой вероятностью слева направо и наоборот. Термохимия Все химические реакции сопровождаются тепловыми эффектами. Более того, при некоторых фиксированных условиях протекания эти эффекты являются характеристическими величинами. Так, например, как было показано выше, при протекании изохорической химической реакции вся подводимая и отводимая от системы теплота ведет к изменению внутренней энергии системы, абсолютную величину которой оценить нельзя, но определение ее изменения в процессе химической реакции вполне возможно. При протекании процессов при постоянном давлении, подводимая к системе или отводимая теплота равна изменению ее энтальпии. При этом DH и DU равны только при сугубо частных условиях. Кроме того, абсолютные величины тепловых эффектов химических реакций (поглощение или отвод от системы теплоты в процессе их протекания) являются функциями температуры. И только в весьма узких температурных интервалах они могут быть приняты, в первом приближении, как постоянные. В связи со сказанным необходимо стандартизовать условия протекания химических процессов, то есть договориться об условиях, при которых вещества находятся в стандартном состоянии. За стандартные приняты следующие условия: температура 298 К или 25 °С; давление газа 1,035 × 105 Па; жидкости в стандартном состоянии находятся при том же давлении (или 1 атм). Если при протекании реакций происходит выделение теплоты, то изменение энтальпии (DH) отрицательно. Такие процессы называются экзотермическими (DH < 0). А + В ® С – DH В обратном случае (поглощение теплоты) DH положительно, а реакции называются эндотермическими (DH > 0). А + В ® С + DH Нолик, если он приводится, в верхнем индексе DH0 указывает на стандартное состояние всех участников реакции. Представленная выше условная система получила название термодинамической. В научной практике все термодинамические константы в справочниках приводятся при стандартных условиях. Для различных соединений характерны свои теплоты образования. Под теплотой (энтальпией) образования понимают количество теплоты, которое выделяется или поглощается при образовании 1 моля i-того вещества при рассматриваемых (в справочниках – стандартных) условиях из простых, термодинамически устойчивых веществ. При стандартных условиях их принято обозначать DH С + 1/2О2 = СО; DH 1/2Cl2(г) ® 1/2Cl2 + е ® Cl-; DH 1/2Cl2 + е + aq ® Cl C + 2H2 ® CH4(г); DH 6C + 3H2 ® C6H6(г); DH 5C + 6H2 ® C5H12(г); (н-пентан) DH Теплоты образования простых веществ, термодинамически стабильных, при стандартных условиях приняты условно равными нулю. Так, DH Кроме того, теплоты образования вещества зависят от его агрегатного состояния. DH DH DH В химической термодинамике широко используется понятие теплоты сгорания. Под теплотой сгорания вещества понимают то количество теплоты, которое выделяется при полном сгорании одного моля вещества до высших оксидов при данных условиях, учитывающих давление и температуру. Сгорание следует считать полным, когда C, H, N, S, Cl, входящих в состав химических веществ, превращаются соответственно в СО2, Н2О(ж), N2, SO2 и HCl. Под стандартной теплотой сгорания понимают DH Таким образом, стандартные теплоты образования и сгорания веществ, в том числе и органических можно считать их характеристическими константами. Закон Гесса До проведения работ Гесса было показано (А. Лавуазье), что количество теплоты, поглощаемое в прямой химической реакции, равно количеству теплоты, выделяющемуся в обратной реакции. Однако более широко связи между теплотой химической реакции и ее природой подробно исследовал Гесс. Он провел широкую серию экспериментов по нейтрализации кислот, измеряя при этом количество выделяющейся кислоты. Опубликованные им в 1840 г. результаты легли в основу закона, названного его именем. Сам автор его формулировал следующим образом: «Количество тепла, выделяющееся при образовании любого данного соединения, постоянно, независимо от того, образовалось ли это соединение прямо или окольным путем, за один шаг или за серию шагов». Современная формулировка этого закона следующая: «Тепловой эффект химической реакции не зависит от пути протекания процесса, а определяется только начальным и конечным состоянием системы (состоянием исходных веществ и продуктов реакции)». Это можно проиллюстрировать схемой, где в позициях (1) и (2) показаны исходные продукты первой и второй последовательных стадий, которые могут быть разделены большим промежутком времени, а над стрелками приведены собственно суммарные процессы с указанием их тепловых эффектов DHi.
Ниже показан тот же суммарный процесс, но протекающий в одну стадию и его тепловой эффект. В соответствии с законом Гесса должно соблюдаться равенство DH1 + DH2 = DH3, естественно с учетом знака. Действительно, экспериментально имеем: DH1 = 124,3 кДж; DH2 = 284,9 кДж; DH3 = 409,2 кДж. Геннадий Иванович Гесс (07.08.1802 – 12.12.1850) – академик Петербургской Академии наук (с 1830 г.), родился в Женеве, окончил Дерптский университет, совершенствовал свое образование в Стокгольмском университете. Один из основоположников термохимии. Сформулировал в 1840 г. положение, согласно которому величины тепловых эффектов химических реакций могут служить мерой химического сродства. Открыл (1840 г.) основной закон термохимии, названный его именем. Сформулировал закон электронейтральности, согласно которому смешение нейтральных солевых растворов не сопровождается тепловым эффектом. Впервые экспериментально доказал, что при нейтрализации моль-эквивалента любой сильной кислоты сильным основанием всегда выделяется одинаковое количество теплоты (определяемое теплотой образования моль-эквивалента воды Н+ + ОН- ® НОН). Открыл четыре новых минерала: вертит, уваровит, гидроборацит, фольбортит. Разработал способ получения теллура из теллурида серебра, впервые им же изученного минерала. Автор учебника «Основания чистой химии» (1831 г.), выдержавшего семь изданий.
Закон Гесса – следствие из 1-го начала термодинамики, сформулированного двумя годами позднее. Теперь появилась необходимость более строго сформулировать понятие теплового эффекта химической реакции. Согласно К.С. Краснова с соавторами, под тепловым эффектом химической реакции понимается количество теплоты, которое выделяется или поглощается при следующих условиях: - процесс протекает необратимо при р = const или V = const; - в системе не совершается никаких видов работ, кроме работы расширения; - продукты реакции имеют ту же температуру, что и исходные вещества. Но, так как QV = DU, а Qp = DH и U и H – функции состояния, то в этих случаях QV и Qp – также функции состояния, что и обусловливает закона справедливости Гесса. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ;
; 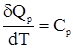 .
.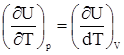 .
.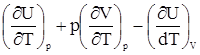
 .
. .
.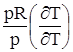 .
.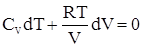
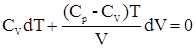
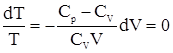
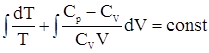
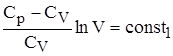
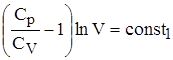 .
. .
.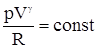
 , которое изменяется до
, которое изменяется до  . Найдем величину отношения:
. Найдем величину отношения: .
.
 ,
, , то
, то .
. , где f - formation. Для ряда процессов они приведены ниже.
, где f - formation. Для ряда процессов они приведены ниже. ; DH
; DH  ; DH
; DH  реакции, когда исходные вещества и продукты сгорания до высших оксидов находятся в стандартном состоянии.
реакции, когда исходные вещества и продукты сгорания до высших оксидов находятся в стандартном состоянии.