|
|
Понятия и термины химической термодинамикиСистема – это одно из базовых понятий. Под ним в термодинамике понимается тело или группа тел, находящихся во взаимодействии и мысленно обособленных от окружающей среды. Требование, предъявляемое термодинамикой к системе, состоит в том, что она должна состоять из большого числа образующих ее частиц, хотя их минимальное количество и не определено. Иначе говоря, система должна быть макроскопической. Таким образом, одна молекула не может представлять собой систему, это обязательно большая совокупность молекул. Такой подход ставит целью ряд вопросов: 1. В частности, может ли наночастица, состоящая из определенного числа атомов и молекул рассматриваться как термодинамическая система, к которой применимы положения термодинамики? 2. Может ли отдельный кластер, как совокупность образующих его атомов, молекул или каких-либо еще ассоциатов, представлять собой термодинамическую систему? По-видимому, в том и в другом случае ответ должен быть отрицательным. Но если система состоит из большой совокупности наночастиц и кластеров, то она, безусловно, как любая макроскопическая система, подчиняется положениям термодинамики. Если вводится понятие системы, то такое образование должно существовать не само по себе, а внутри некой окружающей среды, с которой, впрочем, оно может взаимодействовать определенным образом. Причем отсутствие взаимодействия следует рассматривать частным случаем его наличия. Исходя из этих соображений, можно представить три варианта термодинамических систем: 1. Открытая. 2. Закрытая. 3. Изолированная. Под открытой понимается система, которая способна обмениваться с окружающей средой веществом и энергией. Представим себе некоторый объем теплой жидкой воды, который находится в открытом сосуде. Из жизненного опыта людей следует, что такая система будет обмениваться веществом и энергией с окружающей средой. Масса воды во времени будет уменьшаться в результате испарения, а температура – понижаться за счет передачи энергии в форме теплоты окружающей более холодной среде. Меняя условия существования системы, можно направить эти обмены в обратном направлении. Закрытая система не обменивается с окружающей средой веществом, но обменивается энергией. Этот случай легко представить себе в виде абсолютно герметичной емкости, стенки которой не пропускают жидкую воду и ее пары, но обладают хотя бы малой теплопроводностью. Это определяет наличие обмена такой системой энергией с окружающей средой. Изолированная (от окружающей среды) система (хотя и находится в ней) не способна обмениваться, как, вероятно, уже догадался заинтересованный читатель, не способна к обмену ни веществом, ни энергией. Этот случай будет иметь место применительно к рассматриваемой нами системе, если вода будет находиться в герметичном сосуде, стенки которого образованы некоторым идеализированным материалом с нулевым коэффициентом теплопроводности. По другой классификации система может быть: 1. Гомогенной. 2. Гетерогенной. Гомогенная система состоит из одной фазы (например, пары воды в герметичном сосуде) и естественно не имеет границы раздела фаз. Совершенно очевидно, что одна фаза не может иметь внутри системы границы раздела. В этом случае такая граница существует только между системой и окружающей средой. Гетерогенная система состоит из нескольких фаз, отделенных одна от другой границей раздела. Например, если герметичный сосуд заполнен лишь частично жидкой водой, то над жидкой фазой обязательно находится паровая фаза (пары воды, то есть газ). Совершенно очевидно, что между этими фазами в такой однокомпонентной (Н2О) гетерогенной системе имеется граница раздела. В частности, на ней непрерывно протекают процессы испарения и конденсации. Любая система всегда находится в определенном состоянии. Причем, очевидно, что одна и та же система отличается чем-то, находясь, например, в состоянии I от ее же в состоянии II. Если таких различий не будет, то невозможны и два разные состояния единой системы. Следовательно, должны быть совершенно конкретными свойства системы. Термодинамические свойства системы должны быть взаимосвязаны. То есть при изменении одного из них претерпевают изменения и другие. Для полного описания состояния системы необходим минимальный набор термодинамических свойств. В термодинамике состояние системы описывается в терминах макроскопических переменных состояний. К ним относят: 1. Давление, р. 2. Объем, V. 3. Температура, Т. 4. Число моль компонентов системы, n. Термодинамической система называется в том случае, если ее состояние описывается посредством термодинамических параметров состояния. В свою очередь, термодинамические параметры состояния связаны между собой уравнением состояния. Для указанных выше параметров при ni = const, принимая систему однокомпонентной, уравнение состояния в самой общей форме имеет вид f(p, V, T) = 0. Для частного случая идеального газа уравнение состояния представляет собой уравнение Менделеева-Клапейрона, которое для одного моля любого газа имеет вид pV = RT для n молей одного компонента системы выражение несколько усложняется pV = nRT. И, наконец, для многокомпонентной системы с i-числом веществ оно записывается в следующем виде
Термодинамические свойства системы являются функциями состояния, то есть их изменение определяется исходным и конечным состоянием и не зависит от пути перехода из одного состояния в другое. Термодинамические переменные, в свою очередь делятся на два типа: 1. Интенсивные. 2. Экстенсивные. Интенсивные переменные, а к ним относятся температура и давление, не зависят от размеров системы. Они в равновесном состоянии системы одинаковы во всех ее точках. Так, если температура в разных точках системы различна, то теплота будет перетекать между ними до тех пор, пока этот параметр не выровняется, а система достигнет теплового равновесия. Забегая несколько вперед, отметим, что в состоянии теплового равновесия внутренняя энергия (U) и энтропия (S) однокомпонентной системы определяются полностью значениями Т, V и n, то есть U = U(T, V, n); S = S(T, V, n). Экстенсивные переменные зависят от размеров системы и пропорциональны ее массе. К ним относятся, внутренняя энергия системы, ее объем, энтропия, теплоемкость. Например, если систему разделить на несколько частей независимо от их размеров, то для ее внутренней энергии можно записать
Экстенсивные переменные U, S могут быть функциями других экстенсивных переменных U = U(S, V, n); S = S(U, V, n). Ниже будет показано, что интенсивные переменные могут быть представлены как производные одной экстенсивной переменной по другой, так Рассмотрим еще одну классификацию систем, по которой их также делят на два типа. 1. Равновесные системы. 2. Неравновесные системы. В случае изолированной системы ее состояние определяется макроскопическими переменными р, T и ni, которые во времени необратимо изменяются до достижения неизменного состояния. По его достижении далее в системе не наблюдается никаких физических и химических изменений. Система в этом случае достигает состояния термодинамического равновесия. Причем эволюция любого исходного состояния системы до равновесного происходит в результате необратимых процессов, которые с достижением равновесия прекращаются. Нулевое начало термодинамики. Пусть система А находится в равновесии с системой В. А система В в свою очередь с системой С. Тогда можно утверждать, что система А находится в равновесии с системой С. Этот вариант называют нулевым началом термодинамики. Заключая, отметим, что в случае равновесных систем имеет место равномерное распределение (постоянство) температуры. И для них имеются функции состояния – U и S. Для неравновесных систем, температура которых T = const, но локально, тем не менее, определена, согласно Л. Пригожина и Д. Кондепуди, можно предложить иной подход. Для них следует ввести плотности термодинамических величин U и S. Обозначим их теми же прописными буквами. Тогда плотность энергии u(T, ni(х)) = внутренняя энергия на единицу объема. ni(х) – молярная плотность – число молей на единицу объема. Тогда имеем
Термодинамические процессы. Физические или химические процессы, в которых участвует система, могут протекать при различных условиях. В соответствии с этим они классифицируются следующим образом. 1. Объем системы при протекании такого или таких процессов остается постоянным, то есть DV = 0, а сам процесс называется изохорическим. 2. Постоянным во времени остается давление, то есть Dр = 0. Имеет место изобарический (изобарный) процесс. 3. Постоянной во времени остается температура, DТ = 0. Процесс называется изотермическим. 4. Система не обменивается теплотой с окружающей средой, то есть Внутренняя энергия Рассмотрим систему, которая находится в некотором состоянии С (рис. 19). В координатах р, V она характеризуется некоторым объемом V и давлением р. В силу определенных причин, которые здесь не рассматриваются, так как их природа ничего не определяет, система переходит в состояние D. В состоянии С для нее характерно давление р1 и объем V1. В состоянии D - соответственно р2 и V2. Путь перехода системы из С в D показан сплошной линией I. Затем система возвращается в исходное состояние по маршруту II, совершая тем самым циклический или круговой процесс. Согласно закону сохранения энергии, система, вернувшаяся в исходное состояние, обладает тем запасом энергии, как и перед совершением циклического процесса. При этом, переходя по маршруту I, система получала теплоту Q и совершала определенную работу А. На маршрутах I и II полученная теплота и совершенная работа могут быть как положительными, так и отрицательными. Знаки их совершенно условны. В термодинамике положительной принимается теплота, поглощаемая системой и совершаемая ей работа. Напротив, отдаваемая системой теплота и работа, совершаемая над нею (например, работа сжатия газа) отрицательны. Следовательно, раз в циклическом процессе энергия системы не изменяется, то можно записать
где
Рис. 19. Схема циклического процесса.
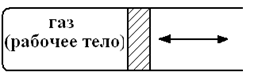
Рис. 20. Схематическое движение поршня в цилиндре двигателя тепловой машины.
Однако, вернемся к рис. 19. Система может переходить из состояния С в состояние D различными маршрутами, показанными пунктиром. Точно также по различным маршрутам из состояния D она может возвращаться в состояние С. Эти маршруты обозначены через III и IV. Пусть на i-том маршруте система получала количество теплоты Qi и совершала работу Ai (знаки Qi и Ai здесь не имеют смысла и не оговариваются). Тогда с учетом кругового процесса имеем Q1 + Q2 = A1 + А2 (2) Индекс, показанный арабской цифрой, соответствует номеру маршрута, указанному ранее римской цифрой. Из уравнения (2) следует Q1 - A1 = А2 - Q2 (3) Если учесть при протекании циклического процесса маршруты I и III, будем иметь Q1 - A1 = А3 - Q3 (4) Соответственно для прямого (I) и обратного (IV) маршрутов можно записать Q1 - A1 = А4 - Q4 (5) Из сопоставления уравнений (3), (4) и (5) следует, что (опуская индексы) в циклическом процессе: A – Q = const1 (6) Q – A = const2 (7) Величина постоянной в уравнениях (6) и (7) может иметь различные знаки: 1. Q > A, const2 > 0 (8) 2. Q < A, const2 < 0 (9) 3. Q = A, в частном случае, который вполне вероятен. Следовательно, исходя из первого случая (8), не вся полученная теплота может переходить в работу, то есть тратиться на совершение работы и, наоборот (из второго случая (9)), следует, что система может совершать бóльшую работу, чем полученная ею эквивалентная теплота. Избыток теплоты поглощается системой, что приводит к понятию внутренней энергии системы и которая в этом случае возрастает или дополнительная к Q совершенная системой работа выполняется за счет ее внутренней энергии. Способы передачи энергии. Из сказанного следует, что энергия может передаваться любой неизолированной системой в виде теплоты, а мера переданной энергии системой окружающей среды называется количеством теплоты. Следовательно, теплота связана с процессом, а не с состоянием системы. Поэтому она не является функцией состояния и зависит от характера процесса. Ранее количество теплоты было обозначено через Q, тогда бесконечно малое количество теплоты обозначим через dQ. Следовательно, dQ не является полным дифференциалом, так как Q не является функцией состояния. Помимо передачи в форме теплоты энергия может передаваться в виде работы, то есть обмен энергией между системой и окружающей средой может происходить в форме работы (системы или над системой). Работа в виде механического линейного перемещения равна dА = -Fldl. Fl – величина силы, совпадающая с направлением перемещения, dl - бесконечно малая величина перемещения. Работа против силы тяжести dА = -Fhdh. Fh – сила тяжести, dh – бесконечно малая высота поднятия тела. Работа расширения газа dА = pdV, р – внешнее давление, dV – бесконечно малое изменение объема. Отметим, что при расширении газа в пустоту (р = 0) работа также равна нулю (dА = 0), то есть чем больше сопротивление (р), тем больше совершаемая системой (газом) работа. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 .
. .
.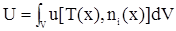
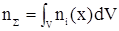
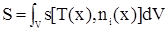
 , (1)
, (1) и
и 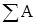 - соответственно вся теплота (принимаемая и отдаваемая) и вся работа (совершаемая системой и над системой). Например, при расширении газа в цилиндре двигателя (рис. 20), когда поршень движется слева направо, работа положительна, так как она совершается газом (рабочим телом, выступающим в роли системы) при его расширении. В обратном случае, когда поршень движется в обратном направлении справа налево под действием внешних сил, работа отрицательна. Уравнение (1) показывает, что невозможно построить машину, в процессе работы которой увеличивалась бы энергия системы, повторяя один и тот же цикл (процесс) многократно. Иначе говорят так: «Двигатель первого рода невозможен». Отсюда и другая формулировка: «Разные формы энергии переходят одна в другую в строго эквивалентных количествах».
- соответственно вся теплота (принимаемая и отдаваемая) и вся работа (совершаемая системой и над системой). Например, при расширении газа в цилиндре двигателя (рис. 20), когда поршень движется слева направо, работа положительна, так как она совершается газом (рабочим телом, выступающим в роли системы) при его расширении. В обратном случае, когда поршень движется в обратном направлении справа налево под действием внешних сил, работа отрицательна. Уравнение (1) показывает, что невозможно построить машину, в процессе работы которой увеличивалась бы энергия системы, повторяя один и тот же цикл (процесс) многократно. Иначе говорят так: «Двигатель первого рода невозможен». Отсюда и другая формулировка: «Разные формы энергии переходят одна в другую в строго эквивалентных количествах».