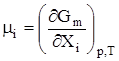|
|
Термодинамические потенциалыОценка возможности самопроизвольного прохождения различных процессов, в том числе и химических взаимодействий, может быть сделана не только на основе расчета изменения энтропии, но и ряда других критериев, называемых термодинамическими потенциалами. В качестве одного из критериев может быть избрана работа, так как при самопроизвольном протекании процесса она только положительна. Если работа отрицательна, то, как отмечалось ранее, она производится над системой, а не системой. Такой процесс, конечно, не является самопроизвольным. Работа, как критерий самопроизвольного течения процесса, удобна и тем, что она поддается измерению. Но у нее есть и серьезный недостаток – она не является функцией состояния, то есть зависит от пути прохождения процесса. Это легко понять, учтя, что при переносе кирпичей из одной комнаты в другую можно пройти кратчайшим путем. Но с другой стороны, с этими же кирпичами можно обойти весь земной шар и лишь затем попасть в нужную комнату. Очевидно, что в том и в другом случаях работа существенно различно. Указанный недостаток необходимо преодолеть. Целесообразно необходимо найти некий параметр, являющийся функцией состояния, изменение которого можно выразить через совершенную системой работу. Такой параметр и будет служить в качестве критерия для решения вопроса о возможности или невозможности самопроизвольного течения процесса. Для его нахождения используем 1-е и 2-е начала термодинамики dQ = dU + dA. С учетом последнего начала имеем dA = TdS – dU. Примем, что процесс протекает в изотермических условиях (T = const). Интегрирование последнего уравнения
дает A = (TS2 – TS1) – (U2 – U1); A = (U1 – TS1) – (U2 – TS2). Разность U – TS обозначим через F. Тогда F = U – TS, (359) F –решением международного союза по чистой и прикладной химии называется свободной энергией Гельмгольца или изохорно-изотермическим потенциалом. Отметим, что все эти преобразования имеют место в рамках равновесной термодинамики. F является функцией состояния, так как ею являются определяющие ее внутренняя энергия и энтропия. A = –(F2 – F1) = –DF. Произведение TS характеризует связанную работу – часть внутренней энергии системы, которая при заданных условиях не может быть переведена в работу. А в рассматриваемом случае представляет интегральную работу системы, которая, ранее выраженная в дифференциальной форме, равна: dА = pdV + dA¢, где dA¢ – все остальные возможные виды работы, включая и работу химического превращения. Рассмотрим возможности свободной энергии Гельмгольца, как критерия самопроизвольного течения процесса, более детально. С этой целью продифференцируем уравнение (39) dF = dU – TdS – SdT. (40) Из первого начала термодинамики следует ¶Q = dU + pdV + dA¢. (41) Сочетая уравнения (40) и (41), получим с учетом выражения для 2-го начала термодинамики TdS = dU + pdV + dA¢; dU = TdS – pdV – dA¢. dF = TdS – pdV – dA¢ + TdS – SdT dF = – pdV – SdT – dA¢. (42) Легко видеть, что при T = const dF = – pdV – dA¢, а при T = const и V = const dF = – dA¢. (43) Таким образом, при указанных условиях A¢ обладает свойствами функции состояния. При T = const и dA¢ = 0 dF выражает собой только работу расширения. Из уравнения (42) следует: 1) dA¢ = 0, dV = 0, тогда 2) dA¢ = 0, dТ = 0, тогда Перепишем уравнение (42) с учетом dA¢ как работы химического превращения dF = – pdV – SdT + Тогда Из уравнения (43) следует: 1. dF < 0 (F2 > F1) – самопроизвольный процесс возможен; 2. dF > 0 (F2 < F1) – самопроизвольный процесс невозможен; 3. dF = 0 (F2 = F1) – состояние равновесия. Следовательно, все самопроизвольные процессы идут в сторону уменьшения свободной энергии Гельмгольца. Пределом их протекания является достижения равновесия. Свободная энергия Гиббса Можно найти еще один термодинамический потенциал, обладающий свойствами функции состояния, характеризующий только dA¢ (максимально полезную работу). Используем тот же подход, примененный ранее для нахождения свободной энергии Гельмгольца. dQ = dU + pdV + dA¢; (44) TdS = dU + pdV + dA¢; (45) dA¢ = TdS – dU – pdV. (46) Проинтегрируем уравнение (46) A¢ = TS2 – TS1 – U2 + U1 – pV2 + pV1 A¢ = (U1 + pV1 – TS1) – (U2 + pV2 – TS2). Ранее указывалось, что U + pV = H. Тогда A¢ = (Н1 – TS1) – (Н2 – TS2). Разность H – TS обозначим через G. G называется свободной энергией Гиббса или изобарно-изотермическим потенциалом. G = U + pV – TS; (47) A¢ = –DG. A¢ приобретает свойства функции состояния, так как она является Н и S. Отсюда следует 1. G2 > G1, A¢ – отрицательна; 2. G2 < G1, A¢ – положительна; 3. G2 = G1, A¢ = 0. Следовательно, все самопроизвольные процессы идут в сторону уменьшения свободной энергии Гиббса. Продифференцируем уравнение (47) dG = dU + pdV + Vdp – TdS – SdT и сочетая его с уравнением (45), получим dG = TdS – pdV – dA¢ + pdV + Vdp – TdS – SdT. dG = – SdT + Vdp – dA¢. (48) Из уравнения (48) легко видеть, что при dT = 0 (T = const) и dp = 0 dG = –A¢. Заменим dA¢ через dG = – SdT + Vdp + Из последней зависимости имеем:
Для гомогенной системы U = TS – pV + и, кроме того, ранее показано, что G = U + pV – TS. Сочетая два последние уравнения, получим G = то есть свободную энергию Гиббса можно связать с химическим потенциалом. Для чистого вещества G = m × n; Иначе говоря, химический потенциал есть свободная энергия Гиббса, отнесенная к 1 молю чистого вещества. Для многокомпонентной системы, если уравнение (49) привести к 1 молю всех компонентов (разделить на полное число молей), получим
где Хi – мольная доля i-го вещества, mi – его химический потенциал. Gm – функция р, Т и ni, то
и mi = f(p, T, xi). Все параметры, характеризующие возможность самопроизвольного протекания процесса, собраны в таблице 20. Таблица 20 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
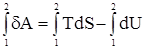
 ;
; .
. .
.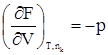 ;
;  и
и 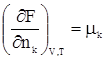 .
.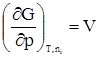 ;
; 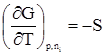 ;
; 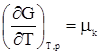 .
.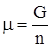 . (49)
. (49)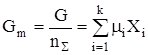 ,
,