
|
|
УЭ- 8 . Решение уравнений, сводящихся к квадратнымВаша цель: научиться решать уравнения. уравнения. сводящиеся к квадратным. Входная информация Рассмотрим некоторые подходы к решению уравнений высших степеней. Простейшие уравнения. сводящиеся к квадратным. Многие уравнений с помощью метода введения новой переменной можно свести к квадратному уравнению, к их системе или совокупности таких уравнений. Пример1. Решим уравнение Решение. Вводим новую переменную 1) Ответ: Пример 2. Решим уравнение
Решение. Введем подстановку Чтобы найти значения переменной x, нужно решить уравнения Ответ: –2; 1. Решение уравнений вида (x + a) (x + b) (x + c) (x + d) = т , где a + b = c + d (или а + с = b + d или a + d = b + c). Рассмотрим конкретный пример.
Пример 3. Решить уравнение (х + 4) (х + 5) (х + 7) (х + 8) = 4. Решение. Заметим, что 4 + 8 = 5 + 7. Перемножив в левой части уравнения выражения, стоящие в первой и четвертой скобках, а также выражения, стоящие во второй и третьей скобках, получим: Сделаем замену Таким образом, исходное уравнение сводится к совокупности уравнений:
Решая эту совокупность уравнений, получаем: Ответ: Решение уравнений вида
Итак, уравнение (x + a) (x + b) (x + c) (x + d) = т приводится к квадратному методом подстановки, если a + b = c + d (или а + с = b + d или a + d = b + c). Решение уравнений вида . Пример 4. Решить уравнение
Решение. Пусть х – 4,5 = y + k, х – 5,5 = у – k(*).Вычитая из первого равенства второе, получаем k = 0,5. Тогда х – 4,5 = у + 0,5, . х - 5,5 = = у– 0,5. Относительно у уравнение примет вид:
или Раскрывая скобки и приводя подобные члены, получим биквадратное уравнение:
Тогда из формул (*) находим решение исходного уравнения. Ответ: 4,5; 5,5. Итак, уравнение Пример 5. Решить уравнение
Решение. Введем подстановку х = у – 4 и данное уравнение перепишем так:
Выполним преобразования:
Откуда Из равенства х = у – 4 имеем: Ответ: –3; –5.
Метод выделения полного квадрата. Для решения некоторых уравнении, сводящихся к квадратным, используется метод выделения полного квадрата. Пример 6. Решим уравнение
Решение. В левой части данного уравнения выделим полный квадрат:
Введем подстановку Если у = 1, то Если у = 3, то Ответ: Метод разложения левой части на множители. Если левую часть уравнения вида f(x) = 0, где f(x)– многочлен удается разложить на множители, то решение такого уравнения сводится к решению совокупности алгебраических уравнений_меньшей степени. Заметим, что решить совокупность уравнений с одной переменной (f(x)= 0 или g(x) = 0) – значит найти все числа, являющиеся решением хотя бы одного уравнения, входящего в данную совокупность, или доказать, что таких чисел не существует. Совокупность уравнений f(x) =0 и g(x) = 0 символически можно записать так:
либо f(x) = 0 или g(x) = 0. Пример 7. Решить уравнение
Решение. Сгруппируем первые три члена уравнения и вынесем
Решений нет. Ответ:
Пример 8. Решить уравнение
Решение. Применив группировку, запишем уравнение в виде:
Выделим полные квадраты в каждой скобке, не нарушив равносильности уравнений:
Откуда имеем:
Полученное уравнение равносильно совокупности двух уравнений:
Корнями первого уравнения являются числа Ответ: Решение возвратных уравнений. Некоторые уравнения имеет особенность: коэффициенты, равноудаленные от начала и конца многочлена, стоящего в левой части уравнения, равны между собой. Уравнения с такой особенностью называются возвратными. На примере покажем способ решения возвратного уравнения третьей степени.
Пример 9. Решить уравнение
Решение. Применив группировку, запишем данное уравнение в виде:
т.е. откуда
Ответ: Заметим, что уравнение вида Практическая часть С некоторыми видами следующих заданий вы могли встречаться на уроках математики. Самоопределитесь, какие из следующих заданий вам необходимо выполнить. В случае затруднений обращайтесь к рубрике «Ваш помощник», за консультацией к учителю или за помощью к товарищу. Задание 1. Решите уравнение: а) б) . Задание 2. Решите уравнение, введя новую переменную: а) б) в) г) д) е) Задание 3. Решите уравнение: а) б) Задание 4. Решите уравнение: а) б) Задание 5. Решите уравнение: а) б) Задание 6. Решите уравнение методом введения новой переменной: а) б) в) г) д) Задание 7. Решите уравнение: а) б) в) Задание 8. Решите уравнение: а) б) Задание 9. Решите уравнение: а) б) Задание 10. Решите уравнение: а) б) в) г) д)

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 .
.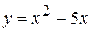 , тогда
, тогда 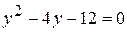 , откуда
, откуда  и
и 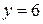 . Далее имеем:
. Далее имеем: , т.е.
, т.е.  . Его корни:
. Его корни: 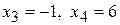 .
.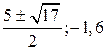 .
.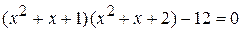 .
.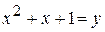 , тогда данное уравнение примет вид y (y + 1) – 12 = 0, т.е.
, тогда данное уравнение примет вид y (y + 1) – 12 = 0, т.е. 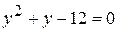 . Отсюда находим y = – 4 или y = 3.
. Отсюда находим y = – 4 или y = 3.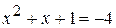 и
и 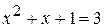 , после чего объединить их корни. Решая полученные квадратные уравнения, находим:
, после чего объединить их корни. Решая полученные квадратные уравнения, находим: 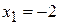 ,
,  .
.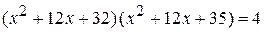 .
. . Тогда y (y + 3) = 4, или
. Тогда y (y + 3) = 4, или 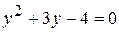 , откуда у = – 4 или y = 1.
, откуда у = – 4 или y = 1. или
или 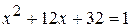 т.е.
т.е. или
или 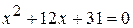 .
.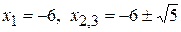
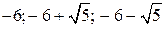 .
. . Рассмотрим конкретные примеры.
. Рассмотрим конкретные примеры.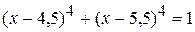 .
.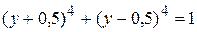 ,
, .
.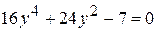 ,
,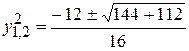 ;
; ;
;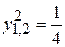 , т.е.
, т.е. 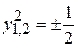 .
. .
.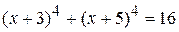 .
. .
. ,
,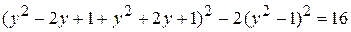 ,
, .
.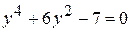 ,
,  или
или 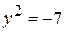 . Отсюда находим, что
. Отсюда находим, что 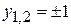 .
. или
или 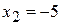 .
.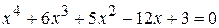 .
. ,
, .
.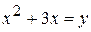 . Тогда относительно переменной у уравнение примет вид:
. Тогда относительно переменной у уравнение примет вид: 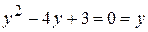 , откуда получаем: y = 1 и y = 3.
, откуда получаем: y = 1 и y = 3.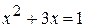 ,
, 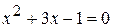 . Откуда находим:
. Откуда находим: 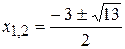
 ,. Откуда находим:
,. Откуда находим:  .
.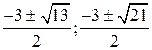 .
.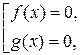
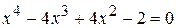 .
. за скобку:
за скобку: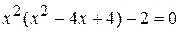 или
или 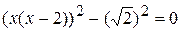 ;
; ,
, или
или 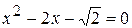 .
. .
.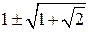 .
. .
.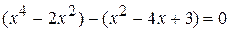 .
.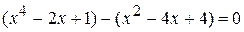 , т. е.
, т. е.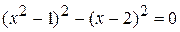 .
.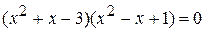 .
. или
или 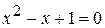 .
. , а второе уравнение решений не имеет.
, а второе уравнение решений не имеет. .
.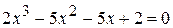 .
.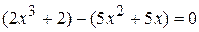 ,
, ,
,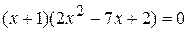 ,
,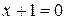

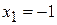
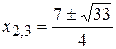 .
.
 .
.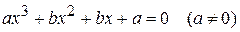 равносильно уравнению
равносильно уравнению 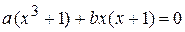 , т. е. уравнению
, т. е. уравнению 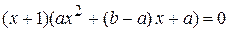 которое легко решается
которое легко решается ,
,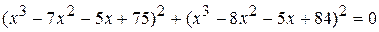
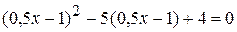 ;
;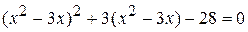 ;
;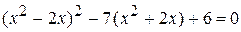 ;
;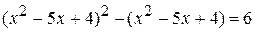 ;
;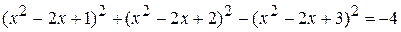 ;
;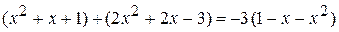 .
. ,
,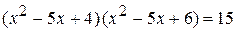 ;
; ,
, .
. 
 ;
;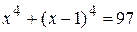 .
. ;
;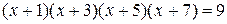 ;
;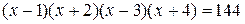 ;
;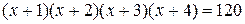 ;
; .
.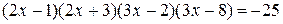 ;
;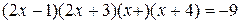 ;
;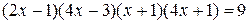 .
.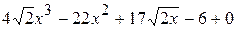 ;
;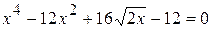 .
.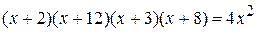 ;
;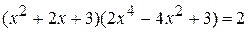 .
.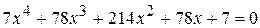 ;
; ;
;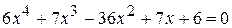 ;
;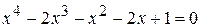 ;
;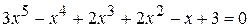 .
.