
|
|
УЭ-4. Модуль действительного числаВаша цель: четко знать определение модуля действительного числа; понимать геометрическую интерпретацию модуля действительного числа и уметь применять ее при решении задач; знать свойства модуля и уметь применять при решении задач; уметь представление о расстоянии между двумя точками координатной прямой и уметь использовать его при решении задач. Входная информация Понятие модуля действительного числа. Модулем действительного числа Модуль числа
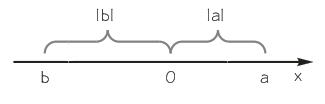
Геометрическая интерпретация модуля. Геометрически модуль действительного числа есть расстояние от точки, изображающей данное число на координатной прямой, до начала отсчета.
Решение уравнений и неравенств с модулями на основе геометрического смысла модуля. Пользуясь понятием «расстояние между двумя точками координатной прямой» можно решать уравнения вида Пример. Решим уравнение Решение. Переформулируем задачу геометрически. Поскольку Короче, на координатной прямой найти множество координат точек, расстояние от которых до точки с координатной 1 равно 2. Решим эту задачу. Отметим на координатной прямой точку, координата которой равна 1 (рис. 6) На две единицы от этой точки удалены точки, координаты которых равны -1 и 3. Значит, искомое множество координат точек есть множество, состоящее из чисел -1 и 3. Ответ: -1; 3. Как найти расстояние между двумя точками координатной прямой. Число, выражающее расстояние между точками Для любых двух точек
Основные свойства модуля действительного числа: 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. При 11. 12. 13. 14. 11. Практическая часть Задание 1. Возьмите чистый лист бумаги и на нем запишите ответы ко в сем устным упражнениям, приведенным ниже. Свои ответы сверьте с ответами или краткими указаниями, помещенными в конце учебного элемента в рубрике «Ваш помощник». 1. Раскройте знак модуля: а) |–5|; б) |5|; в) |0|; г) |p|. 2.Сравните между собой числа: а) || и –; в) |0| и 0; д) – |–3| и –3; ж) –4|а| и 0; б) |–p| и p; г) |–7,3| и –7,3; е) |а| и 0; з) 2|а| и |2а|. 3.Как при помощи знака модуля записать, что по крайней мере одно из чисел а, b или с отлично от нуля ? 4.Как при помощи знака равенства записать, что каждое из чисел а, b и с равно нулю ? 5. Найдите значение выражения: а) |а| – а; б) а + |а|. 6. Решите уравнение: а) |х| = 3; в) |х| = –2; д) |2х – 5| = 0; б) |х| = 0; г) |х – 3| = 4; е) |3х – 7| = – 9. 7. Что можно сказать о числах х и у, если: а) |х| = х; б) |х| = –х; в) |х| = |у|? 8. Решите уравнение: а) |х – 2| = х – 2; в) |х – 3| =|7 – х|; б) |х – 2| = 2 – х; г) |х – 5| =|х – 6|. 9.Что можно сказать о числе у, если имеет место равенство: а) ïхï = у; б) ïхï = –у ? 10. Решите неравенство: а) |х| > х; в) |х| > –х; д) |х| £ х; б) |х| ³ х; г) |х| ³ –х; е) |х| £ –х. 11.Укажите все значения а, для которых имеет место равенство: а) |а| = а; б) |а| = –а; в) а – |–а| =0; г) |а|а = –1; д) = 1. 12. Найдите все значения b, для которых имеет место неравенство: а) |b| ³ 1; б) |b| < 1; в) |b| £ 0; г) |b| ³ 0; д) 1 < |b| < 2.
С некоторыми видами следующих заданий вы могли встречаться на уроках математики. Самоопределитесь, какие из следующих заданий вам необходимо выполнить. В случае затруднений обращайтесь к рубрике «Ваш помощник», за консультацией к учителю или за помощью к товарищу. Задание 2. Исходя из определения модуля действительного числа, решите уравнение:
Задание 3. Укажите на координатной прямой множество таких точек, для которых справедливо соотношение:
Задание 4. Расстояние между точками, изображающими действительные числа α и β на координатной прямой, равно | α – β |. Пользуясь этим, решите уравнение:
Задание 5. Докажите, что а) Задание 6. Докажите, что Задание 7. Докажите, что: а) б) в) Рубрика «Ваш помощник» 1. а) 5; б) 5; в) 0; г) –p. 2. а) || > –; б) |–p| = p; в) |0| = 0; г) |–7,3| > –7,3; д) – |–3| = –3; е) если а = 0, то |а| = 0; если а ¹ 0, то |а| > 0. 3. |а| + |b|+ |с| ¹ 0 либо а2 + b2+ с2 ¹ 0. 4. |а| + |b|+ |с| = 0 либо а2 + b2+ с2 = 0. 5. а) Если а ³ 0, то |а| – а = 0; если а < 0, то |а| – а = –2а. 6. а) {–3; 3}; б) {0}; в) Æ; г) {–1; 7}; д) {2,5}; е) Æ. 7. а) х ³ 0; б) х £ 0; в) х = у или х = –у. 8. а) [2; +¥); б) (–¥; 2]; в) {5}; г) {5, 5}. 9. а) у ³ 0; б) у £ 0. 10. а) (–¥; 0); б) (–¥; ¥); в) (0; ¥); г) (–¥; ¥); д) [0; ¥); е) (–¥; 0].
11. а) а ³ 0; б) а £ 0; в) а ³ 0; г) а = –1; д) а > 0. 12. а) b £ –1 или b ³ 1; б) –1 < b < 1; в) b = 0; г) R; д) –2 < b < –1 или 1 < b < 2. К заданию 2. а) 1,5 ; б) 3,5; 4,5; в) 2.%; е) нет решений. К заданию 3. а) -2,4; б) -1; 4; в) 6; г) -0,5; 0,5; д) 0; 2. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 называют само это число
называют само это число  , и противоположны ему число
, и противоположны ему число  , если
, если  обозначают
обозначают  и записывают:
и записывают:
 или неравенства вида
или неравенства вида  , где вместо знака
, где вместо знака  может стоять любой из знаков
может стоять любой из знаков 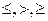 .
. .
. -это расстояние на координатной прямой между точками с координатами
-это расстояние на координатной прямой между точками с координатами  и
и  , значит, требуется найти координаты таких точек, расстояние от которых до точек с координатой 1 равно 2.
, значит, требуется найти координаты таких точек, расстояние от которых до точек с координатой 1 равно 2. и
и  , называют расстоянием между числами
, называют расстоянием между числами 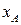 и
и  .
.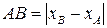 .
.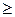 0;
0; ;
; ;
; ,
,  ;
; ;
; ;
; ;
; ;
; ;
; .
. имеем:
имеем: тогда только тогда, когда
тогда только тогда, когда  или
или 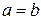 ;
; тогда только тогда, когда
тогда только тогда, когда 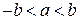 ;
; тогда только тогда, когда
тогда только тогда, когда  или
или 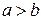 ;
; тогда только тогда, когда
тогда только тогда, когда  ;
; тогда только тогда, когда
тогда только тогда, когда  .
. ; б)
; б)  в)
в)  .
. тогда и только тогда, когда
тогда и только тогда, когда  .
. ;
; ;
;