
|
|
Уравнения, сводящиеся к квадратным уравнениям
УЭ-1. Понятие квадратного уравнения. Неполные квадратные уравнения Ваша цель:актуализация основных знаний, умений и навыков по данной теме, полученных на уроках математики. Входная информация Понятие квадратного уравнения. Одним из важнейших понятий школьного курса алгебры является понятие квадратного уравнения. Квадратным уравнением называется уравнение вида ах² + bх + с = 0, где х– переменная, а, b, с – некоторые действительные числа, причем а ≠ 0. Числа a, b и с – коэффициенты квадратного уравнения. Число а называют первым коэффициентом, b – вторым коэффициентом и с – своодным членом. Примеры квадратных уравнений:
Квадратное уравнение Из определения следует, что неполные квадратные уравнения могут быть трех видов: 1) 2) ax2+ c = 0, где c ≠0; 3) ax2+ bx = 0, где b ≠0. Учимся решать неполные квадратные уравнения. 1. Уравнение ах2= 0 имеет единственный корень х= 0. Поскольку а ≠≠0, а из ax2 = 0 следует, что x2= 0, и потому х = 0. 2. Уравнение ax2+ c = 0 (с ≠ 0) равносильно уравнению а) Если б) Если
Пример 1. Решим уравнение Решение. Перенесем свободный член в правую часть уравнения и разделим обе части получившегося уравнения на – 2: –2x² = – 14 x² = 7
Ответ: 3. Уравнение ax² +bx = 0(b≠ 0) равносильно уравнению х(ах+ b)= = 0, откуда Пример 2. Решим уравнение 5x² + 3x = 0. Решение. Разложим левую часть уравнения на множители: x(5x + 3)=0. Откуда x = 0 или 5x + 3 = 0, т.е. Ответ: – 0,6; 0. Практическая часть Задание 1. Возьмите чистый лист бумаги и на нем запишите ответы ко в сем устным упражнениям, приведенным ниже. Свои ответы сверьте с ответами или краткими указаниями, помещенными в конце учебного элемента в рубрике «Ваш помощник». Устные упражнения
1. Чему равен первый коэффициент, второй коэффициент и свободный член в уравнении: а) 3х2 – 4х + 5 = 0; в) 7х2 + 5 = 0; д) 3х – 8 + 6х2 = 0; б) –х2 + 3х = 0; г) х2 – 10 = 0; е) 7 – х2 = 0 ? 2.При каких значениях параметра а уравнение (а2 – 1)2х + 5х – 3 = 0 является квадратным ? 3.Каков план решения неполного квадратного уравнения: а) ах2 = 0; б) ах2 + bx = 0; в) ах2 + с = 0 ?
4.Какое из уравнений не имеет решений: а) х2 = 0; в) –3х2 = –p; д) 7х2 – 7 = 0; б) 3х2 = p; г) х2 + 25 = 0; е) х2 + 1 = 0 ? 5.Найдите корни многочлена: а) х2 – 10; б) х2 – 7х; в) 0,5х2 – 4х; г) 3х2 + 5х. 6.Докажите, что многочлен 3х2 + 2 не имеет корней. 7.При каких значениях с многочлен х2 + с не имеет корней ? 8.Решите уравнение: а) х2 – 10х + 25 = 0; в) 4х2 – 6х + 9 = 0; б) х2 + 6х + 9 = 0; г) 9х2 – 24х + 16 = 0;
9. Составьте уравнение, которое имеет два корня, сумма которых равна нулю. 10. Сколько корней может иметь уравнение: а) х2 = р; б) х2 = ïрï; в) х2 = –ïрï; г) х2 + 2 = –ïрï?
С некоторыми видами следующих заданий вы могли встречаться на уроках математики. Самоопределитесь, какие из следующих заданий вам необходимо выполнить. В случае затруднений обращайтесь к рубрике «Ваш помощник», за консультацией к учителю или за помощью к товарищу.
Задание 2. Является ли квадратным уравнение: а) б) 13x² – x + 8 = 0; д) 9x³ - 2x = 0•, в) 0 · x² + 5 – 4x = 0; е) – 0,5x² = 0 ? Задание 3.Найдите корни уравнения: а) 5x² – 45 = 0; г) –0,1y² + 40 = 0;•, б) – x² = 0; д) в)
Задание 4.Решите уравнение: а) 3x² – 5x = 0; г) б) –4x² – x = 0; д) в) Задание 5. Решите уравнение: а) 4x² + 6x = 9x² – 15x; в) 8,5x – 2x² = 3,5x + 3x² ; б) 12x + 6x² = 5x² – 7x; г) x (x – 6) = 3 (108 – 2х). Задание 6. Решите уравнение: а) x² = a; в) a² x² – 9 = 0; б) x² + a = 0; г)a² x² – ax = 0, где х – переменная, а – параметр. Задание 7. Решите уравнение: а) a(x² + x) = 0; б) где х – переменная, а, b, с – параметры. Задание 8.Напишите общий вид квадратного уравнения, в котором: а) один из корней равен нулю; б) оба корня равны нулю; в) корни равны по модулю, но противоположны по знаку.
Рубрика «Ваш помощник» К заданию 1. Ответы на устные упражнения; 1. а) а = 3, b = –4; с = 5; б) а = –1, b = 3; с = 0; в) а = 7, b = 0; с = 5; г) а = 1, b = 0; с = –10; д) а = 6, b = 3; с = –8; г) а = –1, b = 0; с = 7. 2. При всех а, кроме а = –1 и а = 1. 3. а) (ах2 = 0) Û (х2 = 0), откуда х1 = х2 = 0; б) (ах2 + bx = 0) Û (х(ах + b) = 0) Û (х = 0 или ах + b = 0), откуда х1 = 0, х2 = –; в) (ах2 + с = 0) Û (х2 = –): если – > 0, то х1,2 = ; если 4Уравнения г) и е) решений не имеют. 5. а) –; ; б) 0; 7; в) 0; 8; г) 0; –. 6. Доказательство: 3х2 ³ 0 при любом х, а 2 число положительное, значит 3х2 + 2 > 0 при любом х. 7. При c > 0. 8. а) х1 = х2 = 5; в) х1 = х2 = 1,5; б) х1 = х2 = –3; г) х1 = х2 = . 9. х2 – 5 = 0. 10. а) если р < 0, то данное уравнение действительных корней не имеет; если р = 0, то имеет два равных корня, т.е. х1 = х2 = 0; если р > 0, то уравнение имеет два корня, т.е. х1 = –, х2 = ; б) данное уравнение имеет два корня при любом р; в) если р = 0, то данное уравнение имеет два равных корня; если р ¹ 0, то корней нет; г) при любом р данное уравнение корней не имеет. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
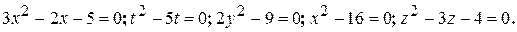
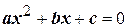 называется неполным, если коэффициент b или свободный член равен нулю.
называется неполным, если коэффициент b или свободный член равен нулю. =0;
=0;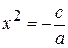 Возможны два случая.
Возможны два случая. < 0, то уравнение
< 0, то уравнение 
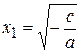 ,
, 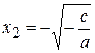
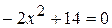 .
.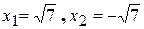 .
. .
.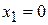 или
или 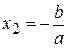 .
. .
. ; г) 3 – 16x = 0;
; г) 3 – 16x = 0;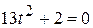 ;
; ; е)
; е) 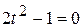 ;
;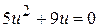 ; ж)
; ж) 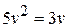 ;
; ; з)
; з) 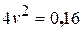 ;
;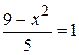 ; е)
; е) 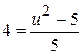 ; и)
; и)  .
.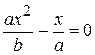 ; в) ах² – bх = сх²,
; в) ах² – bх = сх²,