
|
|
Квадратного корня из числаУже в древние времена решение задач практического характера (например, выделение квадратного участка земли заданной площади) приводило к необходимости извлечения квадратного корня из числа. Так, в китайской математической рукописи, написанной во II в. до н.э., имеется описание способа нахождения квадратных корней. Индийцы в IV – V вв. нашей эры умели извлекать квадратные корни из чисел. Индийский математик XII в. Бхаскара (1114 – позднее 1178) отмечал, что для каждого положительного числа можно указать два квадратных корня (положительный и отрицательный) и что нельзя извлечь квадратный корень из отрицательного числа. В сочинении знаменитого среднеазиатского математика аль-Хорезми (787 – ок. 850) встречается способ извлечения квадратного корня, например, при решении квадратных уравнений. Интересен способ, используя который древние вавилоняне находили приближенные квадратные корни еще за две тысячи лет до нашей эры. На современном алгебраическом языке этот способ может быть записан так:
Пример 1. Вычислим Так как
Поскольку Пример 2. Вычислим Используя формулу (1), получим:
Заметим, что Возведя правую часть равенства (1) в квадрат, получим:
Легко заметить, что квадрат найденного приближенного значения корня отличается от подкоренного числа на число У вавилонян не было знака для обозначения квадратного корня. Этот знак имеет свою историю возникновения и развития. Было время (XVI в.), когда знаком корня служила буква R, а рядом ставилась первая буква латинского слова «квадратный» (q). Например, писали Еще в древности возникала необходимость извлекать квадратный корень из отрицательного числа в задачах, решаемых с помощью квадратных уравнений. Однако в те времена считали такую задачу неразрешимой. В первой половине XVI в. поиск решений некоторых уравнений привел итальянских математиков к выражению действительных корней через квадратные корни из отрицательных чисел. Это заставило математиков того времени оперировать новыми числами, которые называли «мнимыми», «воображаемые» и т. д. В настоящее время их называют комплексными числами. Для таких чисел применяли правила действий, которым подчинялись действительные числа. Однако смысл новых чисел долгое время оставался непонятным. В начале XIX в. было дано их наглядное геометрическое изображение (как точек плоскости), и развитие теории комплексных чисел прошло успешно. С множеством комплексных чисел вы познакомились в старших классах. Интересные задачи 1.Легко проверить, что имеют место равенства:
Как записать в общем виде закономерность, которая в них проявляется? 2. Верны равенства:
Чему равно значение выражения 3. Задача индийского математика Б. Бхаскары «Докажите, что
Софизмы а) Докажем, что «Доказательство». Запишем верное равенство 16 – 36 = 25 – 45. Далее имеем:
Найдите ошибку в рассуждении. б) Докажем, что половина метра равна пяти сантиметрам. «Доказательство». Запишем верное равенство
Извлекая квадратный корень из обеих частей этого равенства, получим:
Объясните, почему так получилось. Мне приходится делить свое время между политикой и уравнениями. Однако уравнения, по-моему, гораздо важнее, потому что политика существует только для данного момента, а уравнения будут существовать вечно. А. Эйнштейн Модуль 4. Квадратные уравнения. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 . (1)
. (1)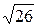 указанным выше способ.
указанным выше способ. , то по формуле (1) получим:
, то по формуле (1) получим: .
. , то приближенное значение корня получено с достаточно большой точностью.
, то приближенное значение корня получено с достаточно большой точностью. указанным выше способом.
указанным выше способом. .
. .
. .
. . Отсюда следует, что найденное по формуле (1) приближенное значение корня будет тем точнее, чем меньше число
. Отсюда следует, что найденное по формуле (1) приближенное значение корня будет тем точнее, чем меньше число 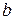 по сравнению с числом
по сравнению с числом 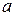 .
.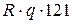 вместо нашего современного обозначения
вместо нашего современного обозначения  . В 1637 г. французский математик Р. Декарт в своей «Геометрии» использовал современный знак корня
. В 1637 г. французский математик Р. Декарт в своей «Геометрии» использовал современный знак корня 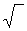 , но запись подкоренного выражения отличалась от современной. И.Ньютон в «Универсальной арифметике» (1685 г.) применял обозначение радикала еще более близкое к современному. Впервые запись корня, совпадающая с ныне принятой, встречается в «Трактате по алгебре» (1690 г.) французского математика М. Роля (1652 – 1719). Современный знак корня окончательно вошел во всеобщее применение лишь в начале XVIII в.
, но запись подкоренного выражения отличалась от современной. И.Ньютон в «Универсальной арифметике» (1685 г.) применял обозначение радикала еще более близкое к современному. Впервые запись корня, совпадающая с ныне принятой, встречается в «Трактате по алгебре» (1690 г.) французского математика М. Роля (1652 – 1719). Современный знак корня окончательно вошел во всеобщее применение лишь в начале XVIII в.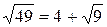 ;
;  ;
;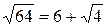 ;
;  ;
; ;
;  .
. ;
; ;
; ;
; ;
; .
. ?
? ».
». .
. ;
; ;
;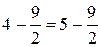 ;
; ;
; .
. .
.