
|
|
Не существует рационального числа, квадрат которого равен. 2.
Можно доказать, что не существует рационального числа, квадрат которого равен 3, 5, 7, 10 Представление рационального числа в виде бесконечной десятичной периодической дроби. Напомним основные правила. Правила обращения периодической десятичной дроби в обыкновенную дробь. Не существует правил действий над периодическими дробями. Поэтому их обращают в обыкновенные дроби по следующим правилам. Правило 1. Правильная чистая периодическая дробь равна обыкновенной, числителем которой является период периодической дроби, а знаменатель состоит из стольких девяток, сколько цифр в периоде. Например: Правило 2. Правильная смешанная периодическая дробь равна обыкновенной, в числителе которой находится разность числа, стоящего до второго периода, и числа, стоящего до первого периода, а в знаменателе столько девяток, сколько цифр в периоде, и столько нулей, сколько цифр между запятой и первым периодом. Например:
Пример 1. Вычислить:
Решение. 1) 2) 3)
4)
Ответ: Практическая часть Задание 1. Продумайте ответы на следующие вопросы: 1. Какие числа составляют множество всех рациональных чисел? Как обозначается это множество? Приведите примеры рациональных чисел. 2. Существует ли взаимно однозначное соответствие между множеством всех рациональных чисел и множеством всех точек на координатной прямой? 3. Всегда ли выполнимы действия сложения, умножения, вычитания и деления на множестве Q? 4. Что называется арифметическим квадратным корнем? Сколько существует арифметических квадратных корней из неотрицательного рационального числа а? 5. Всегда ли имеет уравнение 6. Могут ли быть равными: а) квадраты неравных чисел; б) арифметические квадратные корни из неравных чисел? 7. Назовите два рациональных числа, расположенных между числами – 0,13427 и 0. Задание 2. Возьмите чистый лист бумаги и на нем запишите ответы ко в сем устным упражнениям, приведенным ниже. Свои ответы сверьте с ответами или краткими указаниями, помещенными в конце учебного элемента в рубрике «Ваш помощник». Устные упражнения 1. Представьте в виде отношения целого числа к натуральному следующие числа: а) 1; б) 0,4; в) –1; г) –17; д) 0. 2.Какие из чисел –80; –12,5; –2; –; 0; 6; 17; 20являются: а) натуральными; б) целыми; в) рациональными, но не натуральными; г) рациональными, но не целыми ? 3.Верно ли, что: а) –4 Î N; –4 Î Z; –4 Î Q; б) 3,6 Î N; 3,6 Î Z; 3,6 Î Q; в) 14 Î N; 14 Î Z; 14 Î Q. 4.Пусть х Î Q, у Î Q. Какому из числовых множеств принадлежит х + у; х – у; ху; ? 5.Укажите два таких рациональных числа, чтобы их сумма, произведение, частное были равны между собой. 6.Укажите несколько рациональных чисел, заключенных между: а) 6 и 6,1; б) –0,02 и 0; в) –201 и –200; г) и . 7.Укажите такие рациональные числа k и q, при которых имеет место соотношение: а) = 0; в) = –1; д) < 1; б) = 1; г) > 1; е) · > 1. 8.Могут ли два взаимно обратных числа иметь противоположные знаки ? 9. Вычислите: + + + … + + . 10. Решите уравнение: а) х2 = 25; б) х2 = 2; в) х2 = 3. 11.Докажите, что верно равенство: а) = 11; б) = 20; в) = 0,5; г) = 0,3. 12.Какие из данных выражений имеют смысл: а) , , –; б) , , –, –. 13.Найдите значение корня: а) ; г) ; ж) ; б) ; д) ; з) ; в) ; е) ; и) . 14.Почему уравнение не имеет корней: а) = –3; в) –= 3; б) + 2 = 0; г) 3= –12 ? 15.Докажите, что а) число 7 есть арифметический квадратный корень из 49; б) число 0,5 есть арифметический квадратный корень из 0,25; в) число –1,3 не является арифметическим квадратным корнем из 1,69. 16.Докажите, что: а) = 9; в) = 4,1; б) = 2,2; г) = 0,18. 17.Вычислите арифметический квадратный корень из числа: а) 25; б) 121; в) 0,36; г) 2,56; д) ; е) 6. 18.Найдите значение корня: а) ; в) ; д) ; ж) ; б) ; г) ; е) ; з) .
19. Даны дроби а) ; б) ; в) ; г) . Не пользуясь алгоритмом деления, выясните, какие из обыкновенных дробей обращаются в конечные десятичные дроби. 20.Представьте в виде бесконечной десятичной дроби рациональное число: ; ; ; . 21.Каково наименьшее рациональное число, большее числа 5,7 в бесконечную запись которого не входят цифры 0, 1, 2, 3 ? 22.Записать рациональное число в виде периодический дроби: ; ; . 23.Представьте в виде обыкновенной дроби: 0,(4); 0,(5); 0,(21); 1,(137).
Задание 3. Докажите, что если a и b – рациональные числа и Задание 4. Докажите, что между любыми двумя рациональными числами содержится бесконечное множество рациональных чисел. Задание5.Укажите несколько рациональных чисел, заключенных между: а) 6 и 6,1; б) –0,01 и 0; в) –102 и –101; г) Задание 6. Найдите х из пропорции: а) б) Задание 7. Найдите х из пропорции: Задание 8. Вычислите: а) б) Задание 9. Вычислите: а) б) в) Задание 10. Вычислите: а) б) в) г) д) Задание 11. Вычислите: а) б) Задание 12.Найдите число, 7,5 % которого равно А, где Рубрика “Ваш помошник” К заданию 2. Ответы к устным упражнениям. 1. а) ; б) ; в) –; г) –; д) , где n Î N. 2. а) 6; 17; б) –80; –2; 0; 6; 17; в) –80; –12,5; –2; –; 0; 20; г) –12,5; –; 20. 3. а) неверно; верно; верно; б) неверно; неверно; верно; в) верно; верно; верно. 4. Множеству рациональных чисел. 5. и –1, так как + (–1) = × (–1) = : (–1) = –. 6. Например: а) 6,01; 6,02; 6,03; б) –0,01; –0,001; –0,005; в) –200,5; –200,4; – 200,3; г) 0,3; 0,32; 0,38. 7. а) k = 0, q – любое рациональное число, отличное от 0; б) k = q, q ¹ 0; в) k = –q, q ¹ 0; г) k > q > 0 либо k < q < 0; д) 0 < k < q либо q < k < 0; е) таких рациональных чисел k и q не существует. 8. Нет. 9. 1 – = 0,9. 10. а) –5; 5; б) –2; 2; в) –; . 11. Докательство: а) 11 > 0 и 112 = 121, следовательно, = 11; 12. а) Да; нет; да; б) да; нет; да; да. 13. а) 5; б) 7; в) 100; г) 0,9; д) 0,4; е) 0,2; ж) ; з) 1; и) 1.
16. а) 9 > 0 и 92 = 81. 17. а) 5; б) 11; в) 0,6; г) 1,6; д) ; е) . 18. а) 10; б) 40; в) ; г) ; д) 0,9; е) ; ж) 0,1; з) 0,001. 19. а) 70 = 2 × 5 × 7, не обращается; б) 26 = 2 × 13, не обращается; в) 16 = 2 × 2 × 2 × 2, обращается; г) 50 = 2 × 52, обращается. 20. = 0,5000…; = 0,25000…; = 0,125000…; = 0,2333… . 21. 5,74444… 22. = 0,(2); = 0,(6); = 0,1(6). 23. 0,(4) = ; 0,(5) = ; 0,(21) = ; 1,(137) = . К заданию 6. а) 8,64; б) 13; в) К заданию 7. 9. К заданию 8. а) К заданию 10.а) 25; б) 0,01; в) 0,12; г) 21 д) 0,001024 К заданию 11. а) 12; б) 9. К заданию 12. 200. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ;
;  .
. ;
; .
. .
. ;
; ;
; ;
;
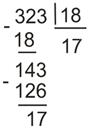
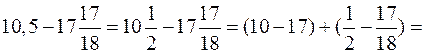
 .
. .
. рациональные корни при a > 0, a = 0, a < 0 и, если имеет, то сколько?
рациональные корни при a > 0, a = 0, a < 0 и, если имеет, то сколько?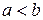 , то число
, то число 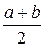 лежит между ними.
лежит между ними. и
и  .
. ; в)
; в)  ;
; ; г)
; г)  .
. .
. ;
; .
. ;
; ;
; .
. ;
; ;
; ;
; ;
; .
. ;
; .
. .
. ; г) 9.
; г) 9. ; б)
; б)  .
.