
|
|
УЭ-9. Метод промежутков при решении неравенств, содержащих переменную под знаком модуляВаша цель: уяснить сущность метода промежутков и уметь применять его к решению неравенств, содержащих переменную под знаком модуля. Входная информация
Сущность метода промежутков. Чтобы решить, например, неравенство
1) Находят область допустимых значений неравенства; 2) находят нули подмодульных выражений; 3) разбивают область допустимых значений нулями подмодульных выражений на промежутки; 4) на каждом из полученных промежутков неравенство записывают без знака модуля и решают с учетом знака неравенства, задающего этот промежуток; Найденные множества решений объединяют и записывают ответ.
Учимся решать неравенства с модулем методом промежутков.Ознакомьтесь с примерами решения неравенств, содержащих переменную под знаком модуля, методом промежутков. Пример 1. Решим неравенство: |x + 2| + |x – 3| > х + 5. Решение. Нули подмодульных выражений: числа –2 и 3, они разбивают координатную прямую на три промежутка, которые можно задать неравенствами: х < –2, –2 £ x £ 3 и x > 3. Будем искать решения неравенства на каждом из промежутков. 1) Û Û (x < –2). 2) Û Û (–2 £ x 0). 3) Û Û (x > 6).
Находим объединение полученных решений и записываем ответ. Ответ: (–¥; 0) U (6; +¥). Практическая часть Задание 1.Решите неравенство: а) |х – 3| ³ 2х + 1; в) |х – 2| < ; б) |3х + 1| ³ 7х – 5; г) |х – 1| < . Задание 2. Решите неравенство: а) 2 |х + 1| > х + 4; в) 4 |х + 2| < 2х + 10; б) 3 |х – 1| £ х + 3; г) 3 |х + 1| ³ х + 5. Задание 3. Решите неравенство: а) |х – 2| + |х + 3| > 5; б) |2х + 5| – |3х – 4| £2х – 4; в) |5 – 2х| + |3х – 4| ³ 2х + 3; г) |х – 1| + 2 |2х + 3| – |2 – х| > 5 + |х|. Задание 4. Решите неравенство |х + 1| + |х – 4| > 7, указав наименьшее целое положительноех, удовлетворяющее этому неравенству. УЭ-10. Решение неравенств вида ( вместо знака Ваша цель: научиться решать неравенства данного вида Входная информация Метод промежутков является наиболее универсальным способом решения неравенств. Однако в некоторых случаях целесообразно использовать другие методы.
Метод равносильных переходов. Используют равносильные переходы, позволяющие избавиться от знака модуля. Приведем некоторые из них, применяемые при решении простейших неравенств, содержащих переменную под знаком модуля.
1. Если 2. Если Учимся решать неравенства различными способами.
Пример 1. Решим неравенство: |x – 1| < 3. Решение. 1-й способ. Поскольку |x – 1| можно рассматривать как расстояние на координатной прямой между точками х и 1, то по условию задачи нужно указать на координатной прямой все точки х, которые удалены от точки 1 меньше чем на 3 единицы (рис.8 ). Отсюда находим множество решений неравенства: (–2; 4). 2-й способ. Поскольку |x – 1| = то заданное неравенство равносильно совокупности двух систем неравенств: Или Из первой системы получаем, что 1 £ х < 4, а из второй – что –2<x<1. Объединив промежутки (–2; 1) и [1; 4), получаем (–2; 4) – решение заданного неравенства. 3-й способ. Данное неравенство |x – 1| < 3 равносильно двойному неравенству –3 < x – 1 < 3, т.е. –2 < x < 4. Ответ: (–2; 4).
1. Если 2. 3. Если
1. Если 2. Множество решений неравенства 3. Если
1. Если 2. Если
Рассмотрим некоторые из них на примере решения неравенств вида Пример 2. Решить неравенство |2x + 5| ³ 6. Решение. 1-й способ. Разделив обе части данного неравенства на положительное число 2, получим равносильное неравенство |2x + 2,5| ³ 3. Задачу можно переформулировать так: на координатной прямой найти все такие точки х, которые удалены от точки –2,5 на расстояние, большее или равное 3 (рис. 9.29). Получаем: x £ –5,5 либо х ³ 0,5, т.е. объединение числовых промежутков (–¥; –5,5] и [0,5; +¥) является решением данного неравенства. 2-й способ. Данное неравенство равносильно совокупности неравенств
Выполнив равносильные преобразования, получим: х ³ 0,5 либо x £ –5,5. Объединив решения полученных неравенств, получим ответ. Ответ: (–¥; –5,5] U [0,5; +¥). Задание. Решите неравенство |2x + 5| ³ 6 третьим способом, основанным на раскрытии знака модуля.
Практическая часть Задание 1. Возьмите чистый лист бумаги и на нем запишите ответы ко в сем устным упражнениям, приведенным ниже. Свои ответы сверьте с ответами или краткими указаниями, помещенными в конце учебного элемента в рубрике «Ваш помощник».
Устные упражнения 1. Решите неравенство: а) ïхï > 2; г) ïхï £ –2; ж) ïхï ³ 0; б) ïхï ³ 2; д) ïхï > –2; з) ³ 0; в) ïхï £ 2; е) ïхï > 0; и) > –3. 2.Верно ли, что неравенство ïаï < 3 равносильно неравенствам: а) а < –3 или а > 3; в) 0 < а < 3; б) –3 < а < 3; г) а < 3 ? 3.Укажите множество решений неравенства: а) ï4хï > 16; в) ïх – 4ï > –3; б) ï4хï £ 9; г) ïх – 1ï > 0. 4.При каких значениях а) £ ; в) |х–1| > 0; б) > ; г) |х|–1 < 0? 5.Укажите множество решений неравенства: а) 1 < ïхï < 2; б) 3 < ïхï £ 5. 6.Имеет ли решение неравенство 1 < ïхï < –7 ? 7. Известно, что: а) неравенство Б) решением неравенства С некоторыми видами следующих заданий вы могли встречаться на уроках математики. Самоопределитесь, какие из следующих заданий вам необходимо выполнить. В случае затруднений обращайтесь к рубрике «Ваш помощник», за консультацией к учителю или за помощью к товарищу. Задание 2. Используя координатную прямую, решите уравнение или неравенство: а) б) в) Задание 3. Решите неравенство: а) б) Задание 4. Решите неравенство: а) б) Задание 5, подберите числа Задание 6. Решите систему неравенств: а) Задание 7. Решите неравенство: а) Задание 8. При каких значениях x значения дроби а) Задание 9. Решите неравенство: а) Задание 10. Найдите множество решений неравенства Задание 11. Найдите сумму всех целых решений неравенства Задание 12. Решите неравенство: а) б) в)
Рубрика “Ваш помощник” К заданию 1. Ответы на устные упражнения 1. а) (–¥; –2) U (2; +¥); е) (–¥; 0) U (0; +¥); б) (–¥; –2] U [2; +¥); ж) R; в) [–2; 2]; з) R; г) нет решений; и) R. д) R; 2. а) неверно; б) верно; в) неверно; г) неверно.
3. а) (–¥; –4) U (4; +¥); б) [–; ]; в) R; г) (–¥; 1) U (1; +¥). 4. а) (–¥; –2] U [2; +¥); б) (–2; 2); в) (–¥; 0) U (0; +¥); г) х < 0. 5. а) (–2; –1) U (1; 2); б) [–5; 3) U (3; 5]. 6. Не имеет. К заданию 3. а) К заданию 4. а) г) К заданию 5. а)
УЭ-14. Решение неравенств вида ( вместо знака Ваша цель: научиться решать неравенства вида Входная информация. Решение неравенств вида
1. 2. 3.
Решение неравенств вида
1. 2.
Решение неравенств вида
Учимся решать неравенства с модулем. Ознакомьтесь с решением некоторых неравенств с модулем. Пример. Решим неравенство: |х – 4| < |x – 2|. Решение. В силу свойства модуля |а| < |b| имеет место тогда и только тогда, когда а2 < b2 имеем: (|x – 4| < |x – 2|) Û ((x – 4)2 < (x – 2)2) Û ((x – 4)2 – (x – 2)2 < 0) Û Û (–2(2x – 6) < 0) Û (x – 3 > 0) Û (x > 3). Заметим, что неравенство |ах + b| < |сх + d| равносильно неравенству (ах + b)2 < (сх + d)2. Практическая часть Задание 1. Возьмите чистый лист бумаги и на нем запишите ответы ко в сем устным упражнениям, приведенным ниже. Свои ответы сверьте с ответами или краткими указаниями, помещенными в конце учебного элемента в рубрике «Ваш помощник». 1. Найдите множество решений неравенства: а) д)
2. Решите неравенство: а) д) С некоторыми видами следующих заданий вы могли встречаться на уроках математики. Самоопределитесь, какие из следующих заданий вам необходимо выполнить. В случае затруднений обращайтесь к рубрике «Ваш помощник», за консультацией к учителю или за помощью к товарищу. Задание 2. Решите неравенство: а) |х – 3| ³ 2х + 1; в) |х – 2| < ; б) |3х + 1| ³ 7х – 5; г) |х – 1| < . Задание 3.Решите неравенство: а) 2 |х + 1| > х + 4; в) 4 |х + 2| < 2х + 10; б) 3 |х – 1| £ х + 3; г) 3 |х + 1| ³ х + 5. Задание 4. Решите неравенство: а) |х – 1| > |х + 3|; в) |х| > |2 – х|; б) |х – 3| > |х – 5|; г) |х – 5| ³ |х|. Задание 5. Решите неравенство: а) Рубрика “Ваш помощник” К заданию 1. Ответы на устные упражнения 1. а){-3;3}; д) (-
б) (- в) (- г) (- 2. а) (- б) нет решений; е) [0;+ в) (- г) нет решений; з) (- К заданию 2. а) К заданию 3. а) К заданию 4. а) К заданию 5. а)

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 :
: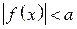
 < может стоять любой из знаков
< может стоять любой из знаков 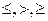 ).
).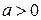 , то
, то 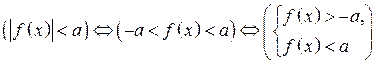 .
. , то неравенство
, то неравенство 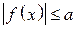
 .
.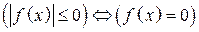 .
. , то неравенство
, то неравенство 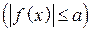 решений не имеет.
решений не имеет.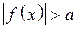
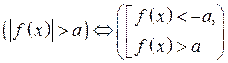 .
.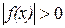 совпадает с областью определения выражения
совпадает с областью определения выражения 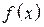 , из которой исключены корни уравнения
, из которой исключены корни уравнения 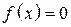 .
.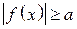
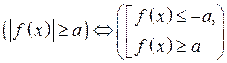 .
.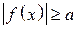 совпадает с областью определения выражения
совпадает с областью определения выражения  вернонеравенство:
вернонеравенство: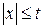 имеет единственное решение. Чему равно
имеет единственное решение. Чему равно  ?
?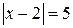 ;г)
;г) 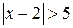 ;ж)
;ж)  ;
;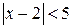 ; д)
; д) 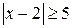 з)
з)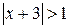 ;
;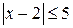 ; е)
; е)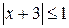 ;и)
;и)  .
.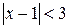 ; в)
; в)  ; д)
; д) 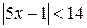 ;
;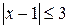 ; г)
; г) 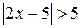 ; е)
; е) 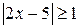 .
.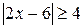 ; в)
; в) 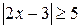 ; д)
; д) 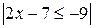 4
4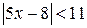 ; г)
; г) 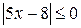 ; е)
; е) 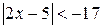 .
.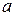 и
и 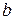 так, чтобы множеством решений неравенства
так, чтобы множеством решений неравенства  был числовой отрезок: а)
был числовой отрезок: а)  ; б)
; б) 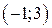 .
.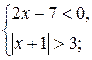 б)
б) 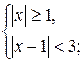 в)
в) 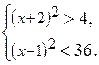
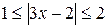 ; б)
; б) 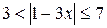 .
.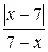 отрицательны? б)
отрицательны? б)  не больше нуля?
не больше нуля? ; б)
; б) 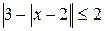 .
.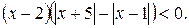
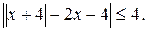
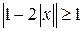 ; г)
; г) 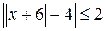 ;
;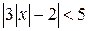 ; д)
; д)  ;
;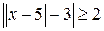 ; е)
; е)  .
. ; б)
; б) 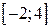 ; в)
; в)  ; г)
; г) 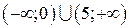 ; д)
; д) 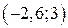 ; е)
; е) 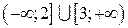 .
.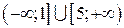 ; б)
; б)  ; в)
; в) 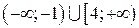 ;
; ; д) нет решений; е)
; д) нет решений; е)  .
.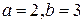 ,т.е.
,т.е. 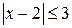
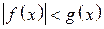
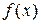 и
и 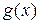 выражения вида
выражения вида 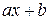 и вместо знака < может стоять любой из знаков
и вместо знака < может стоять любой из знаков 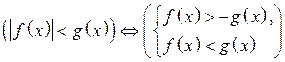 .
.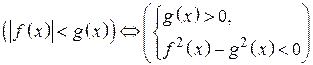 .
.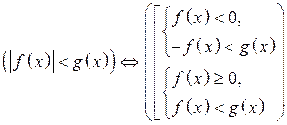 .
.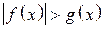 , где
, где 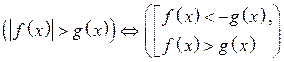 .
.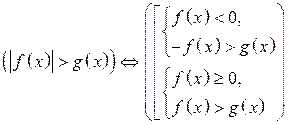 .
.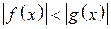 , где
, где 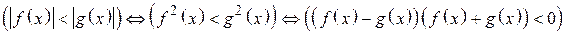 .
.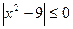 ; б)
; б)  ; в)
; в) 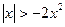 ; г)
; г) 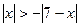 ;
;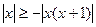 ; е)
; е) 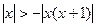 ; ж)
; ж) 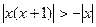 ; з)
; з)  .
. ; б)
; б) 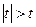 ; в)
; в) 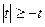 ; г)
; г)  ;
; ; е)
; е)  ; ж)
; ж) 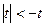 ; з)
; з) 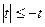 .
.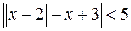 ; б)
; б) 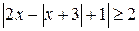 .
. ;+
;+ 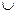 (0;+
(0;+ 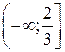 ; б)
; б) 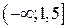 ; в)
; в)  ; г)
; г)  .
.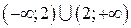 ; б)
; б) 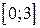 ; в)
; в)  ; г)
; г)  .
.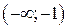 ; б)
; б) 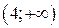 ; в)
; в) 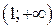 ; г)
; г) 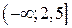 .
.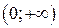 ; б)
; б) 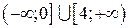 .
.