
|
|
УЭ 4 . Решение задач с помощью квадратных уравненийВаша цель: закрепить умения и навыки по решению текстовых задач с помощью уравнений. Входная информация Вы уже знакомы с решением текстовых задач с помощью линейных уравнений. Теперь рассмотрим решения текстовых задач с помощью квадратных уравнений. Квадратные уравнения позволяют решать многие задачи физики, химии, техники. В ходе решения текстовых задач можно проследить схему применения аппарата математики к изучению действительности. Она состоит из трех этапов. 1-й этап. Перевод реальной ситуации на математический язык (составление уравнения). 2-й этап. Решение задачи внутри построенной математической модели (решение уравнения). 3-й этап. Интерпретация полученного решения (сопоставление полученных решений с условием задачи). Задача 1.Из двух натуральных чисел второе больше первого в 8 раз. Найти эти числа, если их произведение равно 392. Решение. Пусть первое число х, тогда второе – 8x. По условию задачи составляем уравнение: x · 8x = 392,
Составленное уравнение имеет два корня: – 7 и 7. По условию допустимыми значениями переменной являются только натуральные числа, поэтому число –7 не является решением задачи. Значит, первое число равно 7, а второе 56. Ответ: 7 и 56. 3адача 2. Тело брошено вертикально вверх с начальной скоростью Решение. Из курса физики известно, что если не учитывать сопротивление воздуха, то высота h (м), на которой брошенное вертикально вверх тело окажется через t секунд, может быть найдена по формуле где Формулу (1) преобразуем к виду:
Применяя формулу для корней квадратного уравнения, получим:
По смыслу задачи Если Если Если
Условию задачи удовлетворяют оба найденных корня. Тело брошено с такой скоростью, что могло подняться выше, чем на h м. Поэтому оно побывало на высоте h м дважды: при движении вверх и при падении вниз. Упражнения Задание 1. Возьмите чистый лист бумаги и на нем запишите ответы ко в сем устным упражнениям, приведенным ниже. Свои ответы сверьте с ответами или краткими указаниями, помещенными в конце учебного элемента в рубрике «Ваш помощник».
1.Составьте уравнение для решения задачи: а) Одно число больше другого на 3, а их произведение равно 70. Найдите эти числа. б) Гипотенуза прямоугольного треугольника равна 10 см. Найдите катеты треугольника, если известно, что один из катетов больше другого на 2 см. 2. Составьте уравнение для решения задачи: а) Одно число больше другого на 9, а квадрат его на 279 больше квадрата другого числа. Найдите эти числа. б) В прямоугольном треугольнике один катет на 8 см меньше гипотенузы, а другой катер на 4 см меньше гипотенузы. Найдите гипотенузу. в) Найдите три последовательных натуральных числа, сумма квадратов которых равна 1589. С некоторыми видами следующих заданий вы могли встречаться на уроках математики. Самоопределитесь, какие из следующих заданий вам необходимо выполнить. В случае затруднений обращайтесь к рубрике «Ваш помощник», за консультацией к учителю или за помощью к товарищу. Задание 2. а) Произведение двух последовательных натуральных чисел равно 156. Найдите эти числа. б) Произведение двух натуральных чисел, одно из которых на 7 больше другого, равно 198. Найдите эти числа. Задание 3. Катет прямоугольного треугольника меньше гипотенузы на 8 см, другой катет равен 20 см. Найдите периметр треугольника. Задание 4. Периметр прямоугольного треугольника равен 36 см, а гипотенуза 15 см. Найдите катеты треугольника. Задание 5.. Периметр прямоугольника равен 58 см. Если одну из его сторон увеличить на 5 см, а другую – на 3 см, то площадь прямоугольника увеличится на 126 см2. Найдите стороны прямоугольника. Задание 6. Радиус одной из двух концентрических окружностей на 5 см больше радиуса другой. Площадь кольца, заключенного между этими окружностями, составляет 1,25 площади малого круга. Найдите радиусы окружностей. (Указание. Задание 7. Каждый учащийся одного класса задумал поздравить с Новым годом каждого своего одноклассника поздравительной открыткой. Оказалось при этом, что было послано 1332 открытки. Сколько было учащихся в этом классе ? Задание 8. На плоскости дано несколько точек. Никакие три из них не лежат на одной прямой. Всякие две точки соединены отрезком. Таких отрезков оказалось 190. Сколько было точек на плоскости ? Задание 9. В футбольном турнире сыграно 240 матчей, причем каждая команда играет со всеми остальными на своем и чужом полях по одному разу. Сколько футбольных команд участвовало в турнире ? Задание 10. По окончании парусной регаты все экипажи обменялись друг с другом памятными вымпелами. Сколько экипажей участвовало в состязании, если количество вымпелов оказалось равным 506 ? Задание 11. В однокруговом шахматном турнире было сыграно 105 партий. Сколько человек участвовало в соревновании ? Рубрика «Ваш помощник» К заданию 1. Ответы к устным упражнениям. 1. а) х(х – 3) = 70. Искомые числа: 10 и 7 либо –10 и –7; б) х(х + 3) = 10. Катеты треугольника: 2 5 см. Учащимся можно предложить угадать корни составленных уравнений. 2. а) х2 – (х – 9)2 = 279, где х – большее число; б) х2 = (х – 8)2 + (х – 4)2; в) n2 + (n + 1)2 + (n + 2)2 = 1589.
УЭ 5. Теорема Виета Ваша цель:знать теорему Виета для квадратного уравнения Входная информация Для квадратного уравнения
Теорема 1. Если квадратное уравнение
Теорема 1. Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а их произведение равно свободному члену. В частности, сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а их произведение равно свободному члену. Теорема 2. Если числа
В частности, если Как уже отмечалось, используя теорему, обратную теореме Виета, можно находить корни приведенного квадратного уравнения путем подбора. Если заданы корни квадратного уравнения, то можно составить и само уравнение, используя теорему, обратную теореме Виета. Рассмотрим это на примерах. Пример 1. Составим квадратное уравнение, корни которого равны: Решение. Найдем сумму и произведение корней: Пример 2. Составим квадратное уравнение, корни которого равны Решение. Найдем сумму и произведение корней: Практическая часть Задание 1. Возьмите чистый лист бумаги и на нем запишите ответы ко в сем устным упражнениям, приведенным ниже. Свои ответы сверьте с ответами или краткими указаниями, помещенными в конце учебного элемента в рубрике «Ваш помощник». Устные упражнения 1. Не решая уравнения, укажите сумму и произведения корней уравнения. Подберите корни уравнения: а) х2 – 13х + 12 = 0; в) х2 – 7х + 10 = 0; б) х2 –х – 2 = 0; г) х2 – 3х – 10 = 0. 2.Составьте приведенное квадратное уравнение, зная его корни: а) 2 и 7; б) –7 и 3; в) –10 и –30; г) 0 и 7. 3.Составьте квадратное уравнение, имеющее: а) два положительных корня; б) два отрицательных корня. 4.При каком условии по крайней мере один из корней уравнения ах2 + bх + с = 0 равен 0 ? 5.При каком значении а равенство является тождеством: а) х2 + 5х + а = (х + 2)(х + 3); б) х2 + ах + 2 = (х + 1)(х + 2) ? 6.Зная, что данное равенство является тождеством, найдите а и k: а) х2 – 9х – 22 = (х + а)(х – 2); б) 3х2 + 17х – 6 = (kх + а)(х + 6). 7.Почему квадратное уравнение с рациональными коэффициентами не может иметь один корень рациональный, а другой – иррациональный ? 8.Не решая уравнения х2 – 2х – 1 = 0, определите, является ли число 1 – его корнем. 9.Почему приведенное квадратное уравнение с иррациональными коэффициентами не может иметь двух рациональных корней ? 10.Корень квадратного уравнения с рациональными коэффициентами: а) х1 = 1 – ; б) х1 = 2 + . Укажите второй корень и соответствующее уравнение. 11. Корни какого из уравнений х2 – 7х = 0, х2 – 2х – 24 = 0, а) сумма корней равна 7, а произведение корней равно – 14; б) один из корней равен 7; в) корни равны. 12. Определите недостающие коэффициенты в следующих квадратных уравнениях: а) х2 – 6х + … = 0, если х1 = 2, х2 = …; б) х2 – …х + 18 = 0, если х1 = 3, х2 = …; в) х2 – 5х + … = 0, если х1 = –1, х2 = … . С некоторыми видами следующих заданий вы могли встречаться на уроках математики. Самоопределитесь, какие из следующих заданий вам необходимо выполнить. В случае затруднений обращайтесь к рубрике «Ваш помощник», за консультацией к учителю или за помощью к товарищу. Задание 2.Решите уравнение и выполните проверку по теореме, обратной теореме Виета: а) б) в) Задание 3. Найдите подбором корни уравнения: а) б) в) г) Задание 4. Может ли уравнение а) б) в) Задание 5.Почему квадратное уравнение с рациональными коэффициентами не может иметь один корень рациональный, а другой иррациональный ? Задание 6. Составьте квадратное уравнение, имеющее корнями следующие числа: а) 3 и 1,5; б) – 0,2 и – 0,2; в) Задание 7. Составьте квадратное уравнение с рациональными коэффициентами, один из корней которого равен: а) Задание 8. Составьте квадратное уравнение, корнями которого являются взаимно обратные числа а и Задание 9. Составьте квадратное уравнение, имеющее корень Задание 10. Составьте квадратное уравнение, корни которого были бы на 2 меньше корней уравнения Задание 11. Не решая уравнения Задание 12. Не находя корней уравнения а) б) ( Задание 13. Не решая уравнения Задание 14. Не решая уравнения Задание 15. Не решая уравнения Задание 16. Найдите все значения а, для которых квадрат разности корней уравнения Задание 17. Найдите зависимость между коэффициентами уравнения Задание 18. В каждом уравнении найдите р или q, использовав дополнительные условия: а) б) в) г) д) Задание 19. В уравнении Задание 20. При каком значении q квадрат разности корней уравнения Задание 21. Какими должны быть р и q, чтобы уравнение Задание 22. В уравнении Рубрика «Ваш помщник» 1. а) 1, 12; б) –1, 2; в) 2, 5; г) –2, 5. 2. а) х2 – 9х + 14 = 0; б) х2 + 4х – 21 = 0; в) х2 + 40х + 300 = 0; г) х2 – 7х = 0. 3. а) х2 – 3х + 2 = 0; б) х2 – 15х – 8 = 0. 4.При с = 0. 5. а) а = 6; б) а = 3. 6. а) Так как х1 = –2, то х2 = = 11. Значит, а = –х2= –11. б) так как х1 = –6, то х2 = (–2) : (–6) = . Тогда 3х2 + 17х – 6 = 3(х – )(х + 6) = (3х – 1)(х + 6), откуда k = 3, а = –1. 8. Если 1 – – корень данного уравнения, то и 1 + тоже является его корнем. Составив квадратное уравнение по его корням, будем иметь х2 – 2х – 1 = 0, что и показывает, что 10. а) х2 = 1 + ; х2 – 2х – 2 = 0; б) х2 = 2 – ; х2 – 4х – 2 = 0. 11. а) х2 – 7х – 14 = 0; б) х2 – 7х = 0; х2 – 7х – 14 = 0; в) х2 – 12х + 36 = 0. 12. а) в этом случае рассуждение может быть построено так: «Если уравнение приведенное, то сумма его корней равна второму коэффициенту, взятому с противоположным знаком; х2 – 6х + … = 0 – приведенное уравнение, следовательно, х1 + х2 = 6. Из того, что х1 + х2 = 6 и х1 = 2 следует, что б) х2 = 6; р = 9; в) х2 = 6; q = –6. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 = 392, или
= 392, или 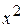 = 49, откуда
= 49, откуда  .
. (м/с). Через сколько секунд оно будет на высоте h (м) над точкой бросания ?
(м/с). Через сколько секунд оно будет на высоте h (м) над точкой бросания ?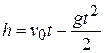 , (1)
, (1)  .
. .
. < 2gh (т. е.
< 2gh (т. е.  ), то уравнение не имеет действительных корней. Значит, начальная скорость
), то уравнение не имеет действительных корней. Значит, начальная скорость  (т. е.
(т. е.  ), то уравнение имеет единственный корень: физический смысл задачи заключается в том, что через
), то уравнение имеет единственный корень: физический смысл задачи заключается в том, что через  секунд тело достигнет высоты h один раз.
секунд тело достигнет высоты h один раз. (т. е.
(т. е.  ), то уравнение имеет два корня
), то уравнение имеет два корня 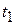 и
и  и притом оба положительных, так как
и притом оба положительных, так как и
и  .
. .)
.) и уметь применять ее для решения разнообразных задач.
и уметь применять ее для решения разнообразных задач. и
и  , то их сумма равна
, то их сумма равна  , а произведение равно
, а произведение равно  .
. , то числа
, то числа  и
и  являются корнями приведенного квадратного уравнения
являются корнями приведенного квадратного уравнения  .
. .
. . Искомое уравнение:
. Искомое уравнение:  .
. .
.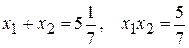 . Искомое уравнение:
. Искомое уравнение:  , или
, или  .
. ; г)
; г) 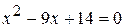 ;
; , д)
, д)  ;
; ; е)
; е)  .
. ; д)
; д)  ;
; ; e)
; e)  ;
;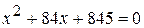 ; ж)
; ж)  ;
; ; з)
; з)  .
. ;
; ;
; ?
? + 2 и
+ 2 и  и
и 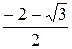 ; д)
; д)  и
и 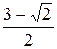 .
. ; б)
; б)  ; в)
; в)  .
.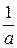 .
. .
.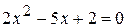 .
. , найдите: а)
, найдите: а)  ; б)
; б)  ; в)
; в) 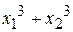 (
(  , вычислите:
, вычислите: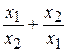 ; д)
; д)  ; е)
; е) 
 – корни исходного уравнения).
– корни исходного уравнения).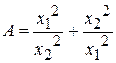 , где
, где  ; б)
; б)  , где
, где  , где
, где  равен 1.
равен 1. , если
, если  ;
; , если
, если  ;
; , если
, если  ;
; , если
, если  ;
; , если
, если  .
.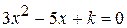 подберите значение k так, чтобы
подберите значение k так, чтобы  .
. равен 16 ?
равен 16 ? найдите k, если
найдите k, если 