
|
|
УЭ- 6. Задачи на исследование знаков корнейПриведенного квадратного уравнения Ваша цель: научиться решать задачи на исследование знаков корней приведенного квадратного уравнения. Входная информация Рассмотрим приведенное квадратное уравнение 1) Пусть q > 0; так как q= а) если р > 0, сумма б) если р < 0, сумма в) если р = 0, уравнение не имеет действительных корней 2) Пусть q < 0. В этом случае из равенства а) если р > 0, сумма б) если р < 0, сумма в) если р = 0, то 3) Пусть q = 0; так как Полученные результаты исследования знаков корней приведенного квадратного уравнения показаны в таблице.
Если обе части квадратного уравнения
которое будет иметь те же корни, что и исходное. В этомслучае , поэтому исследование знаков корней, которое выполнено ранее, будет таким же и для уравнения Пример 1. Не решая уравнение Находим дискриминант: Корни действительны и различны между собой; так как их произведение Пример 2. Не решая уравнение Корни действительны и различны между собой, так как их произведение отрицательно (корни разных знаков);
Практическая часть Задание 1. Продумайте ответы к устным упражнениям: 1. Известно, что дискриминант уравнения 2. Приведите пример квадратного уравнения, у которого: а) один корень равен нулю, а второй отличен от нуля; б) оба корня равны нулю. 3. Докажите, что уравнение 4. Докажите, что уравнение имеет два различных корня и определите знаки этих корней: а) Задание 2.Не решая уравнения, определите знаки его корней: а) б) в) г) Задание 3. Докажите, что уравнение не может иметь корни одинаковых знаков: а) Задание 4. Не решая уравнения, выясните, имеет ли оно корни, и если имеет, то определите их знаки: а) б) в) УЭ-7. Решение биквадратных уравнений Ваша цель: научиться решать биквадратные уравнения Входная информация Понятие биквадратного уравнения. Как найти корни биквадратного уравнения. Пример 1. Решим уравнение Решение. Введя подстановку
Значит, Ответ: -1 и 1. Как найти корни любого уравнения Пример 2. Решим уравнение Решение. Введя подстановку
Тогда Ответ: -2; 3. Практическая часть Задание 1. Возьмите чистый лист бумаги и на нем запишите ответы ко в сем устным упражнениям, приведенным ниже. Свои ответы сверьте с ответами или краткими указаниями, помещенными в конце учебного элемента в рубрике «Ваш помощник». Устные упражнения 1. Решите уравнение: а) х4 – 5х2 = 0; б) х4 + 6х2 = 0; в) 7х4 = 0; г) х4 + 3х2 + 1 = 0. 1. а) 0; ; б) 0; в) 0; г) Æ. 2.Сколько различных корней имеет уравнение х4 – 16 = 0 ? 2.Два корня. 3.Решите уравнение: а) х4 – х2 + 2 = 0; б) х4 – 0,09х2 = 0. 3. а) нет решений; б) 0; –0,3; 0,3. 4.Уравнение х4 + 4х2 + 5 = 0 не имеет действительных корней. Почему этот вывод можно сделать не решая уравнения ? 4. х4 ³ 0, 4х2 ³ 0 и 5 > 0. 5.Имеет ли корни биквадратное уравнение 2х4 – 5х2 + 6 = 0 ? 5. Не имеет, поскольку Д = 25 – 4 × 2 × 6 < 0. 6.Почему биквадратное уравнение, имеющее корень, равный х0, имеет второй корень, равный –х0 ? 6. Поскольку С некоторыми видами следующих заданий вы могли встречаться на уроках математики. Самоопределитесь, какие из следующих заданий вам необходимо выполнить. В случае затруднений обращайтесь к рубрике «Ваш помощник», за консультацией к учителю или за помощью к товарищу. Задание 2. Решите уравнение: а) б) в) Задание 3. Докажите, что уравнение Задание 4. Разложите на множители многочлен: а) Задание 5.Сократите дробь: а) б) Задание 6. Решите уравнения:
Найдите сумму и произведение корней каждого из данных уравнений и отметьте свойства корней биквадратных уравнений. Задание 7. Докажите, что если число α является корнем биквадратного уравнения Задание 8. Составьте биквадратное уравнение, если один из его корней равен Задание 9.Зная, что Задание 10. Докажите, что уравнение Задание 11. Решите уравнение: а) б) Рубрика «Ваш помощник» 1. а) 0; ; б) 0; в) 0; г) нет решений. 2.Два корня. 3. а) нет решений; б) 0; –0,3; 0,3. 4. х4 ³ 0, 4х2 ³ 0 и 5 > 0. 5. Не имеет, поскольку Д = 25 – 4 × 2 × 6 < 0. 6. Поскольку 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 и будем считать, что его дискриминант неотрицателен. Тогда возможны следующие случаи.
и будем считать, что его дискриминант неотрицателен. Тогда возможны следующие случаи. , то оба корня имеют одинаковые знаки:
, то оба корня имеют одинаковые знаки: отрицательна
отрицательна  , значит, оба корня отрицательны;
, значит, оба корня отрицательны; , значит, оба корня положительны;
, значит, оба корня положительны; и
и  .
. следует, что корни имеют противоположные знаки:
следует, что корни имеют противоположные знаки: .
.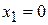 , тогда
, тогда 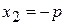 и
и  , то
, то  . Если же и р = 0, то уравнение имеет два равных корня
. Если же и р = 0, то уравнение имеет два равных корня 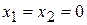


 (а ≠ 0) разделить на а, то получим приведенное квадратное уравнение
(а ≠ 0) разделить на а, то получим приведенное квадратное уравнение ,
,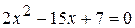 , определим знаки его корней.
, определим знаки его корней. , D > 0.
, D > 0.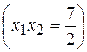 и сумма
и сумма  положительны, то оба корня положительны.
положительны, то оба корня положительны.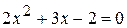 , определим знаки его корней.
, определим знаки его корней.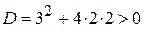 .
. отрицательный корень по модулю больше положительного.
отрицательный корень по модулю больше положительного. положителен. При каком условии корни данного уравнения будут иметь одинаковые знаки?
положителен. При каком условии корни данного уравнения будут иметь одинаковые знаки? не может иметь корни одного знака.
не может иметь корни одного знака. ; б)
; б) 
 ; д)
; д)  ;
; ; е)
; е)  ;
;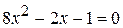 ;ж)
;ж)  ;
; ; з)
; з) 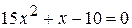 .
. ; б)
; б)  .
.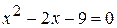 ; г)
; г)  ;
; ; д)
; д)  ;
; ; е)
; е)  .
. .
. , получим уравнение:
, получим уравнение:  . Его дискриминант
. Его дискриминант  , D > 0. Следовательно,
, D > 0. Следовательно, .
. . Так как y ≥ 0, то получим одно уравнение:
. Так как y ≥ 0, то получим одно уравнение:  . Откуда
. Откуда  .
. .Данное уравнение подстановкой
.Данное уравнение подстановкой  сводится к решению квадратного уравнения.
сводится к решению квадратного уравнения. .
. , получим уравнение:
, получим уравнение: .
. , D > 0.
, D > 0.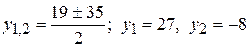 . Отсюда
. Отсюда  или
или  . Решая полученные уравнения, находим:
. Решая полученные уравнения, находим:  .
. = а(–х0)4 + b(–х0)2 + с для любого х0.
= а(–х0)4 + b(–х0)2 + с для любого х0.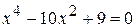 ; г)
; г) 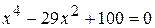 ;
;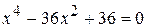 ; д)
; д)  ;
; ; е)
; е)  .
. не имеет действительных корней.
не имеет действительных корней. ; б)
; б)  ; в)
; в)  ;
; ; г)
; г) 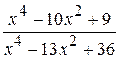 .
.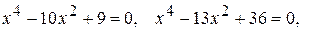
 .
. , то корнем этого уравнения также является число – α.
, то корнем этого уравнения также является число – α. , а другой
, а другой  .
. и
и  –корни уравнения
–корни уравнения 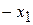 .,
.,  ,
, 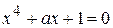 не имеет рациональных корней, если а – целое число и а ≠ 2 .
не имеет рациональных корней, если а – целое число и а ≠ 2 . ;
; .
.