
|
|
УЭ-7. Системы и совокупности линейных неравенствВаша цель:знать определение решения системы (совокупности) неравенств и знаки, применяемые для их обозначения; уметь решать системы и совокупности простейших неравенств; уметь решать двойные неравенства. Входная информация Понятие системы неравенств. Несколько неравенств с одной переменной образуют систему, если нужно найти множество всех общих решений заданных неравенств. Неравенства, образующие систему, объединяются фигурной скобкой, например:
Определение.Решением системы неравенств с одной переменной называется значение переменной, при котором каждое из неравенств системы обращается в верное числовое неравенство. Множество решений системы есть пересечение множеств решений, входящих в нее неравенств. Учимся решать системы неравенств. Рассмотрим примеры решения систем неравенств.
Пример 1. Решим систему неравенств
Решение. Преобразовав каждое неравенство, входящее в систему, получим:
Множество решений первого неравенства (–¥; 7), второго – (3; +¥). Очевидно, что множеством решений системы является пересечение этих двух множеств. Это пересечение можно найти с помощью координатной прямой . Системе неравенств удовлетворяет любое число из интервала (3; 7). Ответ: (3; 7).
Пример 2. Решим двойное неравенство –1 < < 1. Решение. Двойное неравенство можно рассматривать как систему неравенств:
Решим ее:
Множество решений системы, а следовательно, и двойного неравенства – числовой интервал (– 1; 2) (рис.2 ). Решение двойного неравенства можно найти по-другому: –1 < < 1. Умножив неравенство почленно на 3, получим: –3 < 2x – 1 < 3. Прибавляя к каждой из частей неравенства 1, получаем равносильное исходному неравенство –2 < 2х < 4. Разделив полученное неравенство почленно на 2, приходим к неравенству –1 < x < 2. Ответ: (–1; 2). Понятие совокупности неравенств. Несколько неравенств с одной переменной образуют совокупность, если нужно найти все такие значения переменной, каждое из которых является решением хотя бы одного из данных неравенств. Для обозначения совокупности неравенств используется прямая скобка [. Так, запись означает, что неравенства образуют совокупность. Иногда неравенства, образующие совокупность, записывают в строчку и отделяют друг от друга логической связкой «или». Например, 2х – 3 < 1 или 3х + 1 > 10. Значение переменной, при котором хотя бы одно из неравенств, образующих совокупность, обращается в верное числовое неравенство, называется решением совокупности неравенств. Множество решений совокупности есть объединение множеств решений входящих в нее неравенств. Учимся решать совокупности неравенств. Определим, что значит решить совокупность систем неравенств. Решить совокупность систем неравенств с переменной х – значит найти все такие значения х, которые удовлетворяют по крайней мере одной из заданных систем. Другими словами, решением совокупности систем является объединение решений этих систем. Рассмотрим примеры решения совокупностей неравенств.
Пример 4. Решим совокупность неравенств
Получаем:
Множество решений неравенства х > 9 – числовой промежуток (9; +¥), неравенства х > 4 – числовой промежуток (4; +¥). Пользуясь координатной прямой, находим, что объединением этих множеств является числовой промежуток (4; ¥) (рис. 3).
Ответ: (4; +¥). Практическая часть Задание 1. Возьмите чистый лист бумаги и на нем запишите ответы на все устные упражнения приведенные ниже. Затем свои ответы сверьте с ответами или краткими указания, помещенными в конце этого учебного элемента в рубрике «Ваш помощник». Устные упражнения 1. Является ли число а) б) 2. Решите систему неравенств: а) б) в) г) д) е) 3. Решите двойное неравенство: а) б) в) 4. Решите неравенство: а) б) в) г) 5. Является ли число а) б) 6. Решите совокупность неравенств: а) б) 7. Найдите множество решений: а) б) в) г) 8. Установите соответствие между системами неравенств и множеством их решений: луч, открытый луч, полуинтервал, отрезок: а) б) в) г) 9. Объясните, почему данная система неравенств не имеет решений: а) б) в) г)
С некоторыми видами из следующих заданий вы могли встречаться на уроках математики. Самоопределитесь, какие из заданий вам необходимо выполнить. В случае трудностей обращайтесь к рубрике «Ваш помощник», за консультацией к учителю или за помощью к товарищу Задание 2. Решите систему неравенств:
а) в)
б) г) Задание 3. Придумайте систему двух линейных неравенств, имеющую множество решений: а) (–2; 4); б) (3; +¥); в) (–¥; –1); г) пустое множество. Задание 4. Решите систему неравенств: а) г)
б) д)
в) е) Задание 5.Решите двойное неравенство: а) 3 £ 2x £ 8; г) 0 £ £ 4; б) –2x < y – 5 < 2; д) –2 £ . в) 3х – 2 < 4х + 1 < 3х + 5; Задание 5. Решить систему неравенств:
а)
б)
в)
г) Задание 6.Укажите наибольшее и наименьшее целые числа, являющиеся решением системы: а) б)
Задание 7. Решите двойное неравенство а) б) в) г) Задание 8. При каких действительных Задание 9. Докажите неравенство Задание 10. Решите совокупность неравенств: а) в)
б) г)
Задание 11. Решите неравенство: а) x(x – 3) > 0; в) (2x – 1)(x + 1) > 0; б) (x – 1)(x – 2) < 0; г) x2 – 9 > 0.
Задание 12. Решите совокупность систем неравенств:
а) или
б) или
Задание 13. Решите неравенство: а) б) в) г) д) е) Задание 14. Найдите множество решений неравенства: а) б) в) Задание 14. В двузначном числе цифра десятков на 3 меньше цифры единиц. Найдите это число, если известно, что оно больше 21, но меньше 60. Задание 15. Если к некоторому натуральному числу прибавить его четверть, то Задание 16. Длина основания равнобедренного треугольника равна 14 см. Каким числом может быть выражена длина боковой стороны, если известно, что периметр треугольника меньше 60 см? Задание 17. Школьник переклеивает все свои марки в новый альбом. Если он наклеит по 20 марок на один лист, то ему не хватит альбома, а если по 23 марки на лист, то, по крайней мере, один лист окажется пустым. Если школьнику подарить такой же альбом, на каждом листе которого наклеено по 21 марке, то всего у него станет 500 марок. Сколько листов в альбоме?
Рубрика «Ваш помощник» К заданию 1.Ответы к устным упражнениям: 1. а) является; б) не является. 2. а) 3. а) 4. а) 5. а) число 6. a) 7. а) Ø; б) 8. а) отрезок; б) полуинтервал; в) луч; г) открытый луч. 9. а) первое неравенство системы не имеет решений; б) число 3 является единственным решением первого неравенства системы, но не является решением второго неравенства; в) пересечение множеств решений неравенств К заданию 2. a) К заданию 3. а) К заданию 4. a) К заданию 5. а)

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
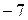 решением системы неравенств:
решением системы неравенств: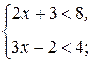
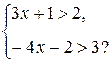
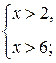
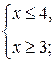
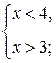
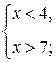
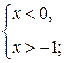
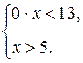
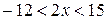 ;
; ;
;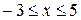 .
.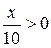 ;
;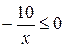 ;
;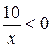 ;
;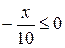 .
. решением совокупности неравенств:
решением совокупности неравенств:
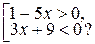
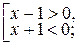
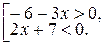
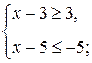
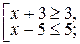
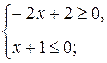
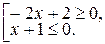
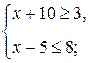
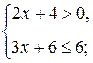
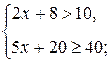
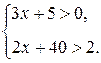
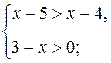
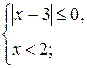
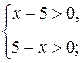
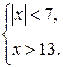
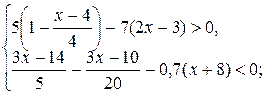
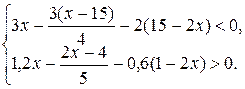
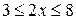 ;
; ;
;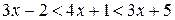 ;
;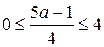 ;
;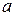 значения дроби принадлежат числовому промежутку
значения дроби принадлежат числовому промежутку  ?
?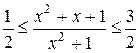 .
. ;
;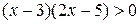 ;
;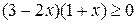 ;
; ;
;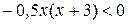 ;
;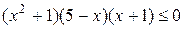 .
. ; г)
; г)  ; ж)
; ж) 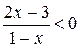 ;
;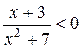 ; д)
; д) 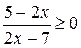 ; з)
; з)  ;
;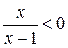 ; е)
; е) 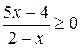 ; и)
; и)  .
.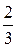 результата представляют собой число, большее 40, но меньшее 60. Найдите это число, если известно, что оно делится на 19.
результата представляют собой число, большее 40, но меньшее 60. Найдите это число, если известно, что оно делится на 19. ; б)
; б) 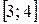 ; в)
; в)  ; г) Ø; д)
; г) Ø; д) 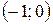 ; е)
; е) 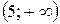 .
.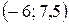 ; б)
; б) 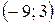 ; в)
; в) 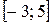 .
.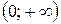 ; б)
; б)  ; г)
; г) 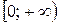 .
.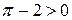 — верное числовое неравенство; б) число
— верное числовое неравенство; б) число 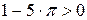 и
и  — неверные числовые неравенства.
— неверные числовые неравенства. ; б)
; б) 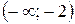 .
. ; в)
; в) 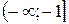 ; г)
; г) 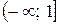 .
.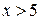 и
и 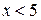 — пустое множество; г) пересечение множеств решений данной системы — пустое множество.
— пустое множество; г) пересечение множеств решений данной системы — пустое множество.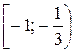 ; в)
; в) 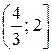 ; г) Ø.
; г) Ø.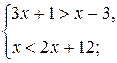 б)
б) 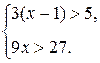
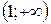 ; б)
; б)  ; в)
; в) 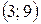 ; г) Ø; д)
; г) Ø; д) 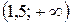 ; е)
; е) 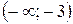 .
.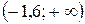 ; б) нет решений.
; б) нет решений.