
|
|
УЭ-2. Преобразование выражений,Содержащих квадратные корни Ваша цель: научиться выполнять преобразование выражений, содержащих квадратные корни. Входная информация Вынесение из-под знака корня:
Внесение под знак корня:
Учимся решать задачи. Рассмотрим некоторые задачи, связанные с понятием «арифметический квадратный корень» и некоторые способы преобразований числовых выражений, содержащих радикалы. Пример 1. Вынесем в выражении Заметим, что если предложено выполнить преобразование и не сделано оговорок о значениях переменных, то будем предполагать, что входящие в выражение переменные принимают лишь те значения, при которых оно имеет смысл. Поэтому в данном примере
Пример 2. Вынесем в выражении Данное выражение имеет смысл при любом
Задание. Обоснуйте выполнимость преобразований следующих выражений и укажите, какие значения могут принимать входящие в них переменные: а) б) в) Пример 3. Внесем в выражении Отрицательный множитель –5 нельзя представить в виде арифметического квадратного корня, и поэтому множитель –5 нельзя внести под знак корня. Однако выражение
Пример 4. В выражении Множитель если если Итак,
Задание. Обоснуйте выполнимость преобразований выражения: а) б) Практическая часть Задание 1. Возьмите чистый лист бумаги и на нем запишите ответы ко всем устным упражнениям, приведенным ниже. Свои ответы сверьте с ответами или краткими указаниями, помещенными в конце учебного элемента в рубрике «Ваш помощник». 1. При каких значениях переменной а имеет смысл выражение: ; ; 2.Сократите дробь: ; ; ; ; ; . 3.Вынесите множитель из-под знака корня: а) , x < 0; в) , x > 0, у > 0; б) , x > 0; г) , x < 0, у > 0.
4. На примере выражений 2 и –2 покажите, как можно внести множитель под знак корня.
5. При каких значениях переменной х верно равенство: а) х = ; б) (х – 1) = ?
6. На примере выражений и покажите, как можно вынести множитель из-под знака корня.
7.При каких значениях переменной верно равенство а) = 2(х – 1)2; б) = (1 – х) ?
С некоторыми видами следующих заданий вы могли встречаться на уроках математики. Самоопределитесь, какие из заданий вам необходимо выполнить. В случае трудностей обращайтесь к рубрике «Ваш помощник», за консультацией к учителю или за помощью к товарищу. Задание 2. Вынесите множитель из-под знака корня: а) б) Задание 3. Выполните действия а) Задание 4.Вынесите множитель из-под знака корня а) б) Задание 5.Вынесите множитель из-под знака корня: Задание 6.Вынесите множитель за знак корня: а) б) Задание 7.Упростите выражение: а) б) в) Задание 8. Вынесите множитель из-под знака корня а) Задание 9.Внесите множитель под знак корня: а) Задание 10. Внесите положительный множитель под знак корня: а) Задание 11.Внесите множитель под знак корня: а) б) Задание 12. Внесите множитель под знак корня: а)
Рубрика «Ваш помощник»
К заданию 1. Ответы к устным упражнениям:
1. 2. 3. а) 4. 5.а) 6. 7.а) при любом х; б) при К заданию 2.а) б) в) К заданию 3.а) УЭ-3. Действия с квадратными корнями Ваша цель: добиться того, чтобы ваши действия с квадратными корнями удовлетворяли таким требованиям, как правильность, осознанность, рациональность и прочность. Входная информация Учимся решать задачи. Пример 1. Упростим сумму
Вынесем из-под знака корня в выражении
Пример 2. Преобразуем произведение
Вынеся общий множитель (число 3) за скобки в первом множителе, получим:
Пример 3. Сократим дробь
Пользуясь равенством
С некоторыми видами следующих заданий вы могли встречаться на уроках математики. Самоопределитесь, какие из заданий вам необходимо выполнить. В случае трудностей обращайтесь к рубрике «Ваш помощник», за консультацией к учителю или за помощью к товарищу. Задание 1. Упростите выражение: а) б) в) г) д) Задание 2. Выполните действия: а) б) в) г) д) Задание 3. Упростите выражение: а) б) Задание 4.Выполните действия: а) б) в) г) Задание 5. Докажите, что значения выражений Задание 6. Упростите: а) Задание 7.Выполните деление: а) б) Задание 8. Разложите на множители: а) б) в) Задание 9. Сократите дробь: а) б) Задание 10.Упростите выражение: а) б) Задание 11.Докажите, что число а является корнем уравнения: а) б) Задание 12. Выполните действия: а) б) Задание 13.Выполните действия: а) б) в) г) д) е) Рубрика «Ваш помощник»
К заданию 1.а) К заданию 2.Обозначив данное выражение через А, получим: а) б) в)
г) д) Ответы: а) 18; б) К заданию 3. а) К заданию 4.а) К заданию 5. Имеем:
К заданию 6. а) 25; б) 21.
К заданию 7. а) 8; б) 24; в) К заданию 8. Обозначив данное выражение через А, получим: а) б) в) г) д) е) К заданию 10. а) 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , если
, если 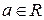 ,
,  .
. , если
, если  ,
,  .
.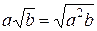 , если
, если 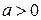 ,
,  множитель из-под знака корня.
множитель из-под знака корня. , поскольку выражение
, поскольку выражение  . Представим подкоренное выражение
. Представим подкоренное выражение 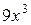 в виде произведения
в виде произведения  , в котором множитель
, в котором множитель  является степенью с четным показателем. Тогда
является степенью с четным показателем. Тогда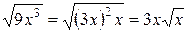 .
. множитель из-под знака корня.
множитель из-под знака корня.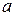 , и, поскольку
, и, поскольку  , имеем:
, имеем: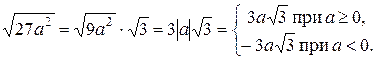
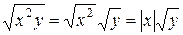 ;
; ;
; .
. множитель под знак корня.
множитель под знак корня.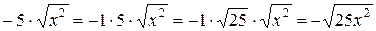 .
. внесем множитель
внесем множитель  ;
; , то
, то  .
.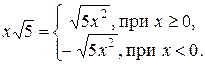
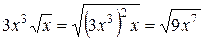 ;
; .
. ; ; ; ; ; .
; ; ; ; ; . ; в)
; в)  ; д)
; д) 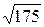 ; ж)
; ж)  ;
; ; г)
; г)  ; е)
; е) 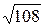 ; з)
; з)  .
. :
: ; б)
; б)  ; в)
; в)  ; г)
; г)  .
. :
: ; в)
; в)  ; д)
; д)  ; ж)
; ж)  ;
; ; г)
; г) 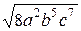 ; е)
; е)  ; з)
; з) 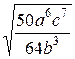 .
. .
. , если
, если 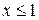 ; в)
; в)  , если
, если  ;
; , если
, если  ; г)
; г)  , если
, если  .
. , при
, при  ;
; , при
, при 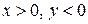 ;
;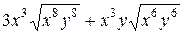 , при
, при 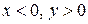 .
. :
: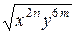 ; б)
; б)  ; в)
; в)  .
. ; б)
; б) 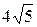 ; в)
; в)  ; г)
; г) 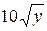 .
. ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.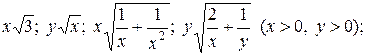
 .
. ; б)
; б)  .
.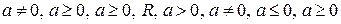 и
и  .
.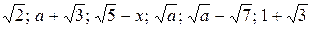 .
. ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.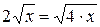 ;
;  .
.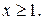
 ;
; 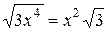 .
. ;
; ;
; .
.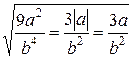 , так как
, так как  .
.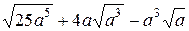 .
. множитель
множитель  , а в выражении
, а в выражении 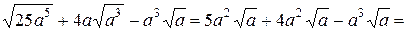
 .
.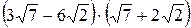 .
.
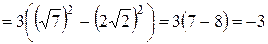 .
. .
.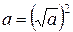 , которое выполняется при
, которое выполняется при 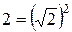 . Значит, числитель данной дроби можно представить в виде разности квадратов двух выражений:
. Значит, числитель данной дроби можно представить в виде разности квадратов двух выражений: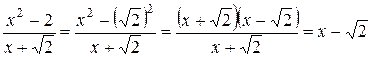 .
. ;
;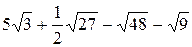 ;
; ;
; ;
; .
.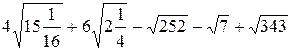 ;
; ;
; ;
; ;
; .
. , если
, если 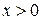 ;
; , если
, если  .
.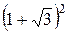 ; д)
; д)  ;
; ; е)
; е) 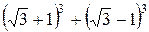 ;
; ; ж)
; ж)  ;
;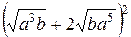 ; з)
; з)  .
. и
и 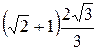 –взаимно обратные числа.
–взаимно обратные числа. ; б)
; б)  .
. ; в)
; в)  ;
; ; г)
; г)  .
. ; г)
; г)  , если
, если  ; д)
; д)  , если
, если 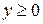 ;
;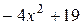 ; е)
; е)  , если
, если  ; в)
; в)  ; д)
; д)  ;
; ; г)
; г)  ; е)
; е)  .
. ;
; .
. ;
; .
. ; в)
; в)  ;
; г)
г)  .
. ;
;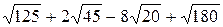 ;
;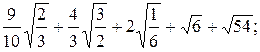
 ;
; ;
; .
. ; б)
; б) 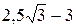 ; в)
; в)  ; г)
; г)  ; д)
; д)  .
. ;
; ;
;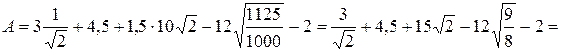
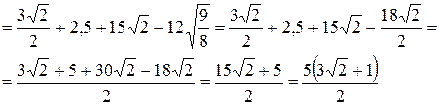
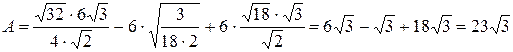 ;
; .
. ; в)
; в)  ; д) 2
; д) 2  .
.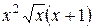 ; б)
; б) 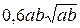 .
. ; б)
; б)  ; в)
; в)  ; д) 10; е)
; д) 10; е) 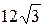 ; з)
; з) 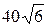 .
.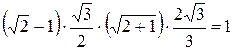 .
.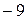 ; г) 2.
; г) 2. ;
;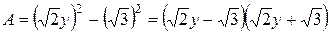 ;
; ;
; ;
; ;
; .
.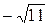 ; б)
; б) 