
|
|
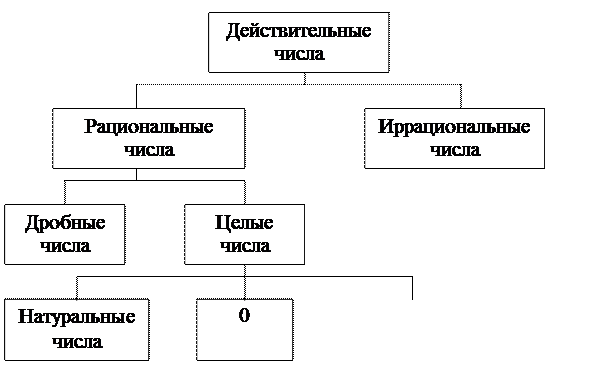
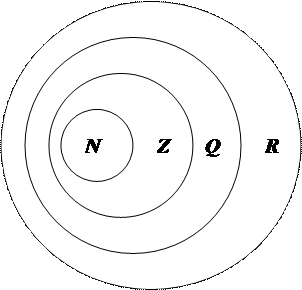
УЭ-2. Действительные числаВаша цель: углубление и расширение знаний о множестве действительных чисел. Входная информация Понятие действительного числа.Число, которое может быть представлено в виде бесконечной десятичной непериодической дроби, называется иррациональным. Примерами иррациональных чисел являются: 1) число 7,030033000333… 2) число 3,141592653689793…; 3) число 0,101001000100001…, у которого за каждой единицей идет группа нулей, содержащая на один больше, чем предыдущая группа. Множество бесконечных непериодических дробей (положительных и отрицательных) образует множество иррациональных чисел. Объединение множеств рациональных и иррациональных чисел образует множество действительных чисел. Это множество обозначают буквой R. Любое действительное число представляется в виде бесконечной десятичной дроби: Соотношения между числовыми множествами N, Z, Q и R. Оно представлено на схеме :
Разбиение множества всех действительных чисел на непересекающиеся подмножества показано на схеме 2.
 Понятие противоположных чисел. Два действительных числа называют противоположными, если их сумма равна 0. Например, – 3 и 3; Число 0 противоположно самому себе. Понятие взаимно обратных действительных чисел. Взаимно обратными числами называют два действительных числа, произведение которых равно 1. Например, Число 1 обратно самому себе. Для числа 0 обратного числа не существует. Сравнение двух действительных чисел. Число Для любых заданных действительных чисел При сравнении двух бесконечных десятичных дробей (не имеющих периода 9) пользуются следующим правилом.
если Заметим, что если целые части двух десятичных дробей разные, то та дробь больше, у которой целая часть больше. Если целые части одинаковы, то надо обратиться к наименьшему разряду, для которого цифры дробей различны: та из дробей больше, у которой цифра этого разряда больше. Действия над действительными числами. Действительные числа можно складывать, вычитать, умножать и делить. При выполнении действий в практических задачах действительные числа заменяют их приближенными значениями. Повышая точность, с которой берутся приближенные значения, получают более точное значение результата. Свойства действий над действительными числами: 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. Понятия среднего арифметического и среднего геометрического действительных чисел. Средним арифметическим нескольких чисел называют число, которое получается при делении суммы этих чисел на число слагаемых. Например, среднее арифметическое чисел 30, 70 и 95 есть число, равное числу Средним геометрическим Обобщенное неравенство Коши имеет вид:
Практическая часть Задание 1. Продумайте ответы на следующие вопросы: 1. Какие числа называются иррациональными? Приведите примеры иррациональных чисел. 2. Может ли рациональное число быть равно иррациональному? 3. Назовите: а) два иррациональных числа меньше 5; б) два отрицательных иррациональных числа; в) два иррациональных числа, расположенных между числами -2 и – 1. Задание 2. Возьмите чистый лист бумаги и на нем запишите ответы ко в сем устным упражнениям, приведенным ниже. Свои ответы сверьте с ответами или краткими указаниями, помещенными в конце учебного элемента в рубрике «Ваш помощник». 1. Укажите среди данных чисел натуральные, рациональные, иррациональные: 0,5; –6,2; ; p; ; ; 2; 9; ; ; 0,22212(221); 2,01001(0001). 2.Представьте число в виде бесконечной десятичной дроби: а) ; б) 0,(32); в) . 3.Сравните действительные числа: а) 0,(21) и 0,21; б) и 1,375; в) p и 3,1416. 4.Назовите: а) два иррациональных числа меньших 7; б) два иррациональных числа, расположенных между числами – 3 и –1. 5. Может ли рациональное число быть равным иррациональному ? 6.Назовите десятичные приближения с недостатком и с избытком с точностью до 0,01 числа: а) 14,372; б) 2,1264; в) 0,1751. 7.Какие из следующих чисел являются рациональными, какие – иррациональными: а) ; в) 0; д) 0,444…; б) ; г) –; е) 3,010010001… ? 8.Найдите множество чисел, состоящее из объединения (пересечения) множества рациональных и множества иррациональных чисел. 9. Сравните числа 0,1845 и 0,184184…; p и 3.1415. 10.В числе 0,12345678910111213…30 вычеркнуть после запятой сорок семь цифр так, чтобы полученное число было наибольшим. 11.Каким из множеств принадлежит число 0,(3); R; Z; N; Q; Q I R+; Q I R; R+; R?
12.Расположите в порядке возрастания следующие числа: 0,466; ; 0,4636363…; 0,463736; 0,4656565… . . 13.Объясните, с какой закономерностью идут цифры в бесконечной десятичной дроби: а) 5,3287177177177…; б) 0,1010010001000010…; в) 1,252255222555222255…; г) 0,410414104141410414…; д) 0,14916221364964… . 14.Не выполняя деления, скажите, конечной или бесконечной десятичной дробью можно выразить данную обыкновенную дробь: ; ; ; ; ; . 15. При каких значениях a и b верны равенства a + b = 0, a – b = 0, a · b = 0, = 0 ? 16.Представьте число в виде бесконечной десятичной дроби: а) ; в) –; д) 3; ж) 0,(66); б) ; г) ; е) 0,(5); з) 1,(37). 17. Сравните действительные числа: а) 3,5732218904 и 3,5723218904; б) 7,2537(4) и 7,253745; в) – и – . 18.Укажите число х, находящееся в интервале: а) х Î N, < х < ; б) х Î R, 1,45 < х < 1,46; в) х Î R, < х < . 19.Приведите пример двух иррациональных чисел таких, что: а) их сумма (разность) – иррациональное число; б) их сумма (разность) – рациональное число; в) их произведение (частное) – иррациональное число; г) их произведение (частное) – рациональное число. 20.Может ли: а) сумма двух рациональных чисел быть числом иррациональным; б) сумма двух иррациональных чисел быть числом рациональным ? в) сумма двух действительных чисел быть рациональным числом? 21.При каких действительных значениях х имеет место равенство х + ïхï = 0 ? Задание 3. Докажите иррациональность числа: а) Задание 4. Докажите, что числа 2,6 и 2,7 являются десятичными приближениями соответственно с недостатком и с избытком числа Задание 5. Найдите три первых десятичных знака бесконечной десятичной дроби, выражающей результат действия: а) б) Задание 6. Докажите, что сумма разность, произведение и частное двух действительных чисел, одно из которых рациональное число, отличное от нуля, а другое — иррациональное , являются иррациональными числами. Задание 7. Может ли сумма рационального и иррационального чисел быть рациональным числом ? Задание 8.Может ли сумма двух иррациональных чисел быть рациональным числом ? Задание 9.Докажите, что сумма, разность, произведение и частное двух действительных чисел, одно из которых рациональное, а другое — иррациональное, является иррациональным числом. Задение 10.Могут ли быть иррациональными числа а и b, если рациональны числа: а) а + а и а – b; в) аb и б) а – b и аb; г) а + b и Задание 11.Докажите, что сумма, разность и произведение чисел вида Задание 12.Число r— рациональное, число α – иррациональное. Рационально или иррационально число: а) Задание 13.а) Докажите, что б) Верно ли обратное утверждение ? Задание 14.Числа а, b и Задание 15.Докажите иррациональность числа: а)
Рубрика «Ваш помощник» К заданию 2. Ответы на устные вопросы: 1. Числа 2; 9 и – натуральные; числа 0,5; –6,2; ; 2; 9; ; 0,22212(221) и 2,01001(0001) – рациональные; числа ; p; ; –- иррациональные. 2. а) 0,5000…; б) 0,3232…; в) 2,6666… . 3. а) 0,(21) > 0,21; б) > 1,375; в) p < 3,1416. 4. Например: а) p, 2p; б) –, –. 5. Не может. 6. а) недост. » 14,37, изб. » 14,38; б) недост. » 2,12, изб. » 2,13; в) недост. » 0,17, изб. » 0,18. 7. а) числа ; 0; 0,444… – рациональные, а остальные – иррациональные числа. 8. Объединение – R, пересечение – Æ. 9. 0,1845 > 0,184184…; p > 3.1415 10. 0,9993. 11. R; Q, Q I R+; Q I R; R+; R. 12. 0,4636363…; 0,463736; 0,4656565…; 0,466; . 13. а) 5,328(717); б) в) 1,252255… 14. Конечные: ; ; бесконечные: ; ; ; . 15. a = –b; a = b; a = 0 или b = 0; a = 0 и b ¹ 0. 16. а) 0,666…; б) 0,6000…; в) –0,714285714; г) 0,875000…; д) 3,777…; е) 0,555…; ж) 0,6666…; з) 1,373737… . 17. а) 3,5732218904 > 3,5723218904; б) 7,2537(4) < 7,253745; в) – > – . 18. а) 2; б) 1,454; в) . 19. а) p, 2p; б) p, p (разность); p, –p (сумма); в) p, е; г) p, (произведение), p, 2p (частное). 20. а) Нет; б) да, например, + (3 – ) = 3; в) да, например, + (–) = 0. 21. При х £ 0. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , бесконечная непериодическая дробь
, бесконечная непериодическая дробь ,
,  …
…  …, где
…, где  – целое число,
– целое число,  ,
,  ,
,  , …,
, …, 
 и
и  – противоположные числа.
– противоположные числа.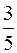 и
и  ;
;  и
и  ;
;  и
и  – взаимно обратные числа.
– взаимно обратные числа. больше числа
больше числа  , и пишут
, и пишут  – положительное число; если же разность –
– положительное число; если же разность –  .
. ,
, 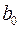 ,
, 

 …,
…, и
и  <
<  при всех
при всех  <
<  (
( 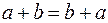 – переместительный закон сложения;
– переместительный закон сложения; – сочетательный закон сложения;
– сочетательный закон сложения; ;
; ;
; – переместительный закон умножения;
– переместительный закон умножения; – сочетательный закон умножения;
– сочетательный закон умножения; – распределительный закон умножения относительно сложения;
– распределительный закон умножения относительно сложения; ;
; , где
, где  ;
; .
. , т.е. числу 65.
, т.е. числу 65. положительных чисел
положительных чисел  .
. .
. ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д)  .
. ; в)
; в)  ; д)
; д)  ; ж)
; ж)  ;
; ; г)
; г) 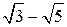 : е)
: е)  : з)
: з)  .
. ;
;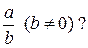
 , где a
, где a  Q и b
Q и b  б) r +
б) r + 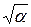
 – иррациональное число, если
– иррациональное число, если  –иррациональное число (m
–иррациональное число (m  – рациональны. Докажите, что
– рациональны. Докажите, что 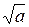 и
и  – рациональные числа.
– рациональные числа. ; б)
; б)  ; в) 1–
; в) 1–  ; г) 2 +
; г) 2 +  .
. ;
; .
.