
|
|
УЭ-5. Метод промежутков при решении уравнений, содержащих переменную под знаком модуляВаша цель: уяснить сущность метода промежутков и уметь применять его к решению уравнений, содержащих переменную под знаком модуля. Входная информация Сущность метода промежутков. Уравнения, содержащие переменную под знаком модуля, часто решают, используя метод промежутков. Сущность метода промежутков состоит в следующем: 1) находят нули подмодульных выражений; 2) разбивают координатную прямую нулями подмодульных выражений на промежутки; 3) на каждом полученном промежутке уравнение записывается без знака модуля и решается с учетом их; 4) найденные множества решений объединяются и записывают ответ.
Учимся решать уравнения с модулем методом промежутков. Рассмотрим пример.
Пример 1. Решим уравнение |х – 1| + |х – 2| = x. Решение. Выражения, стоящие под знаком модуля, обращаются в нуль при х = 1 и х = 2. Заметим, что такие числа часто называют нулями подмодульных выражений. Они разбивают координатную прямую на промежутки. В нашем случае первый промежуток включает в себя все точки, лежащие левее А; второй промежуток содержит в себе точки А и В, а также все точки, лежащие между ними; третий промежуток состоит из всех точек, лежащих правее В (рис.7 ). Заметим, что концы полученных промежутков можно относить к любому из смежных промежутков. Будем искать решения данного уравнения на каждом из промежутков. Для этого решим три системы:
1) Û . Решений нет.
2) Û Û (x = 1).
3) Û Û (x = 3).
Ответ: 1; 3. Практическая часть Задание 1. Возьмите чистый лист бумаги и на нем запишите ответы ко в сем устным упражнениям, приведенным ниже. Свои ответы сверьте с ответами или краткими указаниями, помещенными в конце учебного элемента в рубрике «Ваш помощник». Устные упражнения 1. Раскройте знак модуля: а) |–5|; б) |5|; в) |0|; г) |p|. 2.Как при помощи знака модуля записать, что по крайней мере одно из чисел а, b или с отлично от нуля ? 3.Как при помощи знака равенства записать, что каждое из чисел а, b и с равно нулю ? 4. Найдите значение выражения: а) |а| – а; б) а + |а|. 9. Существуют ли такие значения переменной х, при которых имеет место равенство: а) ïх – 5ï + ïх – 6ï = –7; б) –2ï7 – хï – 3ï1 + хï = 8; в) ïх – 2ï + ïх2 – 4ï = 0 ? 10.Пусть а – любое действительное число. Укажите множество решений уравнения ïхï = а в зависимости от а. 12.При каких значениях х имеет место равенство: а) ïхï = –х2; в) ïх – 1ï + ïх2 – 1ï = 0; б) ïхï = х2; г) ï5 + ï3 – хïï = 0. С некоторыми видами следующих заданий вы могли встречаться на уроках математики. Самоопределитесь, какие из следующих заданий вам необходимо выполнить. В случае затруднений обращайтесь к рубрике «Ваш помощник», за консультацией к учителю или за помощью к товарищу. Задание 2. Решите уравнение: а) |x – 1| + |x – 2| = 3; б) |x – 2| – 3|3 – x| + x = 0; в) |x + 5| + |x – 3| + |x – 1| = 0; г) |x + 2| + 3|1 – x| – 2|6x – 3| = –1; д) |3 – 2x| – |x + 1| + |2 – x| = |3 – 9x| + x – 5.
Рубрика «Ваш помощник» 1. а) 5; б) 5; в) 0; г) –p. 2. |а| + |b|+ |с| ¹ 0 либо а2 + b2+ с2 ¹ 0. 3. |а| + |b|+ |с| = 0 либо а2 + b2+ с2 = 0. 4. а) Если а ³ 0, то |а| – а = 0; если а < 0, то |а| – а = –2а.
9.а) не существует; б) не существует; в) существует, х = 2. 10 а при а > 0, 0 при а = 0; нет решений при а < 0. 12. а) при х = 0; б) при х = 0, х = –1, х = 1; в) при х = 1; г) таких значении х не существует. К заданию 2. а) 0; 3; б) УЭ-6. Решение уравнений вида |ах + b| = c Ваша цель: научиться решать уравнения |ах + b| = c, сводящиеся к совокупности уравнений. Входная информация Понятие о решении уравнений вида |ах + b| = c. При решении уравнений вида |ах + b| = c, (1)
где а, b и с – любые действительные числа, следует различать случаи, когда с < 0, с = 0, с > 0. 1) Если с < 0, то уравнение (1) не имеет корней, так как выражение |ах + b| при любом действительном х принимает только неотрицательные значения. 2) Если с = 0, то уравнение (1) равносильно уравнению ах + b = 0. 3) Если с > 0, то уравнение (1) равносильно совокупности уравнений:
т.е. (ах + b = c) Û , где с > 0.
Учимся решать уравнения с модулем. Пример 1. Решить уравнение |3x – 1| = 8. Решение. Имеем:
(|3x – 1| = 8) Û Û . Ответ: Форма записи решения может быть и другой, т.е без использования знака равносильности. Практическая часть Задание 1. Возьмите чистый лист бумаги и на нем запишите ответы ко в сем устным упражнениям, приведенным ниже. Свои ответы сверьте с ответами или краткими указаниями, помещенными в конце учебного элемента в рубрике «Ваш помощник». Устные упражнения 1. Вычислите: а) 2. Решите уравнение: а) |х| = 3; в) |х| = –2; д) |2х – 5| = 0; б) |х| = 0; г) |х – 3| = 4; е) |3х – 7| = – 9.
Задание 2. Решите уравнение: а) |x| = 1,3; г) |x – 1| = 3; ж) |3 – 4x| = 3; б) |x| = 0; д) |2x + 7| = 5; з) |5 + |x|| = 3; в) |x| = – 2,7; е) |4 – 5x| = 8; и) ||x| – 2| = 1. Задание 3. Найдите корни уравнения: а) ||x + 1| – 4| = 2; в) ||x– 1| – 1| = 1; б) |3 – |x + 1|| = 5; г) |2 – |1 – |x = 1. Рубрика «Ваш помощник» К заданию 2. 5.а) –3; 3; б) нет решений ; в)нет решений; г) –1; 7; д) 2,5; е) нет решений. К заданию 3. а) -1,3; 1,3; в) нет решений; г) -3; 3. К заданию 4. а)-7; -3; 1; 5. б) -9; 7; в) -3; -1; 1: 3; г) -4; -2; 0; 2; 4. УЭ-7. Решение уравнений вида |ах + b| = |cх + d|, |ах + b| = ах + b и |ах + b| = –(ах + b). Ваша цель: научиться решать уравнения данного вида Входная информация Решение уравнений вида |ах + b| = |cх + d|. При решении уравнения данного вида можно воспользоваться равносильностями:
1. (|ах + b| = |cх + d|) Û . Эта равносильность имеет место в силу свойства модуля: (|х| = |у|) Û .
2. (|ах + b| = |cх + d|) Û ((ах + b)2 = (cх + d)2). Эта равносильность имеет место в силу свойства модуля: (|х| = |у|) Û (х2 = у2). Пример 1. Решим уравнение |2х – 1| = |х + 3|. Решение. 1-й способ. Имеем: (|2х – 1| = |х + 3|) Û Û .
2-й способ. Имеем:
(|2х – 1| = |х + 3|) Û ((2х – 1)2 = (х + 3)2) Û ((2х – 1)2 – (х + 3)2 = 0) Û Û ((2х – 1 – х – 3) (2х – 1 + х + 3) = 0) Û Û ((x – 4) (3x + 2) = 0) Û . Ответ: Решение уравнений вида |ах + b| = ах + b и |ах + b| = –(ах + b). При решении уравнений данного вида целесообразно использовать равносильность: 1) (|ах + b| = ах + b) Û (ах + b ³ 0); 2) (|ах + b| = –(ах + b)) Û (ах + b £ 0).
В самом деле, если а – любое действительное число, то равенство |а| = а справедливо тогда и только тогда, когда а ³ 0, а равенство |а| = –а – тогда и только тогда, когда а £ 0. Поэтому уравнение |f(x)| = f(x), где f(x) выражение с одной переменной, равносильно неравенству f(x) ³ 0, а уравнение |f(x)| = – f(x) равносильно неравенству f(x) £ 0. Пример 2. Решить уравнение |3х – 9| = 3х – 9. Решение. Имеем: (|3х – 9| = 3х – 9) Û (3х – 9 ³ 0) Û (х ³ 3). Ответ: [3; + ¥).
Пример 3. Решить уравнение |2х – 5| = 5 – 2х. Решение. Множество решений данного уравнения совпадает с множеством решений неравенства 2х – 5 £ 0. Множество решений его представляет собой числовой промежуток (–¥; 2,5]. Ответ: (–¥; 2,5]. Практическая часть Задание 1. Возьмите чистый лист бумаги и на нем запишите ответы ко в сем устным упражнениям, приведенным ниже. Свои ответы сверьте с ответами или краткими указаниями, помещенными в конце учебного элемента в рубрике «Ваш помощник». Устные упражнения 1. Что можно сказать о числах х и у, если: а) |х| = х; б) |х| = –х; в) |х| = |у|? 2.Что можно сказать о числе у, если имеет место равенство: а) ïхï = у; б) ïхï = –у ? 3. Решите уравнение: а) |х – 2| = х – 2; в) |х – 3| =|7 – х|; б) |х – 2| = 2 – х; г) |х – 5| =|х – 6|. Задание 2. Решите уравнение: а) |x + 3| = |x – 5|; д) |x – 2| = 3|x + 3|; б) |3x – 5| = |x + 2|; е) |x + 3| = –|x2 – 9|; в) |x– 1| = |x – 2|; ж) |x + 2| = –|x2 – 16|; г) |x + 6| = |10 + x|; з) |x + 2| = |–x – 2|. Задание 3. Найдите корни уравнения: а) Задание 4. Решите уравнение: а) |x| = x; в) |2x – 3| = 2x – 3; б) |x| = –x; г) |2x – 3| = 3 – 2x. Рубрика «Ваш помощник» К заданию 1. Ответы к устным упражнениям: 1. а) х ³ 0; б) х £ 0; в) х = у или х = –у. 2. а) у ³ 0; б) у £ 0. 3. а) [2; +¥); б) (–¥; 2]; в) 5; г) 5, 5. К заданию 3. а) -4; УЭ-8. Решение уравнений вида |ах + b| = cх + d Ваша цель: научиться решать уравнения с модулем данного вида. Входная информация Способы решения уравнений вида |ах + b| = cх + d . При решении уравнений вида |ах + b| = cх + d можно поступать так: 1) применять метод промежутков; 2) использовать равносильности: (|ах + b| = cх + d) Û Пример 1. Решим уравнение |2х – 1| = 5х – 10. Решение. 1-й способ. Применим способ промежутков:
или
или
x= 3 Нет решений.
2-й способ. Имеем: (|2х – 1| = 5х – 10) Û Û Ответ: 3.
Практическая часть Задание 1. Возьмите чистый лист бумаги и на нем запишите ответы ко в сем устным упражнениям, приведенным ниже. Свои ответы сверьте с ответами или краткими указаниями, помещенными в конце учебного элемента в рубрике «Ваш помощник». Устные упражнения Решите уравнение: а) ïхï = –3; д) ïх + 1ï = –1; и) ïх – 7ï = ïх – 9ï; б) ïхï = 0; е) ïх – 1ï = 3; к) ïх – 3ï = х – 3; в) ïхï = 3; ж) ïх – 1ï = 0; л) ïх – 3ï = 3 – х; г) = 9; з) ïхï = ïх + 1ï; м) ï7хï – 7х = 0.
Задание 2 . Решите уравнение: а) |x– 1| = 3x + 2; г) |x + 1| – 2x =5; б) |x + 2| = 2x + 5; д) 3|x| – 5x = 2; в) |x – 2| = + 2x = 3; е) Задание 3. Найдите корни уравнения: а) б) в) Задание 4.Решите уравнение: а) б) Рубрика «Ваш помощник» К заданию 1.а) Нет решений; б) нет решений; в) –3; 3; г) –3; 3; д) нет решений; е) –2; 4; ж) 1; з) –0,5; и) 8; к) х ³ 3; л) х £ 3; м) х ³ 0. К заданию 2. а) К заданию 3. а) К заданию 4. а) 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ;
;  ; в) нет решений; г)
; в) нет решений; г) 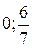 ; д)
; д)  ;
; 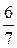 .
.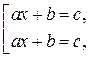
 .
. ; б)
; б)  ; в)
; в)  г)
г)  д)
д) 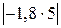 .
. .
. ; б) .
; б) . 
 ; 2; 4.
; 2; 4. .
. Û
Û Û (х = 3).
Û (х = 3). + 2x = .
+ 2x = . ; г)
; г)  ;
; ; д)
; д) 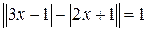 ;
; ; е)
; е)  .
. ; в)
; в) 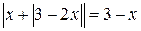 ;
;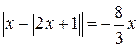 ; г)
; г)  .
.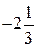 .
. ; в)
; в)  .
. .
.