
|
|
Если обе части верного неравенства умножить на одно и то же отрицательное число и изменить знак неравенства на противоположный, то получится верное неравенство.Следствие. Если а и b– положительные числа и а < b, то > .
Свойство 5. Если а < b и c < d, то a + c < b + d. Итак, если сложить почленно два верных неравенства одного знака и сохранить этот знак, то получится верное неравенство. Свойство 6. Если а < b и c > d, то a – c < b – d. Итак,два верных неравенства противоположного знака можно почленно вычитать, оставляя знак того неравенства, из которого вычитали другое неравенство. Свойство 7. Если а, b, с, d – положительные числа, а < b и c < d, то ac < bd. Итак,если перемножить почленно два верных неравенства одного знака, левые и правые части которых положительные числа, то получится верное неравенство, имеющее тот же знак, что и данное неравенство. Следствие 1. Если 0 < a < b, то an < bn, где n– натуральное число. Следствие 2. Если 0 < a < b, то < .
Практическая часть Задание 1. Возьмите чистый лист бумаги и на нем запишите ответы на все устные упражнения приведенные ниже. Затем свои ответы сверьте с ответами или краткими указания, помещенными в конце этого учебного элемента в рубрике «Ваш помощник». Устные упражнения 1. Верно ли неравенство: а) б) в) г) д) е) ж) з) и) к) л) м) 2. При каких значениях а) б) в) 3. Сравните действительные числа а) б) в) г) 4. Известно, что 5. Сравните а) б) в) 6. Верно ли неравенство: а) б) в) г) д) 7. Сравните числа а) б) в) г) д) 8. Известно, что а) б) в) г) д) 9. Как расположены на координатной прямой точки, изображающие а) б) в) г) 10. Объясните, почему можно утверждать, что неравенство верно при любых значениях переменной: а) б) в) г) 11. При каких значениях переменной а) б) в) 12. Укажите наибольшее целое а) б) в) г) д) е) ж) з) 13. Укажите наименьшее целое а) б) в) г) 14. Каким числом может быть а) б) в) г) 15. Каковы знаки чисел а) б) в) г) Задание 2. Сравните действительные числа Задание 3. Известно, что Задание 4. Может ли разность д) больше суммы е) меньше суммы ж) равна сумме з) больше и) больше к) равна Задание 5. Известно, что л) к обеим частям неравенства прибавить действительное число м) из обеих частей неравенства вычесть действительное число н) обе части неравенства умножить на о) обе части неравенства разделить на п) обе части неравенства разделить на Задание 6. Известно, что а) б) в) г) Задание 7 .Каков знак действительного числа р) с) т) у) Задание 8. Пусть а) б) Задание 9 .Верно ли, что: а) если б) если в)если г) если Задание 10. Сложите почленно неравенства: а) 21 > 3 и 13 > 4; в) 4 > –2 и –2 > –7; б) –2 < 5 и –7 < 3; г) –5 < –3 и –7 < –1. Задание 11.Вычтите почленно из первого неравенства второе: а) 3 < 5 и 7 > 1; в) 14 > –3 и –3 < –2; б) 11 > 4 и –2 < 5; г) –13 > –10 и –6 > –17. Задание 12.Перемножьте почленно неравенства: а) 7 < 8 и 2 < 3; в) 15 > 11 и 5 > 4; б) 18 > 7 и 3 > 2; г) 2 < 21 и 3 < 5. Задание 13. Пусть а > 2, b > 3, c > 1. Докажите, что: а) а + b + c > 6; в) 2аb + 3 аbc > 30; б) abc > 6; г) a2 + b2 + c2 > 13. Задание 14.Докажите, что: а) если а > 2 и b > 5, то 5а + 2b > 20; б) если а > 3, то a2 + 6 ³ 15; в) если а > b, то 1 – а < 2 – b. Задание 15.Верно ли утверждение: а) если одно действительное число больше другого, то и куб первого числа больше куба второго; б) если модуль одного действительного числа больше модуля другого, то и квадрат первого числа больше квадрата второго? Задание 16.Пусть а > b и числа а, b – отрицательные. Докажите, что: а) аn > bn, если n – нечетное натуральное число; б) аn < bn, если n – четное натуральное число. Задание 17.Значение какого выражения больше: а) + или + 3;
б) – или – ;
в) + + или + + ;
г) или ?
Задание 18.Пусть а – некоторое действительное число. Что больше: а) а или 3а; б) а или а2? Задание 19.9 ручек стоят дороже, чем 11 карандашей. Что дороже – 15 ручек или 17 карандашей? Задание 20. Пассажир сдает в багажное отделение рюкзак, чемодан, саквояж и корзинку. Чемодан тяжелее, чем рюкзак, саквояж и рюкзак тяжелее, чем корзинка и чемодан, а корзинка и саквояж вместе весят столько, сколько вместе весят чемодан и рюкзак. Какой из этих грузов самый тяжелый, а какой самый легкий?

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
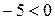 ;
; ;
; ;
;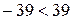 ;
;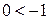 ;
;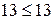 ;
;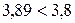 ;
; ;
; ;
; ;
;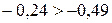 ;
; ?
?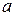 верно неравенство:
верно неравенство: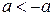 ;
;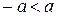 ;
; ?
?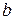 , если
, если  равно:
равно: ;
; ;
; ;
;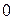 .
. . Может ли разность
. Может ли разность  выражаться числом:
выражаться числом: 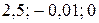 ?
? , если
, если  . Рассмотрите случаи:
. Рассмотрите случаи: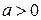 ;
; ;
; .
.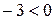 ;
; ;
;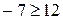 ;
;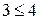 ;
;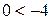 ?
? ;
; ;
;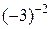 .
.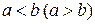 . Может ли разность
. Может ли разность  ;
;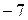 ;
; ;
;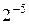 ;
;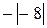 ?
? ;
; ;
;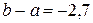 ;
; ?
? ;
; ;
; ;
;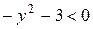 .
. ;
;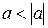 ;
;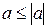 ?
? , удовлетворяющее неравенству:
, удовлетворяющее неравенству: ;
;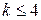 ;
;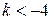 ;
;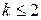 ;
;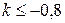 ;
; ;
;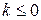 ;
; .
.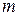 , удовлетворяющее неравенству:
, удовлетворяющее неравенству: ;
; ;
; ;
;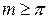 .
. , если:
, если: ;
; ;
; ;
;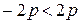 ?
?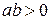 ;
;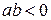 ;
;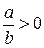 ;
; ?
? .
.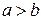 . Может ли разность
. Может ли разность  ?
? ;
; , где
, где  ;
;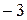 ;
;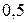 ;
; .
.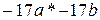 ;
;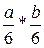 ;
;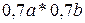 ;
;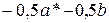 .
.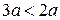 ;
; ;
;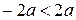 ;
;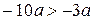 ?
? . Докажите, что:
. Докажите, что: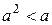 ;
;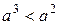 .
.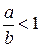 ;
; ;
; , то
, то  , то
, то