
|
|
УЭ-3. Числовые промежуткиВаша цель: знать определения, уметь обозначать и изображать на координатной прямой различные числовые промежутки; записывать промежутки, изображенные на координатной прямой, в виде неравенства, указывать числа, принадлежащие и не принадлежащие данному промежутку; находить пересечение и объединение промежутков и записывать их с использованием знаков Входная информация Основные понятия темы. Они представлены в виде таблицы.
Практическая часть Задание 1. Возьмите чистый лист бумаги и на нем запишите ответы на все устные упражнения приведенные ниже. Затем свои ответы сверьте с ответами или краткими указания, помещенными в конце этого учебного элемента в рубрике «Ваш помощник». Задание 2. Изобразите на координатной прямой промежуток: а) [–1; 3]; б) (–2; 2); в) (1; ¥); г) [3; ¥); д) (–¥; 4); е) (–¥; –2]; ж) (–¥; +¥). Задание3. Запишите промежутки, изображенные на рисунке 20, в виде неравенства. Задание 4. Принадлежит ли промежутку [–4,5; p) число –3; –7; 0; 3,14; 9,1? Задание 5. Укажите два положительных и два отрицательных рациональных числа, принадлежащих промежутку: а) (–1; 1); б) [–4; 8). Задание 6. Какие из целых чисел принадлежат промежутку: а) [–2; 2]; б) (–5,2; 6,25]; в) (–3; –2); г) (–1; 0)? Задание 7. Укажите наибольшее или наименьшее целое число, принадлежащее промежутку: а) [–4; 5]; б) [–2,3; 1,7); в) (–¥; 24]; г) (–3; +¥). Задание 8. Используя координатную прямую, найдите пересечение промежутков: а) [1; 7] и [2; 4]; г) (3; +¥) и (–¥; 2); б) (1; 5) и (2; 4); д) (–3; +¥) и (4; +¥); в) [–2; 3) и (–7; 2); е) (–¥; +¥) и (p; 5). Задание 9. Покажите штриховкой на координатной прямой объединение промежутков: а) [5; 9] и [–3; 5]; в) [5; +¥) и (3; +¥); б) [3; 7) и [7; 10]; г) [1; 3] и (–6; 2). Задание 10. Используя координатную прямую, найдите пересечение и объединение промежутков: а) [–5; 3] и [–3; 7]; в) (–¥; 3] и (1; +¥); б) (1; 0) и [0; 5]; г) [–7; 12] и [3; 4]. Задание 11. Пусть Z0– множество целых чисел х, таких, что –12 £ x £ –3. Выпишите его элементы. Задание 12. Изобразите на координатной прямой множество всех целых чисел, принадлежащих отрезку [–5; 5]. Задание Выпишите из множества {1,41; 1,414; 1,42; 1,415; 1,73; 1,732; 1,74; 1,7333} все элементы, которые принадлежат промежутку (; ). Задание Выпишите из множества {1,41; 1,414; 1,42; 1,415; 2,42; 2,428; 2,43; 2,429} все элементы, которые принадлежат промежутку (; ). Задание 15.Сколько рациональных и иррациональных чисел содержит промежуток (; ). Задание 16. Пусть 0 < a < b. Докажите, что на координатной прямой: а) точка – середина отрезка [а; b]; б) точка – середина отрезка [–b; а]; в) точка – середина отрезка [–а; b]; г) точка – середина отрезка [–b; –a]; УЭ-4. Решение задач по теме «Линейное неравенство с одной переменной» Ваша цель: знать определения понятий «линейное неравенство», «решение неравенства», «равносильные неравенства»; знать, что значит решить неравенство; знать и уметь применять утверждения, на основе которых осуществляются равносильные переходы; уметь решать линейные неравенства в общем виде. Входная информация Понятие линейного неравенства. Напомним, что называют линейным неравенством. Неравенства вида ах > b, ах < b, ах ³ b, ах £ b, где а и b – некоторые действительные числа, х – переменная, называются линейными. Примерами линейных неравенств являются: 2x > 3, 7х < 8, х > 3, 0,5x < –1. Что значит решить неравенство. Решением неравенства с одной переменной называется значение переменной, которое обращает его в верное числовое неравенство. Например, число 1 – решение неравенства 7x < 8, так как 7$1 < 8 –верное числовое неравенство. Решить неравенство – значит найти все его решения или доказать, что решений нет. Например, неравенство 0 Понятие равносильности неравенств. Важно знать и понимать определения понятия равносильности неравенств. Неравенства, имеющие одни и те же решения, называются равносильными. Неравенства, не имеющие решений, также считают равносильными. Решение линейного неравенства в общем виде. Пусть дано неравенство ах > b. Если а > 0, то неравенство ах > b равносильно неравенствух> (свойство 2), значит, множество решений неравенства есть промежуток Если а < 0, то неравенство ах > b равносильно неравенству х < (свойство 3), и поэтому множество решений неравенства есть промежуток (–¥; ). Если а = 0, то неравенство принимает вид 0 Алгоритм решения линейного неравенства в общем виде показан в таблице 3.
Таблица 3
Практическая часть
Задание 1. Возьмите чистый лист бумаги и на нем запишите ответы на все устные упражнения приведенные ниже. Затем свои ответы сверьте с ответами или краткими указания, помещенными в конце этого учебного элемента в рубрике «Ваш помощник». Устные упражнения 1. Какие из чисел 2. Являются ли равносильными неравенства: а) б) в) г) д) е) 3. Решите неравенство: а) б) в) г) д) е) 4. Укажите множество решений неравенства: а) б) в) г) д) е) 5. Решите неравенство: а) б) в) г) д) е) ж) з) и) 6. Какова область определения выражения: а) б) в) г) 7. Укажите множество решений неравенства: а) б) в) г) д) е) ж) з) и) 8. Решите уравнение: а) б) в) г) 9. Какие из чисел 10. Являются ли равносильными неравенства: а) б) в) г) д) е) 11. Решите неравенство и изобразите множество его решений на координатной прямой: а) б) в) г) д) е) ж) з) и) к) л) м)
Задание 2. Какие из чисел –5,1; ; –8; 0; 1,7 являются решением неравенства 3х <1? Задание 3. Являются ли равносильными неравенства: а) х – 2 < 2х и –x < 2; г) –х < 5 их> –5; б) x < 4 и 2x < 8; д) –4x < –8x и х < 2; в) –x < 3 и х < –3; е) 0$х > 3 и –7 > 0$х? Задание 4. Решите неравенство и изобразите множество его решений на координатной прямой: а) 3x > 18; д) 7t >0; и)3k > –1; б) –4x > 5; е) –4t > 0; к) –3k > –1; в)2x £ –1; ж) –2t > –8; л) 0$k ³ –2; г) –0,4x £6; з) –3t < –9; м) –2k ³ 0.
Рубрика «Ваш помощник» К заданию 1.Ответы к устным упражнениям: 1. 1и 10. 2. а) да; б) нет; в) да; г) нет; д) да; е) нет. 3. а) 4. а) 5. а) 6. а) 7. а) 8. а) 9. 10. а) да; б) да; в) нет. 11. а)

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 .
.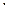 х > 1 не имеет решений, поскольку при любом действительном х получается неверное числовое неравенство.
х > 1 не имеет решений, поскольку при любом действительном х получается неверное числовое неравенство.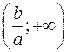 .
. являются решением неравенства
являются решением неравенства  ?
?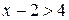 и
и  ;
;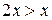 и
и 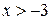 ;
;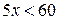 и
и 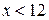 ;
;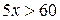 и
и 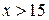 ;
;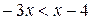 и
и  ;
; и
и  ?
? ;
;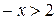 ;
;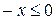 ;
; ;
; ;
; .
.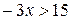 ;
; ;
;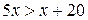 ;
;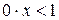 ;
;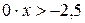 ;
;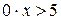 .
.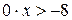 ;
;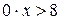 ;
;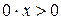 ;
;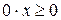 ;
; ;
;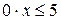 ;
;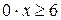 ;
;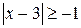 ;
;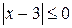 .
.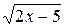 ;
; ;
;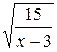 ;
;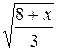 ?
? ;
;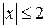 ;
; ;
; ;
;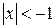 ;
; ;
; ;
; ;
;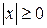 .
. ;
;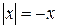 ;
;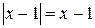 ;
; .
.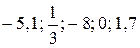 являются решением неравенства
являются решением неравенства 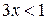 ?
?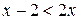 и
и 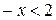 ;
;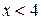 и
и 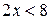 ;
;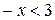 и
и  ;
;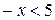 и
и  ;
;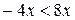 и
и  ;
; и
и  ?
?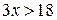 ;
;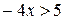 ;
;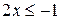 ;
;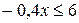 ;
;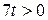 ;
;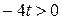 ;
;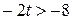 ;
; ;
; ;
;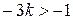 ;
; ;
;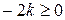 .
.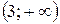 ; б)
; б) 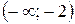 ; в)
; в) 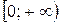 ; г)
; г) 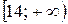 ; д)
; д)  ; е)
; е)  .
.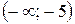 ; б)
; б) 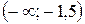 ; в)
; в) 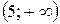 ; г)
; г)  ; д)
; д)  б) Ø; в) Ø; г)
б) Ø; в) Ø; г) 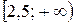 ; б)
; б) 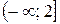 ; в)
; в) 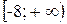 .
. ; б)
; б)  ; в) {0}; г) Ø; д) Ø; е)
; в) {0}; г) Ø; д) Ø; е) 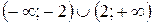 ; ж)
; ж) 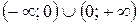 ; и)
; и)  ; в)
; в) 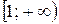 ; г)
; г)  .
.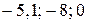 .
. ; б)
; б) 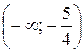 ; в)
; в)  .
.