
|
|
УЭ-2. Доказательства неравенствВаша цель: знать методы доказательства неравенств и уметь их применять. Практическая часть Понятие доказательства неравенства. Некоторые неравенства обращаются в верное числовое неравенство при всех допустимых значениях переменных или на некотором заданном множестве значений переменных. Например, неравенства а2³0, (а–b)2 ³ 0, a2 + b2 + c2 '³ 0 верны при любых действительных значениях переменных, а неравенство ³ 0 – при любых действительных неотрицательных значениях а. Иногда возникает задача доказательства неравенства. Доказать неравенство – значит показать, что данное неравенство обращается в верное числовое неравенство при всех допустимых значениях переменных или на заданном множестве значений этих переменных.
Методы доказательства неравенств. Заметим, что общего метода доказательства неравенств не существует. Однако некоторые из них можно указать. 1. Метод оценки знака разности между левой и правой частями неравенства. Составляется разность левой и правой частей неравенства и устанавливается, положительна или отрицательна эта разность при рассматриваемых значениях переменных (для нестрогих неравенств надо установить, неотрицательна или неположительна эта разность).
Пример 1. Для любых действительных чисел а и b имеет место неравенство a2+b2 ³ 2ab. (1) Доказательство. Составим разность левой и правой частей неравенства: a2+b2 – 2ab = a2 – 2ab + b2 = (a – b)2. Так как квадрат любого действительного числа есть число неотрицательное, то (a – b)2³ 0, а, значит, a2+b2 ³ 2ab для любых действительных чисел а и b. Равенство в (1) имеет место в том и только в том случае, когда а = b. Пример 2. Доказать, что если а ³ 0 и b ³ 0, то ³ , т.е. среднее арифметическое неотрицательных действительных чисел а и b не меньше их среднего геометрического. Доказательство. Если а ³ 0 и b ³ 0, то – = = = ³ 0. Значит, ³ . 2. Дедуктивный метод доказательства неравенств. Сущность этого метода заключается в следующем: с помощью ряда преобразований выводят требуемое неравенство из некоторых известных (опорных) неравенств. В качестве опорных могут использоваться, например, неравенства: а2 ³ 0 при любом a Î R; (a – b)2 ³ 0 при любых а и b Î R; (а2 + b2) ³ 2ab при любых a, b Î R; ³ при а ³ 0, b ³ 0. Пример 3. Доказать, что для любых действительных чисел а и b имеет место неравенство а2 + b2 + с2 ³ ab + bc + ac. Доказательство. Из верных неравенств (a – b)2 ³ 0, (b – c)2 ³ 0 и (c – a)2 ³ 0 следует, что а2 + b2 ³ 2ab, b2 + c2 ³ 2bc, c2 + a2 ³ 2ac. Сложив почленно все три неравенства и разделив обе части нового на 2, получим требуемое неравенство. Исходное неравенство можно доказать и первым методом. В самом деле, а2 + b2 + с2 – ab – bc – ac = 0,5(2а2 + 2b2 + 2с2 – 2ab – 2bc – 2ac) = = 0,5((a – b)2 + (a – c)2 + (b – c)2)³ 0. Разность между а2 + b2 + с2 и ab + bc + ac больше или равна нулю, а это значит, что а2 + b2 + с2 ³ ab + bc + ac (равенство справедливо тогда и только тогда, когда а = b = с). 3. Метод оценок при доказательстве неравенств. Пример 4. Доказать неравенство + + + … + > Доказательство. Легко заметить, что левая часть неравенства содержит 100 слагаемых, каждое из которых не меньше . В таком случае говорят, что левую часть неравенства можно оценить снизу следующим образом: + + + … + > 4. Метод полной индукции. Сущность метода состоит в рассмотрении всех частных случаев, охватывающих условие задачи в целом. Пример 5. Доказать, что если х > ïуï, то х > у. Доказательство. Возможны два случая: а) у ³ 0; тогда ïуï = у, а по условию х > ïуï. Значит, х > у; б) у < 0; тогда ïуï > у и по условию х > ïуï, значит, х > у.
Практическая часть Задание 0. Возьмите чистый лист бумаги и на нем запишите ответы на все устные упражнения приведенные ниже. Затем свои ответы сверьте с ответами или краткими указания, помещенными в конце этого учебного элемента в рубрике «Ваш помощник».
Устные упражнения 1. Сравните сумму квадратов двух неравных чисел 2. Докажите неравенство: а) б) в) г) 3. Известно, что 4. Известно, что Задание 1. Что больше: а) 2 + 11 или 9; г) + или ; б) или + ; д) – или ; в) + или 2; е) + 2 или + ? Задание 2. Докажите, что при любом действительном x имеет место неравенство: а) 3(x + 1) + x – 4(2 + x) < 0; г) 4x2 + 1 ³ 4x; б) (x + 2)(x + 4) > (x + 1)(x + 5); д) ³ 2x; в) (x – 2)2 > x(x – 4); е) l + 2x4 > x2 + 2x3. Задание 3. Докажите, что: а) x3 + 1 ³ x2 + x, если x ³ –1; б) x3 + 1 £ x2 + x, если x £ –1. Задание 4. Докажите, что если a ³ 0, b ³ 0, с ³ 0, d ³ 0, то (a2 + b2)(c2 + d2) ³ (ac + bd)2. Задание 5. Докажите неравенство, выделив полный квадрат: а) x2 – 2xy + 9y2 ³ 0; б) x2 + y2 + 2³2(x + y); в) 10x2 + 10xy + 5y2 + 1 > 0; г) x2 – xy + y2 ³ 0; д) x2 + y2 + z2 + 3³ 2(х + у + z); e) (x + l)(x – 2y + l) + y2 ³ 0. Задание 6. Докажите, что: а) x2 + 2y2 + 2xy + 6y + l0 > 0; б) x2 + y2 – 2xy + 2x – 2у + 1 > 0; в) 3x2 + y2 + 8x + 4y – 2xy + 22 ³ 0; г) x2 + 2xy + 3y2 + 2x + 6y + 3 > 0. Задание 7. Докажите, что если n ³ k ³ 1, то k(n – k + 1) ³ n. Задание 8. Докажите, что если 4а + 2b = 1, то a2 + b2 ³ . Определите значения а и b, при которых имеет место равенство. Задание 9. Докажите неравенство: а) х3 + у3 ³ х2у + ху2 при x ³ 0 и y ³ 0; б) х4 + у4 ³ х3у + ху3 при любых x и у; в) х5 + у5 ³ х4у + ху4 при x ³ 0 и y ³ 0; г) хn + уn ³ хn-1у + хуn-1 при x ³ 0 и y ³ 0. Задание 10. Верно ли, что: а) если а2b ³ 0, то b ³ 0; б) если а2b > 0, то b > 0? Задание 11. Докажите неравенство:
а) < 2;
б) < 6. Задание 12. Докажите, что: а)
б) Задание 13. Докажите, что: а) + + … + + > 4 б) + + + … + < 0,99; в) + + … + < 0,999.
Задание 14. Что больше: а) 12710 или 10257; в) 3200 или 2300; б) 5336 или 3653; г) 9920 или 999910? Задание 15. Докажите, что при любом действительном х имеет место неравенство: а) x12 – x9 + x4 – x – 1 > 0; б) x8 – x6 – 4x4 – x2 – 1> 0. Рубрика «Ваш помощник» К заданию 0.Ответы к устным упражнениям: 1. 2. а) 3. 4. Так как

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
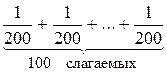 =
= 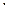 100 = .
100 = .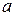 и
и 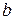 с их удвоенным произведением.
с их удвоенным произведением.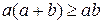 ;
; ;
; ;
;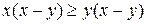 .
.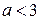 . Докажите, что
. Докажите, что 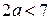 .
. . Докажите, что
. Докажите, что 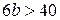 .
.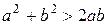 , так как
, так как  .
.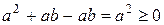 ; б)
; б) 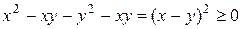 .
.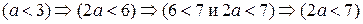 .
.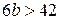 , но
, но  , значит,
, значит,