|
|
ЧИСЛОВЫЕ И ЛИНЕЙНЫЕ НЕРАВЕНСТВАК.О. Ананченко Алгебра учит рассуждать, доказывать и решать задачи: Класс Учебное пособие Для факультативных занятий по математике
Информация для учащихся Уважаемые ученики! Вы изучаете факультативный курс математики, который предполагает более высокий уровень овладения учебным материалом, чем на уроках математики 8 класса. Для вас важно научиться: ü точно и грамотно формулировать изученные теоретические положения (определения, теоремы, правила и т.д.); ü правильно пользоваться математической терминологией и символикой; ü решать стандартные и нестандартные задачи; ü использовать общие и частные эвристические приемы по поиску решения новых задач; ü рассуждать и доказывать. Для достижения данных целей возрастает роль теоретических знаний, становятся весьма значимыми такие их качества как полнота и глубина, оперативность и гибкость, конкретность и обобщенность, системность и осознанность, прочность. Важное место в процессе изучения факультативного курса будет занимать самостоятельная математическая деятельность. Успешность ее выполнения зависит от овладения обобщенными способами самостоятельной учебной деятельности. Вы должены стремиться к тому, чтобы ваши умения и навыки по выполнению тех или иных алгебраических действий удовлетворяли таким требованиям, как: правильность (без ошибок и недочетов выполнять все операции, входящие в действие); осознанность (уметь указать или формулировать правило, теорему, формулу в соответствии с которой действуешь); автоматизм (каждую операцию выполнять быстро, свернуто); рациональность (выбирать наиболее короткий, ''экономный'' путь действия), обобщенность (уметь выполнить действие в различных ситуациях); прочность (сохранять в течение длительного времени приобретенные умение или навыки).
Процесс решения задач включает следующие взаимно связные этапы: ü анализ задачи (стандартной или нестандартной); ü принятие решения относительно способа деятельности, соответствующего этой задаче в форме: а) либо однозначного способа деятельности; б) либо выбора более результативного из возможных альтернативных способов; в) либо конструирование способа деятельности в отношении нестандартной ситуации; ü исполнение решения; ü контроль и самоконтроль. Данная модульная программа позволяет приобрести определенный опыт самостоятельной учебной деятельности, самоопределиться и оценить свои возможности овладения учебным материалом. Рассмотрим основные структурные элементы модульной программы. Модуль учебной программы. Вся программа состоит из модулей. Их число определяется целями обучения, содержанием и объемом учебного материала. Наименование модулей рассматриваемой программы следующее. Модуль 1. Числовые и линейные неравенства Модуль 2. Действительные числа Модуль 3. Арифметический квадратный корень Модуль 4. Квадратные уравнения. Уравнения, сводящиеся к квадратным уравнениям
Модули этой программы охватывают в комплексе все аспекты содержания факультативных занятий по алгебре. Каждый учебный модуль представляет собой законченный блок информации, целевую программу действий и методическое руководство по ее реализации. Его можно рассматривать как программу обучения, индивидуализированную по содержанию, уровню самостоятельности, темпу учебной деятельности ученика. Учебные элементы (УЭ). Каждый модуль разбит на учебные элементы. Их число определяется содержанием, объемом материала учебного модуля и логикой изложения. Так полный перечень учебных элементов представлен в содержании данного учебного пособия. В предлагаемой модульной программе каждый учебный элемент включает целевую установку, теоретическую и практическую части. Ваша цель. Она формулируется для каждого учебного элемента и адресована вам. Входная информация. Она, как правило, содержит учебный материал, с которым вы познакомились на уроке. Поэтому он представлен кратко: или в виде учебного приема, или логических схем, или в виде сущности некоторых теоретических фактов, которые напоминаются посредством примеров. В этой части модульной программы, как правило, представлено достаточное количество примеров решенных алгебраических задач, которые могут служить примерным оформлением решения задач в самостоятельных и контрольных (экзаменационных) работах. Практическая часть. Здесь посредством системы задач идет углубление и расширение учебного материала, изученного на уроках математики. Она состоит из заданий, направленных на: систематизацию и обобщение знаний; выработку алгебраических умений и навыков, удовлетворяющих такими требованиям, качествами, как правильность, осознанность, рациональность, автоматизм, обобщенность и прочность; формирование интеллектуальных умений; коррекцию усвоенных знаний, способов деятельности и на контроль за их усвоением.
Каждый модуль завершается рубрикой «Математическая мозаика». В ней вы найдете исторические сведения, интересные факты связанные с математикой, софизмы, шутки.
Технология модульного обучения позволяет кардинально поменять вашу роль и учителя в учебном процессе. Вы учитесь самостоятельно (или с определенной дозой помощи), а учитель организует, координирует, консультирует, контролирует вашу учебную деятельность. В каждом учебном элементе вы встретишься с рубрикой «Ваш помощник». В ней имеются ответы к некоторым заданиям, краткие указания, или полное решение, в противоположном случае (т.е. если они отсутствуют, учишься самоконтролю; обращаешься за помощью к товарищу, за консультацией к учителю). Алгебра есть не что иное, как математический язык, приспособленный для обозначения отношений между количествами. И. Ньютон Модуль 1. ЧИСЛОВЫЕ И ЛИНЕЙНЫЕ НЕРАВЕНСТВА
УЭ-1. ЧИСЛОВЫЕ НЕРАВЕНСТВА И ИХ СВОЙСТВА Ваша цель: уяснить смысл понятия «числовое неравенство», знать свойства числовых неравенств и уметь их применять при доказательствах и решении задач. Входная информация Понятие числового неравенства. Для любых неравных действительных чисел а и При решении многих задач важную роль играют следующие утверждения: 1. Два действительных числа а и b(обозначают: 2. Число а больше числа b (обозначают:а > b) тогда и только тогда, когда разность а – b положительна, т. е. а – b > 0. 3. Число а меньше b (обозначают а < b) тогда и только тогда, когда разность а – b отрицательна, т. е. а – b < 0. Пример 1. Докажем, что 9920 < 999910. Составим разность данных чисел и оценим ее: 9920 – 999910 = 9910 = 9910 Следовательно, 9920 < 999910. Пример 2. Докажем, что если |а| < e (e > 0), то –e < а < e. Если а – неотрицательное число, то |а| = аи а < e.С другой стороны, по условию e – положительное число; тогда –e отрицательное число. И так как а неотрицательное число, то –e < а. Из того, что –e < а и а < e следует, что –e < а < e. Если а – отрицательное число, то |а| = –а и –а < e, т.е. –e < а. Кроме того, а < 0, а e > 0, тогда а < e. В этом случае из того, что –e < а и а < e, следует, что –e < а < e. Обратное утверждение также верно. Пусть –e < а < e. Докажем, что |а| < e. Если а > 0, то а = |а|. И из условия а < e получаем |а| < e. Если же а < 0, то –а = |а|. Из условия –e < а следует |а| < e.
Свойства числовых неравенств. Перечислим теоремы, выражающие свойства некоторых числовых неравенств (буквами здесь обозначены действительные числа). Свойство 1. Если а < b, то b > а; если а > b, то b < а. Свойство 2. Если а < b и b < с, то а < c. Свойство 3. Если а < b и с – любое действительное число, то а + с < b + с. Итак,если к обеим частям верного неравенства прибавить одно и то же число, то получится верное неравенство. Следствие. Любое число можно перенести из одной части неравенства в другую с противоположным знаком. Свойство 4. Если а < b и с – положительное число, то ас < bс. Если а < b и с – отрицательное число, то ас > bс. Итак,если обе части верного неравенства умножить на одно и то же положительное число и сохранить знак исходного неравенства, то получится верное неравенство; 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
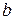можно сказать, какое больше, а какое меньше.
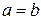) равны тогда и только тогда, когда их разность равна нулю, т. е. а – b = 0.
9910 – (99