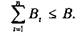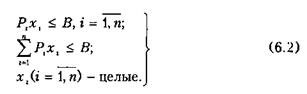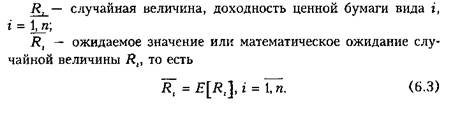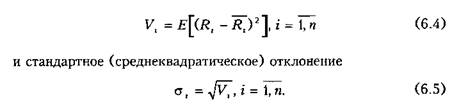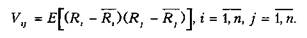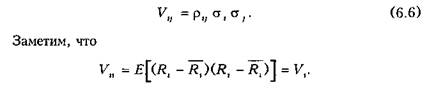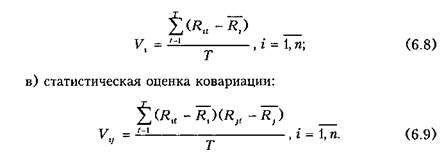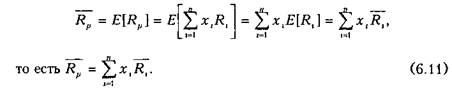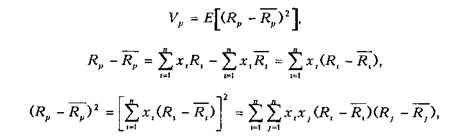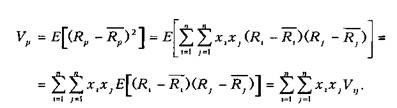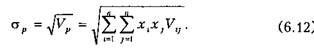Оптимизация портфеля ценных бумаг

Главный принцип формирования оптимального портфеля состо­ит в диверсификации ценных бумаг по видам с учетом ликвидности, доходности и риска. Поэтому рассмотрим методику наилучшего вы­бора структуры портфеля, то есть способы определения доли капи­тала для вложения в каждый из образующихся на рынке видов цен­ных бумаг.

На финансовом рынке имеется возможность приобретения лю­бого из видов различных ценных бумаг, каждая из которых имеет свою цену приобретения Рр_лри этом ожидаемая доходность бума­ги вида г составляет с,, г = 1, п. Для осуществления инвестиций ин­вестор располагает некоторой суммой В. Необходимость соблюде­ния требований диверсификации независимо от доходности цен­ной бумаги влияет на его решение не вкладывать в ценные бумаги вида г больше, чем В_г (г = 1, п) единиц средств. Очевидно, что

Построим математическую модель для этой ситуации.

Пусть х_г (г = 1, п) — количество ценных бумаг вида г, приобрета­емых инвестором. Тогда общий доход инвестора V от приобретения всех видов ценных бумаг составит

Методы решения данной задачи широко известны и здесь не об­суждаются.

Однако в реальной практике ситуация значительно сложнее. Это обусловлено тем, что многие параметры (такие, например, как ожидаемая доходность, вероятность ее получения и т.д.) инвестору заранее не известны. Поэтому рассмотрим более общую задачу фор­мирования оптимального портфеля, связанную с влиянием случай­ных факторов.

Очевидно, что построение любой модели возможно лишь при упрощении реальной ситуации. В основе современной теории порт­фельных инвестиций лежат предположения:

1. Инвесторы оценивают активы только по двум параметрам:

а) ожидаемой доходности;

б) среднеквадратическому отклонению доходности от ожидае­
мой величины.

2. Все инвесторы имеют свободный доступ к финансовым ак­
тивам.

3. Отсутствуют операционные издержки и налоги.

4. Нет ограничений на короткие продажи.

5. Существует безрисковая ставка процента, по которой инвес­
торы могут как инвестировать, так и брать кредит.

6. Активы бесконечно делимы. \
Данные предположения могут показаться достаточно жестки­
ми, но они вполне приемлемы для получения практических
решений.

Основной математический постулат, на котором будет строиться последующая теория, — это то, что доходность ценной бумаги явля­ется случайной величиной, а конкретное значение доходности — ре­ализацией этой случайной величины.

Для построения математической модели стоимости портфеля введем обозначения.

Дисперсия или вариация доходности г-й ценной бумаги будет равна

Здесь и далее используется операция вычисления математичес­кого ожидания £"[•], применяемого к случайной величине, стоящей в скобках. Ожидаемое значение случайной величины обычно пони­мается как среднее по всем значениям (реализациям), вычисленное с учетом частоты их возможного появления.

Среднеквадратическое отклонение доходности г'-й ценной бу­маги (г = 1, п) от ее математического ожидания является мерой риска ценной бумаги. Если вариация равна нулю, то есть У_£= 0, а следовательно и a _t = 0, то в этом случае неопределенность отсут­ствует, а значит и риск тоже. Чем больше вариация, тем больше Среднеквадратическое отклонение, тем больше доходность откло­няется от своего ожидаемого значения, тем выше неопределен­ность, тем выше риск.

В чем интерес инвестора? С одной стороны, для него важно получить максимальную эффективность от вложения своего капи­тала в ценные бумаги. С другой стороны, он заинтересован в по­лучении гарантий, что его ожидания сбудутся, поэтому важно уменьшить риск.

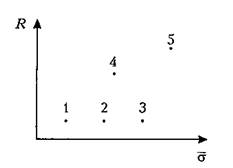
Очевидно, что ценная бумага, представленная точкой 1, являет­ся более предпочтительной по сравнению с ценными бумагами, представленными точками 2 и 3. Также бумага, представленная точ­кой 4, является более предпочтительной по сравнению с бумагой, представленной точкой 2. И только склонность к риску даст воз­можность выбора между бумагами, представленными точками 1, 4 или 5.

Рис. 6.1. Представление характеристик различных ценных бумаг

Для дальнейшего рассмотрения вопроса введем понятие ковари-ации двух случайных величин (V_tJ):

Ковариация характеризует зависимость двух случайных вели­чин: если V_l} > О, то увеличение одной случайной величины ведет к увеличению другой случайной величины, то есть имеет место пря­мая зависимость величин; если V_tj < О, то увеличение одной величи­ны ведет к уменьшению другой величины — имеет место обратная зависимость; в случае независимости двух случайных величин

у„ = о.

Ковариация связана с коэффициентом корреляции формулой

Для того чтобы получить ту или другую характеристику, ис­пользуются соответствующие статистические данные.

Пусть R_lt — доходность г-й (г = 1, п) ценной бумаги в периоде £, где t = 1, Г; Т — число наблюдаемых периодов. Тогда статистичес­кие оценки ценной бумаги будут вычисляться следующим образом:

а) статистическая оценка математического ожидания:

Перейдем к рассмотрению характеристик портфеля ценных бу­маг. Для этого важно знать его структуру, то есть соотношение до­лей капитала, вложенного в ценные бумаги различных видов.

Переходя к математическому ожиданию, на основании (6.10) получаем

Дисперсия, или вариация эффективности портфеля рассчиты­вается следующим образом:

Как и в случае с мерой риска для отдельной ценной бумаги, для портфеля такой же мерой риска будет являться среднеквадрати-ческое отклонение, то есть

Рассмотрим следующую ситуацию, когда инвестиционные ресур­сы разделены между всеми видами ценных бумаг поровну, то есть

Подставим (6.14) в (6.13), в результате получим инвестицион­ный риск, равный

На основании чего можно сделать вывод: при до( пншючн шом числе ценных бумаг, включенных в портфепъ, /ни л ограничен и стремится к нулю при п -> ос.

Этот результат известен в теории вероятностей как закон боль­ших чисел, а в теории финансовых рисков — как эффект диверси­фикации.

Отсюда вытекает основное практическое правило работы на фи­нансовом рынке: для повышения надежности эффекта от вклада в рискованные ценные бумаги целесообразно сделать вложения не в один вид, а сформировать портфель, содержащий возможно большее разнообразие ценных бумаг, эффект от которых случа­ен, но случайные отклонения независимы.

Полученные выводы сделаны на основании гипотезы о незави­симости эффектов. Рассмотрим случай, когда доходности ценных бумаг являются зависимыми случайными величинами. Подставим выражение (6.6) в (6.12) и получим'

Таким образом, при полной прямой корреляции диверсифика­ция не дает положительного эффекта, то есть риск портфеля не за­висит от числа ценных бумаг и не стремится к нулю при увеличении числа видов ценных бумаг. В результате проведенного анализа сле-

дует: чем меньше корреляция между доходностями ценных f)t/*ui/_t тем больше возможности снижения риска путем диверсификации портфеля.

Естественно, что ожидаемая эффективность и риск портфеля будут зависеть от его структуры, то есть доли исходного каптала, вложенного в каждый из видов ценных бумаг. Инвестор всегда сталкивается с дилеммой — желанием сформировать портфель с возможно большей ожидаемой эффективностью и в то же время воз­можно меньшим риском. Поскольку нельзя поймать двух зайцев сразу, необходимо сделать выбор. Он зависит от характера самого инвестора и от его склонности к риску. Портфели, имеющие наи­меньший риск для заданной ожидаемой или наибольшую ожидае­мую доходность при заданном уровне риска, называются эффек­тивными портфелями.

Сформировать эффективный портфель — значит найти доли ка­питала х\, г = 1, п, которые следует вложить в ценные бумаги г-го ви­да, чтобы получить наименьший риск при заданной ожидаемой эф­фективности или наибольшую ожидаемую эффективность при за­данном уровне риска. То есть необходимо решить соответствующие задачи математического программирования:

Математическая формализация vo.lo; впервые оыла предложе­на Г.Марковичем в 1951 г., за что позднее он был удостоен Нобелев­ской премии в области экономики.

Проведем анализ решения данной задачи. ^ __

Пусть в результате решения найдены доли капитала х\ (i = 1, и) эффективного портфеля ._в Ее ли х\ > О, то это означает, что инвестор должен вложить долю х\ своего капитала в i-и вид ценных бумаг. Если же х\ < О, то инвестору следует взять в долг с обязателъп ном последующего возврата ценные бумаги г -го вида на сумму, ранную х\ долей своего капитала. Такое взятие в долг называется короткой

HJ5

продажей {short sale). Инвестор в таком случае рассчитывает на по­нижение курса ценных бумаг. Если взятие в долг невозможно, то в соответствии с формулами (6.18), (6.19) следует ввести дополни­тельное ограничение неотрицательности переменных, то есть

х, > i = 1, п.

Рис. 6.2. Область принятия решений по формированию портфеля

Эффективным портфелям соответствуют точки, расположенные на части АВ кривой, ограничивающей эту область. Эта часть кривой называется множеством Парето, или эффективной границей.

Через несколько лет после опубликования знаменитой статьи Г. Марковица другой американский мономист Д. Тобин (также впоследствии лауреат Нобелевской премии) исследовал вопрос о влиянии безрисковых ценных бумаг с фиксированным доходом на формирование портфеля и доказал, что одной из важнейших задач является задача правильного распределения капитала между без­рисковыми и рисковыми вложениями.

Однако при использовании изложенного выше метода возника­ет единственная проблема — получение достоверной статистичес­кой информации, необходимой для расчета эффективного портфе­ля. Эта проблема весьма актуальна для стран с развивающейся ры­ночной экономикой, то есть для стран, появившихся на постсовет­ском пространстве, где рынок ценных бумаг только начинает за­рождаться и речь пока не идет об эффективной статистике. Но даже в странах с высокоразвитым рынком ценных бумаг статистика дает информацию о периодах, предшествующих моменту принятия ре­шения по формированию портфеля.

При формировании портфеля всегда хотелось бы иметь инфор­мацию о будущих периодах инвестирования и о состоянии и пер­спективах развития заемщиков. Для получения такой информации наряду с известными аналитическими методами прогнозирования, основанными на использовании временных рядов, широко приме­няются методы экспертных оценок и основанные на них методы анализа, базирующиеся на использовании нечетких множеств.

Не нашли, что искали? Воспользуйтесь поиском по сайту: