|
|
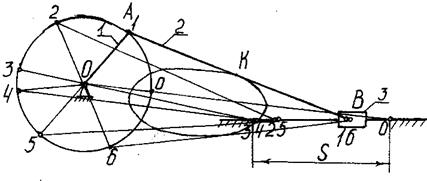
Построение положений рычажных механизмов методом засечекКинематический анализ механизмов выполняется в порядке при- соединения структурных групп. Построение положений плоских механизмов второго класса обычно выполняется методом засечек. В качестве примера рассмот- рим кривошипно-ползунный механизм (рис.14.1).
Рис. 14.1. Кривошипно-ползунный механизм
Вначале находим крайние положения механизма (0 и 3), в кото- рых кривошип 1 и шатун 2 располагаются на одной прямой. Для этого из центра О делаем засечки радиусами АВ + ОА и АB – ОА на линии движения ползуна 3. Далее делим окружность, описываемую точкой А, на равные части (например, на шесть) и отмечаем после- довательные положения точки А – 0, 1, 2, 3, 4, 5, 6, а затем методом засечек на линии движения ползуна получаем последовательные положения точки В – 0, 1, 2, 3 (движение справа налево) 4, 5, 6 (движение слева направо). S – ход ползуна. В результате получаем последовательные положения всех звеньев механизма. Траектория некоторой точки К шатуна получается, если все по- следовательные положения точки соединить плавной кривой.
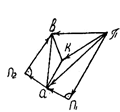
14.3. Определение скоростей и ускорений рычажных механизмов методом планов Пример 14.1.Дано: кривошипно-ползунный механизм
ω1 = 60 рад/с или n1 = 50 об/мин, lOA = 100 мм, lAB = 300 мм, ε1 =5 рад/с . Формула строения: I 0,1
а б в Рис. 14.2. К примеру 14.1
Построение плана скоростей. Скорость точки А начального звена
OA 30
μ
ω1 . Выбираем масштабный коэффициент
Рассматриваем структурную группу (2, 3). Для определения ско- рости точки B составляем векторное уравнение согласно теореме о плоскопараллельном движении:
Уравнение (14.1) решаем графически. Для этого из полюса p от-
затем из полюса p проводим прямую в направлении суммарного
лений дает точку b. В результате находим
Для определения направления угловой скорости ω2 шатуна 2
ку В и наблюдаем, в какую сторону он поворачивает звено 2 отно- сительно точки А. Скорость точки K шатуна находим на основании векторных уравнений
KB BK. В результате получим
Отметим основные свойства планов скоростей. 1. Векторы абсолютных скоростей начинаются в полюсе плана. 2. Векторы относительных скоростей соединяют концы векторов абсолютных скоростей, причем вектор на плане направлен к той
3. Теорема подобия. Отрезки относительных скоростей точек, принадлежащих одному звену, образуют фигуру, подобную соот- ветствующей фигуре звена и сходственно с нею расположенную. Сходственное расположение означает, что направления обхода од- ноименных контуров совпадают (например, а-b-k и А-В-K – по часо-
Построение плана ускорений. Ускорение точки А начального звена
t aA – касательное (тангенциальное) ускорение.
причем вектор сторону ε1 . n
Выбираем масштабный коэффициент ускорений μa, м , и
n
πn1 , мм, изображающий
aA, и отре- зок n1a мм, изображающий aA. Точка π – полюс плана ускорений. Откладываем отрезки направлениями. Тогда πn1 и n1a в соответствии с их
Рассматриваем структурную группу (2, 3). Для определения ускорения точки В составляем векторное уравнение согласно тео- реме о плоскопараллельном движении:
где aBA и aBA – нормальная и касательная составляющие ускорения
точки В во вращательном движении звена 2 относительно точ-
ки А, причем вектор aBA направлен вдоль АВ от В к А, а . Нормальная составляющая находится также по величине
n aBA
lAB
или
n aBA
Отрезок, изображающий aBA , равен
an2 n
μa
, мм.
n кладываем отрезок an2 в направлении вектора
aBA из точки n2 проводим прямую в направлении вектора aBA , а из полюса πпро-
лельно х – х. Пересечение указанных направлений дает точку b. В результате находим
lAB Для определения направления углового ускорения ε2
шатуна 2 переносим вектор касательного ускорения aBA (отрезок n2b ) в точ-
Ускорение точки K находим на основании теоремы подобия, ко- торая справедлива и для плана ускорений. Для этого методом засе- чек строим , подобный и сходственно с ним распо-
откуда Аb AB аb AB
AB AB
В результате получим
Основные свойства планов ускорений такие же, как и планов скоростей.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , механизм второго класса.
, механизм второго класса.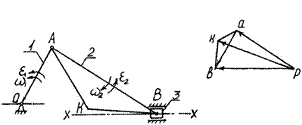
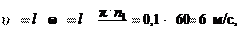 A OA 1
A OA 1
 в сторону
в сторону
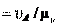
 скоростей μ и определяем отрезок pa , мм, изображаю-
скоростей μ и определяем отрезок pa , мм, изображаю-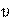 щий A. Точка p – полюс плана скоростей.
щий A. Точка p – полюс плана скоростей. (14.1)
(14.1) где – скорость точки В во вращательном движении звена 2 от-
где – скорость точки В во вращательном движении звена 2 от-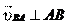
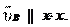 носительно точки А, ,
носительно точки А, , кладываем отрезок pa в направлении вектора , из точки a прово-
кладываем отрезок pa в направлении вектора , из точки a прово- дим прямую в направлении вектора , т. е. перпендикулярно AB,
дим прямую в направлении вектора , т. е. перпендикулярно AB,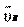 вектора , т. е. параллельно х – х. Пересечение указанных направ-
вектора , т. е. параллельно х – х. Пересечение указанных направ-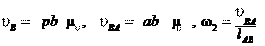

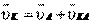
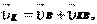 и
и
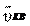
 где KA и – относительные скорости, причем ,
где KA и – относительные скорости, причем ,
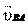 точке, которая стоит первой в индексе, например, – от а к b.
точке, которая стоит первой в индексе, например, – от а к b.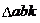
 вой стрелке). В рассмотренном примере ~ .
вой стрелке). В рассмотренном примере ~ .
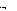 n
n
 aA направлен вдоль ОА от А к O, a в
aA направлен вдоль ОА от А к O, a в с2 мм
с2 мм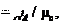 определяем отрезок
определяем отрезок t
t aA
aA (14.2)
(14.2) n t
n t aBA
aBA
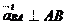 n
n BA
BA n
n
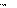 водим прямую в направлении суммарного вектора aB , т. е. парал-
водим прямую в направлении суммарного вектора aB , т. е. парал-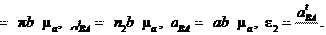
 аk AK , bk BK ,
аk AK , bk BK , аk
аk