
|
|
Условие прочности вала при совместном действии крутящего и изгибающего моментовПри ориентировочном расчете валов влияние изгиба не учиты- валось, но допускаемые напряжения на кручение принимались весьма невысокими, что должно было в известной мере компенси- ровать ошибку, являющуюся следствием пренебрежения изгибом. Применение гипотез прочности позволяет рассчитывать валы, учитывая совместное действие изгиба и кручения. При расчете валов, а также других элементов конструкций, ис- пытывающих одновременное действие изгиба и кручения, влиянием поперечных сил, как правило, пренебрегают, так как соответству- ющие им касательные напряжения в опасных точках бруса, не- велики по сравнению с касательными напряжениями от кручения и нормальными напряжениями от изгиба. На рис. 19.16, а показан вал, на который насажены зубчатое коле- со диаметром d1 и шкив ременной передачи диаметром d2 . На зуб- чатое колесо действуют окружная Ft и радиальная Fr силы, на шкив – силы F1 и F2 натяжения ветвей ремня. Для составления рас- четной схемы вала (рис. 19.16, б) все силы должны быть приведены к
к оси вала добавляется скручивающая пара с моментом M1 Ft(d1 2) (рис. 19.17, а); аналогично при при-
F1 и F2 получается скручивающая пара с моментом (рис. 19.17, б).
Рис. 19.16. Изгиб с кручением вала
Рис. 19.17. Перенос сил к оси вала
При равномерном вращении вала (только такой случай и рас-
намики для вращательного движения. На основе расчетной схемы определяют опорные реакции и строят эпюры чение вала. Mz, Mx и My, по которым определяют опасное се-
Для вала, диаметр которого по всей длине постоянен, опасным будет сечение, в котором одновременно возникают наибольшие крутящий Mz и изгибающий M и моменты. В рассматриваемом
Валы, как правило, изготовляют из среднеуглеродистой кон- струкционной или реже – легированной стали. Их расчет выполня- ют на основе третьей или пятой гипотез прочности. Составим расчетную зависимость по третьей гипотезе проч- ности. По формуле
Mи Wи 4(Mz Wp ) .
Учитывая, что для круглого (сплошного или кольцевого) сечения
Внешне эта формула аналогична расчетной зависимости для опре- деления максимальных нормальных напряжений при изгибе, поэтому величину, стоящую в числителе, называют эквивалентным (или при- веденным) моментом, при этом условие прочности имеет вид
и
Расчет бруса круглого поперечного сечения на изгиб с кру- чением ведется аналогично расчету на изгиб, но вместо изгибающе- го момента в расчетную формулу входит так называемый эквива- лентный момент, который зависит от изгибающих и крутящего моментов, а также от принятой гипотезы прочности. По гипотезе наибольших касательных напряжений,
При проектном расчете определяют требуемое значение момента сопротивления поперечного сечения:
Учитывая, что для сплошного круглого сечения W πd 3 0,1d 3 , и 32
Понятие «эквивалентный момент» не имеет смысла при изгибе с кручением бруса некруглого поперечного сечения. Неприменимо оно и в случае, если помимо изгиба и кручения брус круглого се- чения испытывает растяжение или сжатие. Для бруса с постоянным диаметром опасная точка находится в сечении, для которого эквивалентный момент имеет наибольшее значение. Это сечение также называют опасным. Для отыскания опасного сечения иногда помимо эпюр Mx, My, Mz строят эпю- ру M и , а затем эпюру M экв . Практически в этом нет необходимо- сти; в случае, если по эпюрам Mx, My, Mz положение опасного сечения определить нельзя, проще вычислить сечений, чем строить эпюры M и и M экв . Mэкв для нескольких

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 его оси. При переносе силы Ft
его оси. При переносе силы Ft ведении сил
ведении сил M2
M2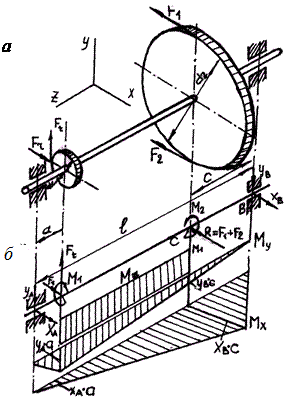
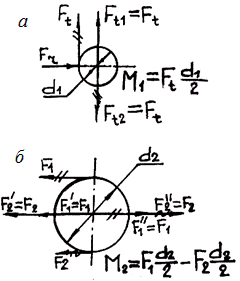
 сматривается) M1 M2 , что следует из основного уравнения ди-
сматривается) M1 M2 , что следует из основного уравнения ди-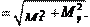 Mи
Mи σэкв
σэкв σэкв
σэкв Wp , имеем
Wp , имеем σэкв
σэкв σ
σ Mэкв
Mэкв Wи .
Wи . получаем следующую формулу для определения требуемого диа- метра вала:
получаем следующую формулу для определения требуемого диа- метра вала: d
d