
|
|
Трение качения. Работа при качении телТрением качения называется сопротивление, возникающее при перекатывании одного тела по поверхности другого. Тело 1 и каток 2 (рис. 10.9) абсолютно недеформируемые. Малая сила F вместе с си- лой трения Rf , приложенной к катку в точке K, образуют пару (F ,
Рис. 10.9. Работа сил при качении тела
ной поверхности также смещается несколько вперед на длину fkот- носительно теоретической точки касания K и отклоняется от нормали Bn на небольшой угол (рис. 10.9, в).
Rf ) с моментом F и пару сопротивления качению ( G , Rn ) с моментом Rn . Момент пары
личину fk – коэффициентом трения качения.Значение fk зави-
мер, для трения мягкой стали по стали fk = 0,005 см, а для трения закаленной стали по стали (подшипники качения) Качение катка 2 начинается при условии fk = 0,001 см.
Для перекатывания катка сила
r ГЛАВА 11. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ Импульс силы. Количество движения. Кинетическая энергия Любое взаимодействие тел, приводящее к какому-либо измене- нию движения, длится некоторое время. Векторная мера действия
ток времени ее действия, называется элементарным импульсом силы. Направление вектора импульса совпадает с направлением вектора силы. Единица импульса в СИ – Н ∙ с:
с2 с 1 кг м . с
Единица количества движения в СИ – кг м . Как видим, единицы с импульса силы и количества движения одинаковы. Скалярная мера механического движения точки , равная
половине произведения массы точки на квадрат ее скорости, назы- вается кинетической энергией. Единица кинетической энергии – джоуль (Дж):
1 Дж 1 Н м 1 м 1 . с2 с2
Теорема об изменении количества движения точки
(изменение количества движения точки равно импульсу всех сил). Спроецировав на оси координат обе части векторного равен- ства (11.1), в общем случае получим: а) систему трех скалярных уравнений:
Fkx; F y Fky; F z Fkz;
в) если силы действуют вдоль одной прямой, то, спроецировав уравнение (11.1) на эту прямую, получим одно скалярное уравнение:
11.3.
На прямолинейном пути
т. е. изменение кинетической энергии точки равно сумме работ дей- ствующих сил.
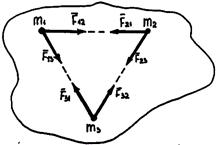
Понятие о механической системе Совокупность материальных точек, связанных между собой си- лами взаимодействия, называется механической системой (рис. 11.1). Например, механическую систему образуют Земля и Луна или спортивный самолет и буксируемый им планер. Любое материальное тело рассматривается в механике как меха- ническая система, образуемая совокупностью материальных точек. Абсолютно твердое тело носит название неизменяемой механической системы, так как расстояние между материальными точками остается неизменным. Изменяемые системы – любые машины или механизмы.
И т.д. F21 F32 F13
Рис. 11.1. К понятию о механической системе
Если рассматривать какую-либо механическую систему, то силы, действующие на точки системы со стороны точек или тел, не входя- щих в эту систему, называются внешними (Fe, Re), а силы, дей- ствующие на точки системы со стороны точек или тел этой же сис- темы, называются внутренними (Fi). Главный вектор всех внутренних сил механической системы ра- вен нулю, причем это условие соблюдается, только если рассматри- ваемая механическая система неизменяемая. Движение механической системы зависит: 1) от действующих сил; 2) суммарной массы системы
mk– массы ее отдельных точек; 3) положения центра масс системы.
 Движение центра масс определяется (только при поступательном движении) уравнением Движение центра масс определяется (только при поступательном движении) уравнением
где Fс – результирующая всех внешних сил, приложенных к точ-
m – масса системы;
Как видим, это уравнение аналогично основному уравнению ди- намики точки. Смысл его состоит в том, что центр масс системы движется как материальная точка, в которой сосредоточена масса всей системы и приложены все внешние силы.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 Rf), под действием которой каток начинает катиться (рис. 10.9, а).
Rf), под действием которой каток начинает катиться (рис. 10.9, а).

 На самом деле абсолютно недеформируемых тел нет (рис. 10.9, б). При перекатывании катка силой F деформация смещается вперед по направлению качения и место приложения полной реакции R опор-
На самом деле абсолютно недеформируемых тел нет (рис. 10.9, б). При перекатывании катка силой F деформация смещается вперед по направлению качения и место приложения полной реакции R опор-

 При качении катка на него действуют четыре силы, образующие
При качении катка на него действуют четыре силы, образующие
 две пары сил: движущую пару ( F ,
две пары сил: движущую пару ( F , сопротивления иначе называют моментом трения качения, а ве-
сопротивления иначе называют моментом трения качения, а ве- сит от материала тел и выражается обычно в сантиметрах. Напри-
сит от материала тел и выражается обычно в сантиметрах. Напри- F
F F
F силы F dt , равная произведению силы на элементарный промежу-
силы F dt , равная произведению силы на элементарный промежу- 1 Н с 1 кг м
1 Н с 1 кг м Векторная мера механического движения точки
Векторная мера механического движения точки  , равная произведению массы точки на ее скорость в данный момент време- ни, называется количеством движения. Направление вектора ко- личества движения совпадает с направлением вектора скорости.
, равная произведению массы точки на ее скорость в данный момент време- ни, называется количеством движения. Направление вектора ко- личества движения совпадает с направлением вектора скорости. 2
2 кг м кг м2
кг м кг м2
 Пусть на точку массой m действует система постоянных сил, рав- нодействующая которых F согласно основному закону динамики
Пусть на точку массой m действует система постоянных сил, рав- нодействующая которых F согласно основному закону динамики
 так как (11.1)
так как (11.1)
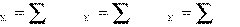 где F x
где F x

 Пусть на точку действует система постоянных сил, равнодейст- вующая которых F . Допустим, что силы действуют вдоль одной прямой. Тогда
Пусть на точку действует система постоянных сил, равнодейст- вующая которых F . Допустим, что силы действуют вдоль одной прямой. Тогда
 a
a
 Отсюда с учетом того, что F S W Wk,
Отсюда с учетом того, что F S W Wk, ,
, F12 F23 F31
F12 F23 F31 m ,
m , где m – масса механической системы;
где m – масса механической системы;

