
|
|
Классификация напряженных состоянийНапряженное состояние в данной точке тела характеризуется со- вокупностью нормальных и касательных напряжений, возникаю- щих на бесчисленном множестве различно ориентированных в про- странстве площадок, которые можно провести через эту точку. Предположим, что в окрестности исследуемой точки выделен бес- конечно малый элемент, имеющий форму прямоугольного паралле- лепипеда, и напряжения, возникающие на его гранях, известны. Девять величин называют компонентами (рис. 17.1) напряженно- го состояния в данной точке. Из условия равновесия выделенного элемента следует, что со- ставляющие касательных напряжений, возникающих на любых двух взаимно перпендикулярных площадках, перпендикулярные общему ребру этих площадок, равны по абсолютному значению, т. е.
Рис. 17.1. Напряжения на гранях элементарного куба
Это положение называют законом парности касательных напряжений. Следовательно, из девяти компонентов напряженного состояния независимы лишь шесть. Первое положение теории напряженного состояния может быть сформулировано следующим образом: напряженное состояние в точке тела задано, если известны напряжения на любых трех прохо- дящих через нее взаимно перпендикулярных площадках. Среди бесчисленного множества площадок, которые можно про- вести через исследуемую точку, имеются три взаимно перпендику- лярные площадки, касательные напряжения на которых отсутству- ют. Эти площадки и возникающие на них нормальные напряжения называют главными. Классификацию видов напряженного состояния ведут по глав- ным напряжениям. Если все три главных напряжения отличны от нуля, напряженное состояние называют объемным, простран- ственным или трехосным. В случае если одно из главных напря- жений равно нулю, напряженное состояние называют плоским, или двухосным, наконец, если лишь одно из главных напряжений от- лично от нуля, напряженное состояние линейное, или одноосное:
– плоское; – линейное.
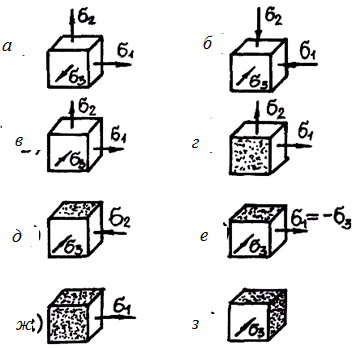
Элементы, выделенные главными площадками, для различных частных случаев напряженного состояния показаны на рис. 17.2: а – трехосное растяжение; б – трехосное сжатие; в – трехосное сме- шанное напряженное состояние; г – двухосное растяжение; д – двухосное сжатие; е – частный случай двухосного смешанного напряженного состояния – чистый сдвиг; ж – одноосное растяже- ние; з – одноосное сжатие. Площадки, свободные от напряжений, так называемые нулевые главные площадки, покрыты точками.
Рис. 17.2. Различные случаи напряженного состояния 17.2.
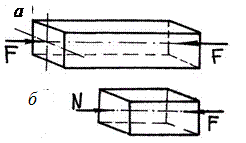
При растяжении (сжатии) прямого бруса в его поперечных сече- ниях возникает только один внутренний силовой фактор – продоль- ная сила, обозначаемая Nz или N (рис. 17.3, 17.4).
Рис. 17.3. Однородное сжатие бруса
Рис. 17.4. Однородное растяжение бруса
Прямые брусья, работающие на растяжение или сжатие, часто называют стержнями. Продольные силы, соответствующие деформации растяжения, условимся считать положительными, а сжатия – отрицательными. При растяжении продольная сила направлена от сечения (рис. 17.4, б), а при сжатии – к сечению (рис. 17.3, а). Модуль и направление (знак) продольной силы определяются из уравнения равновесия, составленного для отсеченной (оставленной после проведения сечения) части бруса:
откуда
ост. части N
ост.
ост. части
Продольной силой в поперечном сечении бруса называется рав- нодействующая внутренних нормальных сил, возникающих в этом сечении:
В тех случаях когда продольные силы в различных поперечных сечениях бруса неодинаковы, закон их изменения по длине бруса удобно представить в виде графика, называемого эпюрой продоль- ных сил.
Эпюру продольных сил строят в первую очередь для того, чтобы использовать ее при расчете бруса на прочность. Напряжения.При растяжении (сжатии) бруса в его поперечных сечениях возникают только нормальные напряжения(рис. 17.5):
A
В тех случаях когда нормальные напряжения в различных попе- речных сечениях бруса неодинаковы, целесообразно показывать закон их изменения по длине бруса в виде графика – эпюры нор- мальных напряжений. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
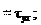
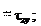

 τxy τyz τzx
τxy τyz τzx




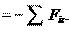 N
N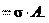 N
N Эпюра продольных сил – это график функции N .
Эпюра продольных сил – это график функции N . σ
σ Рис. 17.5. Нормальные напряжения
Рис. 17.5. Нормальные напряжения
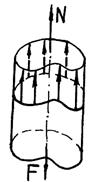 Рис. 17.6. Местные напряжения
Рис. 17.6. Местные напряжения