
|
|
Кинематические и геометрические параметры передачи.Движение ремня по шкиву сопровождается упругим скольжением. Причину этого явления можно понять из рассмотрения деформа- ции упругого ремня на заторможенном шкиве. Предположим, что к обоим концам ремня подвешены одинаковые грузы, создающие в ремне силы F1 (рис. 23.6, а). В результате между шкивом и ремнем возникнут некоторые контактные давления, а спадающие ветви ремня получат относительные удлинения
где Е ∙ A – жесткость сечения ремня при растяжении.
Рис. 23.6. Схемы деформаций ремня на шкиве
Если теперь на одном конце, например, правом, несколько уменьшить груз и тем самым силу в ветви до значения F2 (рис. 23.6, б), то относительное удлинение правого конца умень- шится до значения ε F2 , а относительное удлинение левого
конца останется прежним. Относительное сокращение длины
ремня по дуге обхвата от точки С к точке А, вызывая скольжение ремня по шкиву справа налево. Так как ремень прижат к шкиву, то скольжение вызовет силы трения qf, направленные навстречу отно- сительному скольжению. Скольжение ремня и изменение деформа- ций прекратятся в некоторой точке В дуги обхвата. Ее положение можно определить из равенства разности сил F1 и F2 суммарной си- ле трения. На дуге ВА ремень будет находиться в покое. Сумма длин дуг АВ и ВС равна длине дуги обхвата шкива ремнем (АС), определяемой углом обхвата α. Угол αc, соответствующий дуге ВС, называют углом скольжения. По мере уменьшения силы F2 (или увеличения силы F1) дуга упругого скольжения растет за счет уменьшения дуги покоя. Так как скольжение ремня связано с его упругими свойствами, то его называют упругим. Полезная нагрузка (окружная сила) Ftпередачи, развиваемая в основном за счет сил трения на дуге скольжения:
F F F 2T1 ,
где F1 – сила натяжения ведущей ветви, набегающей на ведущий шкив; F2 – сила натяжения ведомой ветви, сбегающей с ведущего шкива; T1 – вращающий момент; d1 – диаметр ведущего шкива. Положение точки В на шкиве также зависит от нагрузки и усло- вий трения.
вой скоростью ω1 его окружная скорость (здесь
ε
i В расчетах на основании экспериментов принимают ε = 0,01 – для плоскоременных передач; ε = 0,015–0,020 – для клиноременных передач. Основные геометрические параметры.Минимальное межосе- вое расстояние в плоскоременных передачах
В клиноременных передачах (на основании практики)
а максимальное межосевое расстояние
Требуемая длина ремня для передачи при заданном (или жела- тельном) межосевом расстоянии a и угле обхвата α определяется как сумма прямолинейных участков и дуг обхвата:
2 4a Угол обхвата меньшего шкива
23.3. Начальное натяжение ремня – необходимое условие работы ре- менной передачи. Сила Fнач (начального натяжения ремня) вызыва- ет в его ветвях силы
где γ – угол наклона ветви ремня к линии центров передачи. При действии вращающего момента T1 силы в ветвях будут равны F1 и F2 (рис. 23.7).
Рис. 23.7. Силы натяжения ветвей ремня
Напряжения в сечениях ведущей и ведомой ветвей ремня от начального натяжения
и при действии внешней нагрузки
где А – площадь поперечного сечения ремня. Наибольшие напряжения испытывают наружные волокна в зоне контакта ремня с малым шкивом. Здесь к основным растягивающим напряжениям σ1 от полезной нагрузки добавляются дополнительные напряжения растяжения σц и σи соответственно от центробежных сил и изгиба ремня (как стержня) вокруг шкива (рис. 23.8), следова- тельно,
Рис. 23.8. Распределение напряжений в ремне
T1 где ψ – коэффициент тяги. (23.1)
сила натяжения F1 ведущей ветви под нагрузкой и существенно снижается долговечность ремня. Для получения высокой тяговой способности передач с плоским ремнем рекомендуется обеспечивать α ≥ 150º. Благодаря хорошему сцеплению ремня со шкивом клиноремен- ные передачи хорошо работают при углах обхвата α ≥ 120º. Коэффициент тяги
2F0
Экспериментально установлено, что коэффициенты тяги ψ и упругого скольжения ремня ε взаимосвязаны (кривая скольжения, рис. 23.9).
Рис. 23.9. Кривая скольжения и зависимость КПД от коэффициента тяги в клиноременной передаче
КПД передач.При работе плоскоременной передачи часть энер- гии расходуется на упругий гистерезис при циклическом деформи- ровании ремня (растяжение, сдвиг, изгиб), на скольжение ремня по шкивам, аэродинамическое сопротивление движению ремня и шки- вов, а также трение в подшипниках валов передачи. В клиноременной передаче к этим потерям добавляются потери на трение при радиальном перемещении ремня в процессе его входа в канавку и выхода из нее. КПД ременной передачи
зависит от коэффициента тяги ψ (см. соотношение (23.1)) и соот- ветствующего ему коэффициента относительного скольжения рем- ня ε (см. рис. 23.9). Наибольший КПД соответствует некоторому значению ψ0 на линейном участке кривой скольжения. Когда
При оптимальной нагрузке η = 0,97–0,98 для плоскоременной передачи и 0,92–0,97 – для клиноременной. Главные критерии работоспособности передачи.Опыт эксп- луатации ременных передач показал, что их работоспособность ограничена тяговой способностью и долговечностью ремня. Расчет ременных передач на тяговую способность основан на показателях тяговой способности и долговечности. Для расчета используют условие работоспособности передачи в виде
где σt– удельная окружная сила, называемая полезным напряжением; A – площадь поперечного сечения ремня (комплекта ремней); σt – допускаемое полезное напряжение. Удельная окружная сила σt– параметр, характеризующий тяго- вую способность передачи. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ε1 ,
ε1 ,

 2 E A
2 E A ( ε1 ε2 ) элемента правой спадающей ветви распространится вдоль
( ε1 ε2 ) элемента правой спадающей ветви распространится вдоль
 Кинематика передачи. При вращении ведущего шкива с угло-
Кинематика передачи. При вращении ведущего шкива с угло-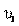

 . Коэффициент упругого скольжения
. Коэффициент упругого скольжения Передаточное отношение
Передаточное отношение amin
amin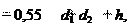 amin
amin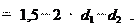 amax
amax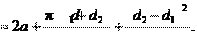 l
l α1
α1 F0
F0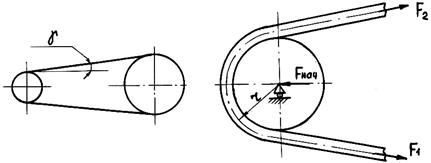
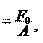 σ0
σ0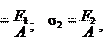 σ1
σ1 σ1max
σ1max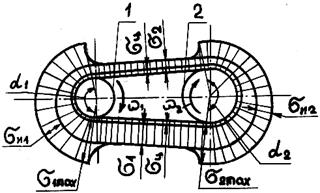
 Фактическую тяговую способность передачи характеризует окружная сила Ftили вращающий момент T1, который может раз- вить ведущий шкив:
Фактическую тяговую способность передачи характеризует окружная сила Ftили вращающий момент T1, который может раз- вить ведущий шкив: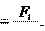 ψ
ψ
 η
η
 σt (23.2)
σt (23.2)