
|
|
Кинематика зубчатых механизмов с подвижными осями вращенияЗубчатая передача, у которой геометрическая ось хотя бы одного из колес подвижна, называется планетарной. Различные плане- тарные механизмы можно представить в виде трех типов передач. 1. Дифференциальные передачи, обладающие двумя степенями подвижности, у которых все основные звенья подвижны (рис. 15.6). Эти передачи позволяют суммировать два или несколько потоков мощности, поступающих от независимых источников, либо распре- делять их по независимым потребителям.
Рис. 15.6. Дифференциальная передача 2.
Рис. 15.7. Планетарная передача
3. Замкнутые дифференциальные передачи, получаемые из диф- ференциальных передач путем замыкания двух основных звеньев (центрального колеса и водила) простой передачей, состоящей из колес 1, 2, 3 (рис. 15.8). Такие передачи позволяют получить боль- шие передаточные отношения при малых габаритах.
Рис. 15.8. Замкнутая дифференциальная передача Рассмотрим механизм, изображенный на рис. 15.6. Определим число степеней подвижности, если n = 4 – число звеньев, p5 = 4 и p4 = 2 – число кинематических пар V и IV класса. Определенность в движении звеньев у этого механизма будет в том случае, если будут заданы законы движения двум звеньям. Основными звеньями механизмов с подвижными осями являют- ся водило (Н) и соосные с ним колёса (1 и 3). В данном случае все основные звенья подвижные. Оба эти признака (W > 1 и подвижные основные звенья) определяют дифференциальный механизм. Определим степень подвижности для механизма, изображенного на рис. 15.7:
У этого механизма колесо 3 (основное звено) неподвижно и W = 1. Оба признака определяют планетарный механизм. В меха- низмах замкнутых дифференциалов все основные звенья подвиж- ные но число степеней подвижности равно единице (W = 1). Таким образом, только по совокупности двух признаков механизмы с по- движными осями можно отнести к тому или иному типу. Формулы (15.1), (15.2) для определения передаточного отноше- ния планетарных и дифференциальных механизмов использовать нельзя, так как сателлит участвует в сложном движении, состоящем из вращения вокруг оси O2 и вращения вместе с водилом Н вокруг оси Он (см. рис. 15.6, 15.7). Для вывода зависимостей, связывающих угловые скорости меха- низмов, имеющих подвижные оси, воспользуемся методом обраще- ния движения. Допустим, что в действительном движении звенья механизма (см. рис.15.6) имеют угловые скорости ω1, ω2 , ω3 и ω4 . Сообщим
), то мы получили
ω3
– передаточное отношение «обращенного механизма», кото- рое можно определить через число зубьев колес:
z1
В правую часть предыдущей зависимости подставим значение относительных скоростей:
Полученное уравнение называется формулой Виллиса для диф- ференциальных механизмов. Левая часть, как показано выше, мо- жет быть выражена через число зубьев колес. Определенность в решении правой части будет иметь место, когда будут известны скорости двух ведущих звеньев. Установим, какой вид примет фор- мула Виллиса для планетарного механизма, изображенного на рис. 15.7. У этого механизма колесо 3 жестко соединено со стойкой
Таким образом, имеем
i1H
(15.4) Полученную зависимость называют формулой Виллиса для планетарных механизмов, а передаточное отношение тарным передаточным отношением. i1H – плане-
рез число зубьев колес. В общем случае определяется че-
где ikH– передаточное отношение от звена k к звену l (l соответ- ствует неподвижному центральному колесу). Достоинством планетарных механизмов является возможность получения больших передаточных отношений при малых габаритах. Пример 15.1. Определить передаточное отношение iH1 планетар-
Рис. 15.9. К примеру 15.1
Это одноступенчатый планетарный редуктор. Используя форму- лу (15.4), запишем
H 1
рость ω = 340 с–1 и постоянное угловое ускорение ε1 = 285 с ,
z1 = z2 = 18; z2´ = z4´ = 18; z3 = z5 = 30; z3´ = z5´ = 22; z4 = z6 = 70.
Рис. 15.10. К примеру 15.2
Принять средний модуль конического колеса mm= 2 мм, ширину колеса b = 20 мм, плотность ρ = 8000 кг/м, смещение центра масс (точки А, рис. 15.11) l = 2 мм.
Рис. 15.11. Смещение центра масс
1) передаточное отношение между входным и выходным звень- ями и направление вращения; 2) угловую скорость и угловое ускорение выходного звена, их направление показать на схеме передачи; 3) время, в течение которого угловая скорость увеличится в два раза; 4) величину и направление силы инерции и момента пары сил инерции звена 1 в начале и конце найденного в предшествующем пункте промежутка времени, сравнить силу инерции с силой тяже- сти и показать на чертеже направления вращения, ускорения и инерционных нагрузок; 5) общий коэффициент полезного действия передачи.
Решение 1. Определение передаточного отношения механизма.
ω7 ωH Выделим из механизма ступень с неподвижными осями, состоя- щую из колес z1, z2, z2´, z3 , z3´, z4, и планетарную ступень, состоящую из колес z4´, z5, z5´, z6 и водила Н (7); а) для ступени с неподвижными осями
i14
б) чтобы определить передаточное отношение планетарной сту- пени, используем формулу Виллиса; остановим водило Н (7), ис- пользуя зависимость (15.3), получим
колесо 6 неподвижно ( ω6 = 0), используя зависимость (15.4), получим
в) передаточное отношение всего механизма
Передаточное отношение планетарной ступени i4 H 1. . Сле-
ε7 на чертеже стрелками. Поскольку ε1 0 , вращение ускоренное. 2. Угловая скорость и угловое ускорение ведомого звена 7 по модулю:
3. Определить время, в течение которого угловая скорость уве-
Отсюда t ω1 ω1 ε1 2ω1 ω1 ε1 ω1 340 1,19 c. ε1 285 4. Для расчета момента инерции I01 коническое ведущее колесо
С учетом сказанного масса определяется по формуле
где ρ – плотность, ρ = 8000 кг/м3 (по условию).
1 0,163 0, 0362 2, 64 10 5 кг м2.
Вес колеса
Нормальное ускорение точки A
Касательное ускорение точки A и касательная составляющая си- лы инерции:
Определим полное ускорение точки А, силу инерции и направ- ление силы инерции:
A
tgα
37, 7
F τ , как малой вели- чиной, можно пренебречь и считать, что ним силу тяжести и силу инерции: Fин Срав-
G 1, 6
Силой веса по сравнению с силой инерции при практических расчетах также можно пренебречь. Момент сил инерции
Покажем направление всех векторных величин на чертеже. 5. Определение общего КПД механизма.
Здесь ηк – КПД конической пары с учетом потерь в
ηпл – КПД цилиндрической пары (две пары по условию); –

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|

 Простые планетарные передачи, обладающие одной степенью подвижности, у которых одно из основных звеньев закреплено неподвижно (рис. 15.7, закреплено звено 3). Такие механизмы слу- жат для последовательной передачи потока мощности.
Простые планетарные передачи, обладающие одной степенью подвижности, у которых одно из основных звеньев закреплено неподвижно (рис. 15.7, закреплено звено 3). Такие механизмы слу- жат для последовательной передачи потока мощности.

 W
W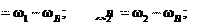
 \
\ «обращенный механизм» с неподвижными осями. Для этого меха- низма справедлива зависимость
«обращенный механизм» с неподвижными осями. Для этого меха- низма справедлива зависимость


 (заторможено), т. е. ω3 .
(заторможено), т. е. ω3 .

 ikH ,
ikH ,
 i
i

 i17
i17 i14
i14
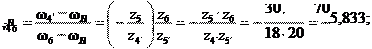

 i17
i17
 довательно, водило Н (7) вращается в ту же сторону, что и колесо 4. Покажем направление угловой скорости ω7 и углового ускорения
довательно, водило Н (7) вращается в ту же сторону, что и колесо 4. Покажем направление угловой скорости ω7 и углового ускорения
 ω7
ω7
 ε
ε личивается вдвое: ω1 2ω1.
личивается вдвое: ω1 2ω1. Для ускоренного вращения ω1 ω1 εt .
Для ускоренного вращения ω1 ω1 εt .
 m1 4 1 4
m1 4 1 4 I 1 m r2
I 1 m r2 G
G Смещение центра масс (точка А на рис. 15.11) l = 2 мм = 0,002 м. Нормальная составляющая силы инерции
Смещение центра масс (точка А на рис. 15.11) l = 2 мм = 0,002 м. Нормальная составляющая силы инерции an .
an . A 1 с2
A 1 с2
 aA 1 с2 ;
aA 1 с2 ; a
a Fин
Fин Fин
Fин
 Fин 37, 7 23, 6.
Fин 37, 7 23, 6. Mu
Mu η = ηк
η = ηк подшипниках.
подшипниках. КПД планетарной передачи.
КПД планетарной передачи. η
η