
|
|
Пространственная система произвольно расположенных сил. Условие равновесияРанее подробно был изложен процесс приведения сил к точке и доказано, что любая плоская система сил приводится к силе – глав- ному вектору – и паре, момент которой называется главным момен- том, причем эквивалентные данной системе сил сила и пара дей- ствуют в той же плоскости, что и заданная система. Значит, если главный момент изобразить в виде вектора, то главный вектор и главный момент плоской системы сил всегда перпендикулярны друг другу.
Векторные равенства Fгл и Mгл выражают необходимое
Если главный вектор равен нулю, то его проекции на три взаим- но перпендикулярные оси также равны нулю. Если главный момент равен нулю, то равны нулю и три его составляющие на те же оси:
Значит, произвольная пространственная система сил статически определима лишь в том случае, когда число неизвестных не превы- шает шести. Среди задач статики часто встречаются такие, в которых на тело действует пространственная система параллельных друг другу сил (рис. 5.6).
Рис. 5.6. Пространственная система параллельных сил Уравнения равновесия для пространственной системы парал- лельных сил:
В пространственной системе параллельных сил неизвестных должно быть не больше трех, иначе задача становится статически неопределимой.
ГЛАВА 6. КИНЕМАТИКА ТОЧКИ Основные понятия кинематики Раздел механики, занимающийся изучением движения матери- альных тел без учета их масс и действующих на них сил, называется кинематикой. Движение – основная форма существования всего материально- го мира, покой и равновесие – частные случаи.
Все тела состоят из материальных точек. Чтобы получить пра- вильное представление о движении тел, начинать изучение нужно с движения точки. Перемещение точки в пространстве выражается в метрах, а также в дольных (см, мм) или кратных (км) единицах дли- ны, время – в секундах. В практике или жизненных ситуациях вре- мя часто выражают в минутах или часах. Отсчет времени при рас- смотрении того или иного движения точки ведут от определенного, заранее обусловленного начального момента (t = 0). Геометрическое место положений движущейся точки в рассмат- риваемой системе отсчета называется траекторией. По виду тра- ектории движение точки делится на прямолинейное и криволиней- ное. Траектория точки может быть определена и задана заранее. Так, например, траектории искусственных спутников Земли и меж- планетных станций вычисляют заранее, или если принять движу- щиеся по городу автобусы за материальные точки, то их траектории (маршруты) также известны. В подобных случаях положение точки в каждый момент времени определяется расстоянием (дуговой ко- ординатой) S, т. е. длиной участка траектории, отсчитанной от неко- торой ее неподвижной точки, принятой за начало отсчета. Отсчет расстояний от начала траектории можно вести в обе стороны, по- этому отсчет в одну какую-либо сторону условно принимают за по- ложительный, а в противоположную – за отрицательный, т. е. рас- стояние S – величина алгебраическая. Она может быть положитель- ной (S > 0) или отрицательной (S < 0). При движении точка за определенный промежуток времени про- ходит некоторый путь L, который измеряется вдоль траектории в направлении движения (рис. 6.1):
Если точка стала двигаться не из начала отсчета O, а из поло- жения, находящегося на начальном расстоянии S0, то
Рис. 6.1. Движение точки
Векторная величина, характеризующая в каждый данный момент времени направление и быстроту движения точки, называется ско- ростью. Единицы скорости:
ч 3600 с с
Скорость точки в любой момент ее движения направлена по ка- сательной к траектории (рис. 6.2):
Рис. 6.2. Вектор скорости точки Отметим, что это векторное равенство характеризует лишь по-
где AA1 – путь, пройденный точкой за время .
Векторная величина, характеризующая быстроту изменения направления и числового значения скорости, называется ускоре- нием (рис. 6.3):
Рис. 6.3. Ускорение точки
При равномерном движении по криволинейной траектории точка тоже имеет ускорение, так как и в этом случае изменяется направ- ление скорости (рис. 6.4):
Рис. 6.4. К определению ускорения точки
с2
6.2. Способы задания движения точки Существует три способа задания движения: естественный, коор- динатный, векторный. Естественный способ задания движения точки. Если кроме траектории, на которой отмечено начало отсчета O, задана зависи-
называется законом движения точки по заданной траектории (рис. 6.5).
Пусть, например, задана некоторая траектория, движение точки
счета O; в момент времени
t1 1 c точка находится на расстоянии
0,5 1 0,5 м ; в момент времени t2 точка нахо- дится на расстоянии S2 0,5t2 0,5 22 2 м от начала отсчета O.
Рис. 6.6. Координатный способ задания движения точки
Эти уравнения выражают закон движения точки в прямо- угольной системе координат (OXYZ). В частном случае, если точка движется в плоскости, закон дви-
Пример 6.1.Движение точки в плоской системе координат зада-
начале координат; в момент времени t1 1 c координаты точки
3t1 3 1 3 см ; в момент времени t2
2t2 2 2 4 см , Y2 3t2 3 2 6 см и т. д.
Рис. 6.7. К примеру 6.1
Зная закон движения точки в прямоугольной системе координат, можно определить уравнение траектории точки.
, получим уравнение траектории 3x . Как

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|

 и достаточное условие равновесия пространственной системы про- извольно расположенных сил.
и достаточное условие равновесия пространственной системы про- извольно расположенных сил.


 S1 .
S1 . L .
L .
 км 103 м
км 103 м

 1 = .
1 = .



 ложение , а модуль средней скорости за время
ложение , а модуль средней скорости за время


 .
.
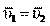

 За единицу ускорения принимают обычно 1 м .
За единицу ускорения принимают обычно 1 м . мость S между расстоянием S и временем t, это уравнение
мость S между расстоянием S и временем t, это уравнение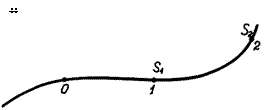 Пример: S 0,5t.
Пример: S 0,5t. Рис. 6.5. Траектория движения точки
Рис. 6.5. Траектория движения точки
 по которой определяется уравнением S S . Тогда
по которой определяется уравнением S S . Тогда
 в момент времени t0 S0 0 , т. е. точка находится в начале от-
в момент времени t0 S0 0 , т. е. точка находится в начале от- 2 2
2 2
 пликатой Z (рис. 6.6): X или, исключив
пликатой Z (рис. 6.6): X или, исключив время, Ф(X ,Y, Z) .
время, Ф(X ,Y, Z) .
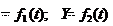 жения точки выражается двумя уравнениями: X
жения точки выражается двумя уравнениями: X или Ф(X ,Y ) .
или Ф(X ,Y ) .
 но уравнениями X и Y (X и Y – см, t – с) (рис. 6.7). Тогда
но уравнениями X и Y (X и Y – см, t – с) (рис. 6.7). Тогда
 в момент времени t0 и Y0 0 , т. е. точка находится в
в момент времени t0 и Y0 0 , т. е. точка находится в X1 , Y1
X1 , Y1

 Например, исключив время t из заданных выше уравнений
Например, исключив время t из заданных выше уравнений X и Y
X и Y